网络流
匈牙利

#include<cstdio> #include<cstring> #include<algorithm> #include<cmath> #include<vector> #define LL long long using namespace std; const int MAXN = 1e3 + 10, INF = 1e9 + 10; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } vector<int> v[MAXN]; int N, M, E; int link[MAXN], vis[MAXN], cur = 1; int Aug(int x) { for(int i = 0; i < v[x].size(); i++) { int to = v[x][i]; if(vis[to] == cur) continue; vis[to] = cur; if(!link[to] || Aug(link[to])) { link[to] = x; return 1; } } return 0; } main() { #ifdef WIN32 freopen("a.in", "r", stdin); //freopen("b.out", "w", stdout); #endif int N = read(), M = read(), E = read(); for(int i = 1; i <= E; i++) { int x = read(), y = read(); if(x <= N && y <= M) { v[x].push_back(y); //v[y].push_back(x); } } int ans = 0; for(int i = 1; i <= N; i++, cur++) if(Aug(i)) ans++; printf("%d ", ans); return 0; }
Dinic

// luogu-judger-enable-o2 #include<cstring> #include<cstdio> #define add_edge(x, y, z) AddEdge(x, y, z); AddEdge(y, x, 0); #define min(x, y) x < y ? x : y #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1 << 19, stdin), p1 == p2) ? EOF : *p1++) #define rg register const int MAXN = 10001, INF = 1e9 + 10; char buf[1 << 19], *p1 = buf, *p2 = buf; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9'){if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M, S, T; struct node { int u, v, f, nxt; }E[200002]; int head[MAXN], cur[MAXN], num = 0, deep[MAXN], vis[MAXN], q[MAXN]; inline void AddEdge(int x, int y, int z) { E[num] = (node){x, y, z, head[x]}; head[x] = num++; } inline bool BFS() { int l = 1, r = 1; q[r++] = S; memset(deep, 0, sizeof(deep)); deep[S] = 1; while(l < r) { int p = q[l++]; for(rg int i = head[p]; i != -1; i = E[i].nxt) { if(E[i].f && !deep[E[i].v]) { deep[E[i].v] = deep[p] + 1; if(E[i].v == T) return deep[T]; q[r++] = E[i].v; } } } return deep[T]; } int DFS(int x, int flow) { if(x == T) return flow; int ansflow = 0; for(rg int &i = cur[x]; i != -1; i = E[i].nxt) { if(deep[E[i].v] == deep[x] + 1 && E[i].f) { int canflow = DFS(E[i].v, min(E[i].f, flow)); flow -= canflow; E[i].f -= canflow; E[i ^ 1].f += canflow; ansflow += canflow; if(flow <= 0) break; } } return ansflow; } inline int Dinic() { int ans = 0; while(BFS()) { memcpy(cur, head, sizeof(head)); ans += DFS(S, INF); } return ans; } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif memset(head, -1, sizeof(head)); N = read(); M = read(); S = read(); T = read(); for(rg int i = 1; i <= M; i++) { rg int x = read(), y = read(), z = read(); add_edge(x, y, z); } printf("%d", Dinic()); return 0; }
最小费用最大流

// luogu-judger-enable-o2 /* */ #include<cstdio> #include<algorithm> #include<cstring> #include<queue> using namespace std; const int MAXN = 1e5 + 10, INF = 1e9 + 10; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = 1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M, S, T; struct Edge { int u, v, w, f, nxt; }E[MAXN]; int head[MAXN], num = 0; inline void AddEdge(int x, int y, int w, int f) { E[num] = (Edge){x, y, w, f, head[x]}; head[x] = num++; } int anscost, ansflow, dis[MAXN], vis[MAXN], Pre[MAXN]; bool SPFA() { memset(dis, 0x3f, sizeof(dis)); memset(vis, 0, sizeof(vis)); queue<int> q; q.push(S); dis[S] = 0; while(!q.empty()) { int p = q.front(); q.pop(); vis[p] = 0; for(int i = head[p]; i !=- 1; i = E[i].nxt) { int to = E[i].v; if(dis[to] > dis[p] + E[i].w && E[i].f) { dis[to] = dis[p] + E[i].w; Pre[to] = i; if(!vis[to]) q.push(to), vis[to] = 1; } } } return dis[T] <= INF; } int F() { int nowflow = INF; for(int i = T; i != S; i = E[Pre[i]].u) nowflow = min(nowflow, E[Pre[i]].f); for(int i = T; i != S; i = E[Pre[i]].u) E[Pre[i]].f -= nowflow, E[Pre[i] ^ 1].f += nowflow; anscost += dis[T] * nowflow; ansflow += nowflow; } void MCMF() { while(SPFA()) F(); } int main() { memset(head, -1, sizeof(head)); N = read(); M = read(); S = read(); T = read(); for(int i = 1; i <= M; i++) { int x = read(), y = read(), f = read(), w = read(); AddEdge(x, y, w, f); AddEdge(y, x, -w, 0); } MCMF(); printf("%d %d", ansflow, anscost); return 0; } /* */
图论
最短路
SPFA

1 #include<cstdio> 2 #include<queue> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=1000001; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 13 struct node 14 { 15 int u,v,w,nxt; 16 }edge[MAXN]; 17 int head[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y,int z) 20 { 21 edge[num].u=x; edge[num].v=y; 22 edge[num].w=z; edge[num].nxt=head[x]; 23 head[x]=num++; 24 } 25 int N,M,S=1;; 26 int dis[MAXN],vis[MAXN]; 27 inline void SPFA() 28 { 29 queue<int>q;q.push(S); 30 while(q.size()!=0) 31 { 32 int p=q.front(); 33 q.pop();vis[p]=0; 34 for(int i=head[p];i!=-1;i=edge[i].nxt) 35 if(dis[edge[i].v]>dis[edge[i].u]+edge[i].w) 36 { 37 dis[edge[i].v]=dis[edge[i].u]+edge[i].w; 38 if(!vis[edge[i].v]) vis[edge[i].v]=1,q.push(edge[i].v); 39 } 40 } 41 } 42 int main()/*S到其他节点的最短路*/ 43 { 44 memset(head,-1,sizeof(head)); 45 read(N);read(M);read(S); 46 for(int i=1;i<=N;i++) dis[i]=2147483647; dis[S]=0; 47 for(int i=1;i<=M;i++) 48 { 49 int x,y,z;read(x);read(y);read(z); 50 add_edge(x,y,z); 51 } 52 SPFA(); 53 for(int i=1;i<=N;i++) printf("%d ",dis[i]); 54 return 0; 55 }

1 #include<cstdio> 2 #include<deque> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=1000001; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 13 struct node 14 { 15 int u,v,w,nxt; 16 }edge[MAXN]; 17 int head[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y,int z) 20 { 21 edge[num].u=x; edge[num].v=y; 22 edge[num].w=z; edge[num].nxt=head[x]; 23 head[x]=num++; 24 } 25 int N,M,S=1;; 26 int dis[MAXN],vis[MAXN]; 27 inline void SPFA() 28 { 29 deque<int>q;q.push_front(S); 30 while(q.size()!=0) 31 { 32 int p=q.front(); 33 q.pop_front();vis[p]=0; 34 for(int i=head[p];i!=-1;i=edge[i].nxt) 35 if(dis[edge[i].v]>dis[edge[i].u]+edge[i].w) 36 { 37 dis[edge[i].v]=dis[edge[i].u]+edge[i].w; 38 if(!vis[edge[i].v]) vis[edge[i].v]=1,q.size()!=0&&dis[edge[i].v]<dis[q.front()]?q.push_front(edge[i].v):q.push_back(edge[i].v); 39 } 40 } 41 } 42 int main()/*S到其他节点的最短路*/ 43 { 44 memset(head,-1,sizeof(head)); 45 read(N);read(M);read(S); 46 for(int i=1;i<=N;i++) dis[i]=2147483647; dis[S]=0; 47 for(int i=1;i<=M;i++) 48 { 49 int x,y,z;read(x);read(y);read(z); 50 add_edge(x,y,z); 51 } 52 SPFA(); 53 for(int i=1;i<=N;i++) printf("%d ",dis[i]); 54 return 0; 55 }

1 #include<cstdio> 2 #include<cstring> 3 #include<ext/pb_ds/priority_queue.hpp> 4 using namespace __gnu_pbds; 5 const int MAXN=1000001; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 13 struct node 14 { 15 int u,v,w,nxt; 16 }edge[MAXN]; 17 int head[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y,int z) 20 { 21 edge[num].u=x; edge[num].v=y; 22 edge[num].w=z; edge[num].nxt=head[x]; 23 head[x]=num++; 24 } 25 int N,M,S=1;; 26 int dis[MAXN],vis[MAXN]; 27 struct Compare 28 { 29 __inline__ __attribute((always_inline)) bool operator()(int a,int b)//我以前的题解提到过的强制inline的方法 30 { 31 return dis[a]>dis[b]; 32 } 33 };//自定义比较器 34 inline void SPFA() 35 { 36 priority_queue<int,Compare>q; 37 q.push(S); 38 while(q.size()!=0) 39 { 40 int p=q.top(); 41 q.pop();vis[p]=0; 42 for(int i=head[p];i!=-1;i=edge[i].nxt) 43 if(dis[edge[i].v]>dis[edge[i].u]+edge[i].w) 44 { 45 dis[edge[i].v]=dis[edge[i].u]+edge[i].w; 46 if(!vis[edge[i].v]) vis[edge[i].v]=1,q.push(edge[i].v); 47 } 48 } 49 } 50 int main()/*S到其他节点的最短路*/ 51 { 52 memset(head,-1,sizeof(head)); 53 read(N);read(M);read(S); 54 for(int i=1;i<=N;i++) dis[i]=2147483647; dis[S]=0; 55 for(int i=1;i<=M;i++) 56 { 57 int x,y,z;read(x);read(y);read(z); 58 add_edge(x,y,z); 59 } 60 SPFA(); 61 for(int i=1;i<=N;i++) printf("%d ",dis[i]); 62 return 0; 63 }
Floyd

1 #include<cstdio> 2 #include<queue> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=2501; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 long long int map[MAXN][MAXN]; 13 int main()/*S到T的最短路*/ 14 { 15 int N,M,S,T; 16 read(N);read(M);read(S);read(T); 17 for(int i=1;i<=N;i++) for(int j=1;j<=N;j++) map[i][j]=0x7fffff; 18 for(int i=1;i<=M;i++) 19 { 20 int x,y,z;read(x);read(y);read(z); 21 map[x][y]=z;map[y][x]=z; 22 } 23 for(int k=1;k<=N;k++) 24 for(int i=1;i<=N;i++) 25 for(int j=1;j<=N;j++) 26 map[i][j]=min(map[i][j],map[i][k]+map[k][j]); 27 printf("%lld ",map[S][T]); 28 return 0; 29 }

1 #include<cstdio> 2 #include<queue> 3 #include<cstring> 4 using namespace std; 5 const int MAXN=2501; 6 inline void read(int &n) 7 { 8 char c=getchar();bool flag=0;n=0; 9 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 10 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 11 } 12 long long int map[MAXN][MAXN]; 13 int main()/*S到T的最短路*/ 14 { 15 int N,M,S,T; 16 read(N);read(M);read(S);read(T); 17 for(int i=1;i<=N;i++) for(int j=1;j<=N;j++) map[i][j]=0x7fffff; 18 for(int i=1;i<=M;i++) 19 { 20 int x,y,z;read(x);read(y);read(z); 21 map[x][y]=z;map[y][x]=z; 22 } 23 for(int k=1;k<=N;k++) 24 for(int i=1;i<=N;i++) 25 for(int j=1;j<=i;j++) 26 map[j][i]=map[i][j]=min(map[i][j],map[i][k]+map[k][j]); 27 printf("%lld ",map[S][T]); 28 return 0; 29 }
堆优化dijkstra

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<algorithm> #include<cstring> #include<ext/pb_ds/priority_queue.hpp> #define MP(x, y) make_pair(x, y) #define Pair pair<int, int> using namespace std; const int MAXN = 1e6 + 10, INF = 2147483646, B = 19; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = 1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M, S; struct Edge { int u, v, w, nxt; }E[MAXN]; int head[MAXN], num = 1; void AddEdge(int x, int y, int z) { E[num] = (Edge) {x, y, z, head[x]}; head[x] = num++; } int dis[MAXN], vis[MAXN]; priority_queue<Pair> q; void Dij() { for(int i = 1; i <= N; i++) dis[i] = 2147483647; dis[S] = 0; q.push(MP(0, S)); while(!q.empty()) { int p = q.top().second; q.pop(); if(vis[p]) continue; vis[p] = 1; for(int i = head[p]; i != -1; i = E[i].nxt) { int to = E[i].v; if(dis[to] > dis[p] + E[i].w) dis[to] = dis[p] + E[i].w, q.push(MP(-dis[to], to)); } } for(int i = 1; i <= N; i++) printf("%d ", dis[i]); } main() { memset(head, -1, sizeof(head)); N = read(); M = read(); S = read(); for(int i = 1; i <= M; i++) { int x = read(), y = read(), z = read(); AddEdge(x, y, z); } Dij(); return 0; }
最小生成树
Kruskal

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 using namespace std; 7 const int MAXN=400002; 8 inline void read(int &n) 9 { 10 char c=getchar();bool flag=0;n=0; 11 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 12 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 13 } 14 struct node 15 { 16 int u,v,w; 17 }edge[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y,int z) 20 { 21 edge[num].u=x; 22 edge[num].v=y; 23 edge[num].w=z; 24 num++; 25 } 26 int comp(const node &a,const node &b) 27 { 28 return a.w<b.w; 29 } 30 int fa[MAXN]; 31 int n,m; 32 int find(int x) 33 { 34 if(fa[x]==x) return fa[x]; 35 else return fa[x]=find(fa[x]); 36 } 37 int unionn(int x,int y) 38 { 39 fa[find(x)]=find(y); 40 } 41 inline void Kruskal() 42 { 43 int ans=0,tot=0; 44 sort(edge+1,edge+num,comp); 45 for(int i=1;i<=num-1;i++) 46 { 47 if(find(edge[i].u)!=find(edge[i].v)) 48 { 49 unionn(edge[i].u,edge[i].v); 50 tot++; 51 ans+=edge[i].w; 52 if(tot==n-1) 53 { 54 printf("%d",ans); 55 exit(0); 56 } 57 } 58 } 59 printf("orz"); 60 } 61 int main() 62 { 63 read(n);read(m); 64 for(int i=1;i<=n;i++) fa[i]=i; 65 for(int i=1;i<=m;i++) 66 { 67 int x,y,z; 68 read(x);read(y);read(z); 69 add_edge(x,y,z); 70 } 71 Kruskal(); 72 return 0; 73 }
tarjan

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<stack> #include<vector> #include<queue> #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) char buf[1<<21],*p1=buf,*p2=buf; using namespace std; const int MAXN=1000001; const int INF=1e9+7; inline int read() { char c=getchar();register int x=0; while(c<'0'||c>'9')c=getchar(); while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar(); return x; } char obuf[1<<24],*O=obuf; inline void print(int x) { if(x>9) print(x/10); *O++=x%10+'0'; } int val[MAXN]; struct node { int u,v,nxt; }edge[MAXN]; int head[MAXN],num=1; inline void AddEdge(int x,int y) { edge[num].u=x; edge[num].v=y; edge[num].nxt=head[x]; head[x]=num++; } vector<int>E[MAXN]; int color[MAXN],colornum=0,low[MAXN],dfn[MAXN],vis[MAXN],sum[MAXN],tot=0; stack<int>s; void tarjan(int now) { dfn[now]=low[now]=++tot; s.push(now);vis[now]=1; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]) tarjan(edge[i].v),low[now]=min(low[now],dfn[edge[i].v]); if(vis[edge[i].v]) low[now]=min(low[now],low[edge[i].v]); } if(low[now]==dfn[now]) { int h;colornum++; do { h=s.top(); color[h]=colornum; sum[colornum]+=val[h]; vis[h]=0; s.pop(); }while(now!=h); } } int inder[MAXN],dp[MAXN],ans=0; void Topsort() { queue<int>q; for(int i=1;i<=colornum;i++) dp[i]=sum[i]; for(int i=1;i<=colornum;i++) if(inder[i]==0) q.push(i); while(q.size()!=0) { int p=q.front();q.pop(); for(int i=0;i<E[p].size();i++) { inder[E[p][i]]--; dp[E[p][i]]=max(dp[E[p][i]],dp[p]+sum[E[p][i]]); if(inder[E[p][i]]==0) q.push(E[p][i]); } } for(int i=1;i<=colornum;i++) ans=max(ans,dp[i]); printf("%d",ans); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif memset(head,-1,sizeof(head)); int N=read(),M=read(); for(int i=1;i<=N;i++) val[i]=read(); for(int i=1;i<=M;i++) { int x=read(),y=read(); AddEdge(x,y); } for(int i=1;i<=N;i++) if(!color[i]) tarjan(i); for(int i=1;i<=N;i++) for(int j=head[i];j!=-1;j=edge[j].nxt) if(color[i]!=color[edge[j].v]) E[color[i]].push_back(color[edge[j].v]), inder[color[edge[j].v]]++; Topsort(); return 0; }

void tarjan(int now) { dfn[now]=low[now]=++tot; s.push(now); vis[now]=1; for(int i=headE[now];i!=-1;i=E[i].nxt) { if(!dfn[E[i].v]) tarjan(E[i].v),low[now]=min(low[now],low[E[i].v]); else if(vis[E[i].v]) low[now]=min(low[now],dfn[E[i].v]); } if(low[now]==dfn[now]) { int h; colornum++; do { h=s.top(); color[h]=colornum; sum[colornum]+=money[h]; vis[h]=0; s.pop(); }while(h!=now); } }

void tarjan(int now,int fa) { dfn[now]=low[now]=++tot; s.push(now); for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]&&edge[i].v!=fa) { tarjan(edge[i].v,now); low[now]=min(low[now],low[edge[i].v]); if(low[edge[i].v]>=dfn[now]) { memset(in,0,sizeof(in));//哪些在双联通分量里 memset(color,0,sizeof(color)); int h=0,cnt=0; do { h=s.top();s.pop(); in[h]=1; point[++cnt]=h; }while(h!=edge[i].v);//warning if(cnt<=1) continue;//必须构成环 in[now]=1;point[++cnt]=now; if(MakeColor(now,1)==0) for(int j=1;j<=cnt;j++) ans[point[j]]=1; } } if(edge[i].v!=fa) low[now]=min(low[now],dfn[edge[i].v]); } }

void tarjan(int now,int fa) { dfn[now]=low[now]=++tot; s.push(now); vis[now]=1; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]&&edge[i].v!=fa) tarjan(edge[i].v,now),low[now]=min(low[now],low[edge[i].v]); if(vis[edge[i].v]&&edge[i].v!=fa) low[now]=min(low[now],dfn[edge[i].v]); } if(dfn[now]==low[now]) { int h=0; colornum++; do { h=s.top(); color[h]=colornum; s.pop(); }while(h!=now); } }

int tarjan(int now,int fa) { int ch=0; dfn[now]=low[now]=++tot; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]) { tarjan(edge[i].v,fa); low[now]=min(low[now],low[edge[i].v]); if(low[edge[i].v]>=dfn[now]&&now!=fa) cut[now]=1; if(now==fa) ch++; } low[now]=min(low[now],dfn[edge[i].v]); } if(now==fa&&ch>=2) cut[now]=1; }

void tarjan(int now,int fa) { dfn[now]=low[now]=++tot; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(!dfn[edge[i].v]) { deep[edge[i].v]=deep[now]+1; f[edge[i].v]=now; tarjan(edge[i].v,now); low[now]=min(low[now],low[edge[i].v]); if(low[edge[i].v]>dfn[now]) { bridge[edge[i].v]=1; ans++; } } else if(edge[i].v!=fa) low[now]=min(low[now],dfn[edge[i].v]); } }
数论
BSGS

int BSGS(int a, int b, int p) {//a^x = b % p int M = ceil(sqrt(p)), base = fp(a, M), g = __gcd(a, p); if(g != 1) return -1; static map<int, int> mp; mp.clear(); for(int i = 0, now = b; i <= M; i++, now = mul(now, a)) mp[now] = i + 1; for(int i = 1, now = base; i <= M; i++, now = mul(now, base)) if(mp[now]) return i * M - mp[now] + 1; return -1; }
扩展欧几里得
https://www.luogu.org/problem/show?pid=1082

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 const int MAXN=100001; 9 inline void read(int &n) 10 { 11 char c=getchar();bool flag=0;n=0; 12 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 13 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 14 } 15 int a[6],b[6]; 16 int exgcd(int a,int b,int &x,int &y) 17 { 18 if(b==0) 19 { x=1,y=0;return a; } 20 int r=exgcd(b,a%b,x,y); 21 int tmp=x;x=y;y=tmp-(a/b)*y; 22 return r; 23 } 24 int x,y; 25 int main() 26 { 27 int a,b; 28 read(a);read(b); 29 int r=exgcd(a,b,x,y); 30 while(x<0) x+=b; 31 printf("%d",x); 32 return 0; 33 }

int x, y; int exgcd(int a, int b, int &x, int &y) { if(b == 0) {x = 1, y = 0; return a;} int r = exgcd(b, a % b, x, y), tmp; tmp = x; x = y; y = tmp - a / b * y; return r; } int solve(int a, int b, int mod) {//ax + mody = b int g = exgcd(a, mod, x, y); if(b % g) return -1; x = mul(x, (b / g)); mod = mod / g; while(x < 0) x += mod; return x % mod; }
CRT

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 #define LL long long 8 using namespace std; 9 const LL MAXN=100001; 10 const LL n=4; 11 inline void read(LL &n) 12 { 13 char c=getchar();bool flag=0;n=0; 14 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 15 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 16 } 17 LL a[MAXN],b[MAXN]; 18 LL exgcd(LL a,LL b,LL &x,LL &y) 19 { 20 if(b==0) 21 { x=1,y=0;return a; } 22 LL r=exgcd(b,a%b,x,y); 23 LL tmp=x;x=y;y=tmp-(a/b)*y; 24 return r; 25 } 26 LL x,y; 27 LL gcd(LL a,LL b) 28 { 29 return b==0?a:gcd(b,a%b); 30 } 31 LL CRT() 32 { 33 LL M=1,ans=0; 34 for(LL i=1;i<=n;i++) M*=a[i]; 35 for(LL i=1;i<=n;i++) 36 { 37 LL r=exgcd(M/a[i],a[i],x,y); 38 ans=( ans+b[i]*(M/a[i])*x )%M; 39 } 40 while(ans<0) ans+=M; 41 return ans; 42 } 43 int main() 44 { 45 46 for(LL i=1;i<=n;i++) 47 read(a[i]),read(b[i]); 48 printf("%lld",CRT()); 49 return 0; 50 }
扩展CRT

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<algorithm> 6 #include<queue> 7 using namespace std; 8 const int MAXN=100001; 9 const int n=4; 10 inline void read(int &n) 11 { 12 char c=getchar();bool flag=0;n=0; 13 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 14 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 15 } 16 int a[MAXN],b[MAXN]; 17 int exgcd(int a,int b,int &x,int &y) 18 { 19 if(b==0) 20 { x=1,y=0;return a; } 21 int r=exgcd(b,a%b,x,y); 22 int tmp=x;x=y;y=tmp-(a/b)*y; 23 return r; 24 } 25 int x,y; 26 int gcd(int a,int b) 27 { 28 return b==0?a:gcd(b,a%b); 29 } 30 inline int EX_CRT() 31 { 32 /* 33 x+a1*y1=b1 1 34 x+a2*y2=b2 2 35 x+a3*y3=b3 3 36 求这个方程的解x 37 */ 38 int M=a[1],R=b[1],x,y; 39 // M=LCM(a1,a2) 40 // R=bi-b1 41 for(int i=2;i<=n;i++) 42 { 43 44 /* 45 a1*y1-a2*y2=b2-b1 46 a*x +b*y =gcd(a,b) 47 这样求出y1之后 48 带回得到对于1,2两个方程的解x0=b1-y1*a1 49 */ 50 int r=exgcd(M,a[i],x,y); 51 if( (R-b[i])%r!=0) return -1; 52 /* R-b[i]相当于b2-b1 53 方程有解的条件(b2-b1)%gcd(a,b) ==0 */ 54 55 x=(R-b[i])/r*x%a[i];//**** 56 57 58 R=R-x*M;//x0=b1-y1*a1 59 M=M/r*a[i];// 新的模数 60 R=R%M;//R=X mod M 61 } 62 return (R%M+M)%M; 63 } 64 int main() 65 { 66 67 for(int i=1;i<=n;i++) 68 read(a[i]),read(b[i]); 69 printf("%d",EX_CRT()); 70 return 0; 71 }
快速幂

1 #include<cstdio> 2 #include<deque> 3 #include<cstring> 4 #define LL long long 5 using namespace std; 6 const LL MAXN=1000001; 7 inline void read(LL &n) 8 { 9 char c=getchar();bool flag=0;n=0; 10 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 11 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 12 } 13 LL a,p,mod,base; 14 LL fastpow(LL a,LL p) 15 { 16 for(base=1;p;p>>=1) p&1?base=(base*a)%mod,a=(a*a)%mod:a=(a*a)%mod; 17 return base; 18 } 19 int main() 20 { 21 22 read(a);read(p);read(mod); 23 printf("%lld^%lld mod %lld=%lld",a,p,mod,fastpow(a,p)); 24 return 0; 25 }
卡特兰数
https://www.luogu.org/problem/show?pid=1976

1 #include<cstdio> 2 const int MAXN=100001; 3 inline int read() 4 { 5 char c=getchar();int x=0,flag=1; 6 while(c<'0'||c>'9') {if(c=='-') flag=-1;c=getchar();} 7 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*flag; 8 } 9 int n; 10 long long dp[MAXN]; 11 int main() 12 { 13 n=read(); 14 dp[0]=1; 15 int ans=0; 16 for(int i=1;i<=n;i++) 17 for(int j=0;j<i;j++) 18 dp[i]=(dp[i]+(dp[j]*dp[i-j-1])%100000007)%100000007; 19 printf("%lld",dp[n]%100000007); 20 return 0; 21 }
字符串
KMP

#include<cstdio> #include<cstring> using namespace std; const int MAXN = 1e6 + 10; char s1[MAXN], s2[MAXN]; int N1, N2; int fail[MAXN]; void GetFail() { int now = 0; for(int i = 2; i <= N2; i++) { while(now && s2[i] != s2[now + 1]) now = fail[now]; if(s2[i] == s2[now + 1]) now++; fail[i] = now; } } void KMP() { int now = 0; for(int i = 1; i <= N1; i++) { while(now && s1[i] != s2[now + 1]) now = fail[now]; if(s1[i] == s2[now + 1]) now++; if(now == N2) printf("%d ", i - N2 + 1), now= fail[now]; } } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); //freopen("a.out", "w", stdout); #endif scanf("%s %s", s1 + 1, s2 + 1); N1 = strlen(s1 + 1); N2 = strlen(s2 + 1); GetFail(); KMP(); for(int i = 1; i <= N2; i++) printf("%d ", fail[i]); return 0; }
后缀数组
http://www.cnblogs.com/zwfymqz/p/8430014.html

#include<cstdio> #include<iostream> #include<cstring> using namespace std; const int MAXN=2*1e6+10; int sa[MAXN],rak[MAXN],tp[MAXN],tax[MAXN],a[MAXN],N,M,height[MAXN]; char s[MAXN]; void Qsort() { for(int i=1;i<=M;i++) tax[i]=0; for(int i=1;i<=N;i++) tax[rak[i]]++; for(int i=1;i<=M;i++) tax[i]+=tax[i-1]; for(int i=N;i>=1;i--) sa[ tax[rak[tp[i]]]-- ] = tp[i]; } void Ssort() { M=127; for(int i=1;i<=N;i++) rak[i]=a[i],tp[i]=i;Qsort(); for(int w=1,p=1; p<N ; w<<=1,M=p) { p=0; for(int i=N-w+1;i<=N;i++) tp[++p]=i; for(int i=1;i<=N;i++) if(sa[i]>w) tp[++p]=sa[i]-w; Qsort(); swap(tp,rak); rak[sa[1]]=1;p=1; for(int i=2;i<=N;i++) rak[sa[i]] = (tp[sa[i]]==tp[sa[i-1]]&&tp[sa[i]+w]==tp[sa[i-1]+w])?p:++p; } int j,k=0; for(int i=1;i<=N;height[rak[i++]]=k) for(k=k?k-1:k,j=sa[rak[i]-1];a[i+k]==a[j+k];++k ); for(int i=0;i<=N;i++) { for(int j=height[i]+1;;j++) { int tot=1; for(int k=i+1;height[k]>=j;++k,++tot); if(tot>1) printf("%d ",tot); else break; } } } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif int Meiyong; cin>>Meiyong; scanf("%s",s); N=strlen(s); for(int i=1;i<=N;i++) a[i]=s[i-1]; Ssort(); return 0; }
后缀自动机

// luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<vector> #define LL long long using namespace std; const int MAXN = 2 * 1e6 + 10; char s[MAXN]; int N; int last = 1, root = 1, tot = 1, fa[MAXN], ch[MAXN][26], len[MAXN], siz[MAXN]; void insert(int x) { int now = ++tot, pre = last; last = now; //last代表全串的点,这里不能简单的写tot - 1,因为当第三种情况时候会增加新的节点 len[now] = len[pre] + 1; siz[now] = 1; //在新加入节点后,最长的后缀的right集合大小肯定为1 for(; pre && !ch[pre][x]; pre = fa[pre]) ch[pre][x] = now; if(!pre) fa[now] = root; else { int q = ch[pre][x];//q是pre的祖先 pre -> q //说明pre有一条x转移边 q = pre + x if(len[q] == len[pre] + 1) fa[now] = q; else {//right集合不完全重合 int nows = ++tot; len[nows] = len[pre] + 1; //这里的nows用于接收len[q] <= len[pre] + 1的点 //q用于接收len[q] > len[pre] + 1 的点 memcpy(ch[nows], ch[q], sizeof(ch[q])); //这里ch[q]能转移到的,ch[nows]也一定能转移到,因为ch[nows]表示ch[q]去掉前几个字符后的串 fa[nows] = fa[q]; fa[q] = fa[now] = nows; //以前的fa[q]满足max[fa[q]] = min[q] + 1,而nows表示的串长度一定包含q里面最小的,因此fa[nows]的爸爸就是fa[q] //此时的nows表示的节点一定是q,now表示的节点的后缀, for(; pre && ch[pre][x] == q; pre = fa[pre]) ch[pre][x] = nows; //此时的pre保证可以走到q,那么pre的祖先一定是pre的后缀,他们的长度一定都是小于等于nows的 } } } vector<int> v[MAXN]; LL ans = 0; void dfs(int x) { for(int i = 0; i < v[x].size(); i++) { int to = v[x][i]; dfs(to), siz[x] += siz[to]; } //是否存在父亲出现了但是儿子没出现的情况? if(siz[x] > 1) ans = max(ans, 1ll * siz[x] * len[x]); } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif scanf("%s", s + 1); N = strlen(s + 1); for(int i = 1; i <= N; i++) insert(s[i] - 'a'); for(int i = 2; i <= tot; i++) v[fa[i]].push_back(i); dfs(root); printf("%lld", ans); return 0; }
AC自动机

// luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<queue> #include<vector> using namespace std; const int MAXN = 1e6 + 10, B = 26; int T; char s[201][75], a[MAXN]; int N; int fail[MAXN], ch[MAXN][27], val[MAXN], root = 0, tot = 0, sum[MAXN]; void insert(char *s, int I) { int N = strlen(s + 1); int now = root; for(int i = 1; i <= N; i++) { int x = s[i] - 'a'; if(!ch[now][x]) ch[now][x] = ++tot; now = ch[now][x]; } val[now] = I; } void GetFail() { queue<int> q; for(int i = 0; i < B; i++) if(ch[root][i]) q.push(ch[root][i]); while(!q.empty()) { int p = q.front(); q.pop(); for(int i = 0; i < B; i++) if(ch[p][i]) fail[ch[p][i]] = ch[fail[p]][i], q.push(ch[p][i]); else ch[p][i] = ch[fail[p]][i]; } } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif while(scanf("%d", &T) && T) { memset(fail, 0, sizeof(fail)); memset(ch, 0, sizeof(ch)); memset(val, 0, sizeof(val)); memset(fail, 0, sizeof(fail)); memset(sum, 0, sizeof(sum)); memset(s, 0, sizeof(s)); for(int i = 1; i <= T; i++) scanf("%s", s[i] + 1), insert(s[i], i); GetFail(); scanf("%s", a + 1); int N = strlen(a + 1), now = root; for(int i = 1; i <= N; i++) { now = ch[now][a[i] - 'a']; for(int t = now; t; t = fail[t]) if(val[t]) sum[val[t]]++; } int ans = 0; for(int i = 1; i <= T; i++) ans = max(ans, sum[i]); printf("%d ", ans); for(int i = 1; i <= T; i++) if(sum[i] == ans) printf("%s ", s[i] + 1); } return 0; }
数据结构
堆

1 struct S 2 { 3 int pos,val; 4 S(){ pos=0;val=0; } 5 S(int a,int b){ pos=a,val=b; } 6 7 }; 8 bool operator <(const S &a,const S &b) 9 { 10 return a.pos>b.pos; 11 }//按照位置从小到大排序 12 priority_queue<S>q;
单调队列
https://www.luogu.org/problem/show?pid=1886

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<deque> 6 using namespace std; 7 const int MAXN=1000010; 8 inline void read(int &n) 9 { 10 char c=getchar();n=0;bool flag=0; 11 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 12 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 13 } 14 struct node 15 { 16 int pos,val; 17 node(){pos=val=0;} 18 node(int a,int b) { pos=a;val=b; } 19 }; 20 deque<node>q; 21 int a[MAXN]; 22 int main() 23 { 24 int n,k; 25 read(n);read(k); 26 for(int i=1;i<=n;i++) read(a[i]); 27 for(int i=1;i<=n;i++) 28 { 29 while(q.size()>0&&q.front().pos<=(i-k)) q.pop_front(); 30 while(q.size()>0&&a[i]<q.back().val) q.pop_back(); 31 q.push_back(node(i,a[i])); 32 if(i>=k) printf("%d ",q.front().val); 33 } 34 printf(" "); 35 while(q.size()!=0) q.pop_front(); 36 for(int i=1;i<=n;i++) 37 { 38 while(q.size()>0&&q.front().pos<=(i-k)) q.pop_front(); 39 while(q.size()>0&&a[i]>q.back().val) q.pop_back(); 40 q.push_back(node(i,a[i])); 41 if(i>=k) printf("%d ",q.front().val); 42 } 43 return 0; 44 }
线段树
单点修改&&区间求和http://codevs.cn/problem/1080/

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define ls k<<1 6 #define rs k<<1|1 7 using namespace std; 8 const int MAXN=400400; 9 inline void read(int &n) 10 { 11 char c=getchar();n=0;bool flag=0; 12 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 13 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 14 } 15 struct node 16 { 17 int l,r,w,f; 18 }tree[MAXN]; 19 int ans=0; 20 inline void update(int k) 21 { tree[k].w=tree[ls].w+tree[rs].w; } 22 inline void Build_Tree(int ll,int rr,int k) 23 { 24 tree[k].l=ll;tree[k].r=rr; 25 if(ll==rr) 26 { read(tree[k].w); return ; } 27 int mid=tree[k].l+tree[k].r>>1; 28 Build_Tree(ll,mid,ls); Build_Tree(mid+1,rr,rs); 29 update(k); 30 } 31 void Point_Add(int k,int pos,int val) 32 { 33 if(tree[k].l==tree[k].r) 34 { tree[k].w+=val; return ; } 35 int mid= tree[k].l+tree[k].r>>1; 36 if(pos<=mid) Point_Add(ls,pos,val); 37 else Point_Add(rs,pos,val); 38 update(k); 39 } 40 void Interval_Sum(int k,int ll,int rr) 41 { 42 if(ll<=tree[k].l&&tree[k].r<=rr) 43 { ans+=tree[k].w; return ; } 44 int mid=tree[k].l+tree[k].r>>1; 45 if(ll<=mid) Interval_Sum(ls,ll,rr); 46 if(rr>mid) Interval_Sum(rs,ll,rr); 47 } 48 int main() 49 { 50 int n,m; 51 read(n); 52 Build_Tree(1,n,1); 53 read(m); 54 for(int i=1;i<=m;i++) 55 { 56 int how;read(how); 57 if(how==1) 58 { 59 int pos,val; read(pos);read(val); 60 Point_Add(1,pos,val); 61 } 62 else 63 { 64 int a,b;read(a);read(b); ans=0; 65 Interval_Sum(1,a,b); 66 printf("%d ",ans); 67 } 68 } 69 return 0; 70 }
区间修改&&区间求和http://codevs.cn/problem/1082/

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define ls k<<1 6 #define rs k<<1|1 7 #define LL long long 8 using namespace std; 9 const LL MAXN=800400; 10 inline void read(LL &n) 11 { 12 char c=getchar();n=0;bool flag=0; 13 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 14 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 15 } 16 struct node 17 { 18 LL l,r,w,f; 19 }tree[MAXN]; 20 LL ans=0; 21 inline void update(LL k) 22 { tree[k].w=tree[ls].w+tree[rs].w; } 23 inline void Build_Tree(LL ll,LL rr,LL k) 24 { 25 tree[k].l=ll;tree[k].r=rr; 26 if(ll==rr) 27 { read(tree[k].w); return ; } 28 LL mid=tree[k].l+tree[k].r>>1; 29 Build_Tree(ll,mid,ls); Build_Tree(mid+1,rr,rs); 30 update(k); 31 } 32 inline void down(LL k) 33 { 34 tree[ls].w+=(tree[ls].r-tree[ls].l+1)*tree[k].f; 35 tree[rs].w+=(tree[rs].r-tree[rs].l+1)*tree[k].f; 36 tree[ls].f+=tree[k].f; 37 tree[rs].f+=tree[k].f; 38 tree[k].f=0; 39 } 40 inline void Interval_Add(LL k,LL ll,LL rr,LL val) 41 { 42 if(ll<=tree[k].l&&tree[k].r<=rr) 43 { 44 tree[k].w+=(tree[k].r-tree[k].l+1)*val; 45 tree[k].f+=val; 46 return ; 47 } 48 if(tree[k].f) down(k); 49 LL mid=tree[k].l+tree[k].r>>1; 50 if(ll<=mid) Interval_Add(ls,ll,rr,val); 51 if(rr>mid) Interval_Add(rs,ll,rr,val); 52 update(k); 53 } 54 inline void Interval_Sum(LL k,LL ll,LL rr) 55 { 56 if(ll<=tree[k].l&&tree[k].r<=rr) 57 { 58 ans+=tree[k].w; 59 return ; 60 } 61 if(tree[k].f) down(k); 62 LL mid=tree[k].l+tree[k].r>>1; 63 if(ll<=mid) Interval_Sum(ls,ll,rr); 64 if(rr>mid) Interval_Sum(rs,ll,rr); 65 } 66 int main() 67 { 68 LL n,m; 69 read(n); 70 Build_Tree(1,n,1); 71 read(m); 72 for(LL i=1;i<=m;i++) 73 { 74 LL how;read(how); 75 if(how==1) 76 { 77 LL x,y,val;read(x);read(y);read(val); 78 Interval_Add(1,x,y,val); 79 } 80 else 81 { 82 LL x,y;read(x);read(y); 83 ans=0; 84 Interval_Sum(1,x,y); 85 printf("%lld ",ans); 86 } 87 } 88 return 0; 89 }
区间修改&&单点修改http://codevs.cn/problem/1081/

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define ls k<<1 6 #define rs k<<1|1 7 using namespace std; 8 const int MAXN=400400; 9 inline void read(int &n) 10 { 11 char c=getchar();n=0;bool flag=0; 12 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 13 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 14 } 15 struct node 16 { 17 int l,r,w,f; 18 }tree[MAXN]; 19 int ans=0; 20 inline void update(int k) 21 { tree[k].w=tree[ls].w+tree[rs].w; } 22 inline void Build_Tree(int ll,int rr,int k) 23 { 24 tree[k].l=ll;tree[k].r=rr; 25 if(ll==rr) 26 { read(tree[k].w); return ; } 27 int mid=tree[k].l+tree[k].r>>1; 28 Build_Tree(ll,mid,ls); Build_Tree(mid+1,rr,rs); 29 update(k); 30 } 31 inline void down(int k) 32 { 33 tree[ls].w+=(tree[ls].r-tree[ls].l+1)*tree[k].f; 34 tree[rs].w+=(tree[rs].r-tree[rs].l+1)*tree[k].f; 35 tree[ls].f+=tree[k].f; 36 tree[rs].f+=tree[k].f; 37 tree[k].f=0; 38 update(k); 39 return ; 40 } 41 void Interval_Add(int k,int ll,int rr,int val) 42 { 43 if(ll<=tree[k].l&&tree[k].r<=rr) 44 { 45 tree[k].w=tree[k].w+(tree[k].r-tree[k].l+1)*val; 46 tree[k].f+=val; 47 return ; 48 } 49 if(tree[k].f) down(k); 50 int mid=tree[k].l+tree[k].r>>1; 51 if(ll<=mid) Interval_Add(ls,ll,rr,val); 52 if(rr>mid) Interval_Add(rs,ll,rr,val); 53 update(k); 54 } 55 void Point_Ask(int k,int pos) 56 { 57 if(tree[k].l==tree[k].r) 58 { 59 ans=tree[k].w; 60 return ; 61 } 62 if(tree[k].f) down(k); 63 int mid=tree[k].l+tree[k].r>>1; 64 if(pos<=mid) Point_Ask(ls,pos); 65 else Point_Ask(rs,pos); 66 } 67 int main() 68 { 69 int n,m; 70 read(n); 71 Build_Tree(1,n,1); 72 read(m); 73 for(int i=1;i<=m;i++) 74 { 75 int how;read(how); 76 if(how==1) 77 { 78 int x,y,val;read(x);read(y);read(val); 79 Interval_Add(1,x,y,val); 80 } 81 else 82 { 83 int pos;read(pos); 84 ans=0; 85 Point_Ask(1,pos); 86 printf("%d ",ans); 87 } 88 } 89 return 0; 90 }
区间修改&&区间覆盖&&区间求和&&最大值&&&最小值http://codevs.cn/problem/4927/

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define LL long long 6 #define ls k<<1 7 #define rs k<<1|1 8 using namespace std; 9 const LL MAXN=400400; 10 const LL INF =0x7fffff; 11 inline void read(LL &n) 12 { 13 char c=getchar();n=0;bool flag=0; 14 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 15 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 16 } 17 struct node 18 { 19 LL l,r,w,Max,Min,Set,Add; 20 bool V; 21 }tree[MAXN]; 22 LL n,m; 23 LL ans=0; 24 inline void update(LL k) 25 { 26 tree[k].w=tree[ls].w+tree[rs].w; 27 tree[k].Max=max(tree[ls].Max,tree[rs].Max); 28 tree[k].Min=min(tree[ls].Min,tree[rs].Min); 29 } 30 void Build_Tree(LL ll,LL rr,LL k) 31 { 32 tree[k].l=ll;tree[k].r=rr; 33 if(tree[k].l==tree[k].r) 34 { 35 read(tree[k].w); 36 tree[k].Max=tree[k].w; 37 tree[k].Min=tree[k].w; 38 return ; 39 } 40 LL mid=tree[k].l+tree[k].r>>1; 41 Build_Tree(ll,mid,ls); 42 Build_Tree(mid+1,rr,rs); 43 update(k); 44 } 45 void down(LL k) 46 { 47 if(tree[k].V) 48 { 49 tree[ls].Add=0; 50 tree[ls].V=1; 51 tree[ls].w=(tree[ls].r-tree[ls].l+1)*tree[k].Set; 52 tree[ls].Max=tree[ls].Min=tree[ls].Set=tree[k].Set; 53 54 tree[rs].Add=0; 55 tree[rs].V=1; 56 tree[rs].w=(tree[rs].r-tree[rs].l+1)*tree[k].Set; 57 tree[rs].Max=tree[rs].Min=tree[rs].Set=tree[k].Set; 58 59 tree[k].Set=tree[k].V=0; 60 } 61 if(tree[k].Add) 62 { 63 tree[ls].w+=(tree[ls].r-tree[ls].l+1)*tree[k].Add; 64 tree[ls].Add+=tree[k].Add; 65 tree[ls].Max+=tree[k].Add; 66 tree[ls].Min+=tree[k].Add; 67 68 tree[rs].w+=(tree[rs].r-tree[rs].l+1)*tree[k].Add; 69 tree[rs].Add+=tree[k].Add; 70 tree[rs].Max+=tree[k].Add; 71 tree[rs].Min+=tree[k].Add; 72 tree[k].Add=0; 73 } 74 75 } 76 void Interval_Add(LL k,LL ll,LL rr,LL val) 77 { 78 if(ll<=tree[k].l&&tree[k].r<=rr) 79 { 80 tree[k].w+=(tree[k].r-tree[k].l+1)*val; 81 tree[k].Add+=val; 82 tree[k].Max+=val; 83 tree[k].Min+=val; 84 return ; 85 } 86 if(tree[k].Add||tree[k].V) down(k); 87 LL mid=tree[k].r+tree[k].l>>1; 88 if(ll<=mid) Interval_Add(ls,ll,rr,val); 89 if(rr>mid) Interval_Add(rs,ll,rr,val); 90 update(k); 91 } 92 void Interval_Change(LL k,LL ll,LL rr,LL val) 93 { 94 if(ll<=tree[k].l&&tree[k].r<=rr) 95 { 96 tree[k].Max=tree[k].Min=val; 97 tree[k].Set=val;tree[k].V=1; 98 tree[k].w=(tree[k].r-tree[k].l+1)*val; 99 tree[k].Add=0; 100 return ; 101 } 102 if(tree[k].Add||tree[k].V) down(k); 103 LL mid=tree[k].r+tree[k].l>>1; 104 if(ll<=mid) Interval_Change(ls,ll,rr,val); 105 if(rr>mid) Interval_Change(rs,ll,rr,val); 106 update(k); 107 } 108 void Interval_Sum(LL k,LL ll,LL rr) 109 { 110 if(ll<=tree[k].l&&tree[k].r<=rr) 111 { 112 ans+=tree[k].w; 113 return ; 114 } 115 if(tree[k].Add||tree[k].V) down(k); 116 LL mid=tree[k].r+tree[k].l>>1; 117 if(ll<=mid) Interval_Sum(ls,ll,rr); 118 if(rr>mid) Interval_Sum(rs,ll,rr); 119 } 120 void Interval_Max(LL k,LL ll,LL rr) 121 { 122 if(ll<=tree[k].l&&tree[k].r<=rr) 123 { 124 ans=max(ans,tree[k].Max); 125 return ; 126 } 127 if(tree[k].Add||tree[k].V) down(k); 128 LL mid=tree[k].r+tree[k].l>>1; 129 if(ll<=mid) Interval_Max(ls,ll,rr); 130 if(rr>mid) Interval_Max(rs,ll,rr); 131 } 132 void Interval_Min(LL k,LL ll,LL rr) 133 { 134 if(ll<=tree[k].l&&tree[k].r<=rr) 135 { 136 ans=min(ans,tree[k].Min); 137 return ; 138 } 139 if(tree[k].Add||tree[k].V) down(k); 140 LL mid=tree[k].r+tree[k].l>>1; 141 if(ll<=mid) Interval_Min(ls,ll,rr); 142 if(rr>mid) Interval_Min(rs,ll,rr); 143 } 144 int main() 145 { 146 read(n);read(m); 147 Build_Tree(1,n,1); 148 for(LL i=1;i<=m;i++) 149 { 150 char how[5]; 151 scanf("%s",how); 152 if(how[0]=='a')//区间加 153 { 154 LL x,y,val;read(x);read(y);read(val); 155 Interval_Add(1,x,y,val); 156 } 157 else if(how[0]=='s'&&how[1]=='e')//区间赋值 158 { 159 LL x,y,val;read(x);read(y);read(val); 160 Interval_Change(1,x,y,val); 161 } 162 else if(how[0]=='s'&&how[1]=='u')//区间求和 163 { 164 LL x,y;read(x);read(y);ans=0; 165 Interval_Sum(1,x,y); 166 printf("%lld ",ans); 167 } 168 else if(how[0]=='m'&&how[1]=='a')//区间最大值 169 { 170 LL x,y;read(x);read(y);ans=0; 171 Interval_Max(1,x,y); 172 printf("%lld ",ans); 173 } 174 else if(how[0]=='m'&&how[1]=='i')// 区间最小值 175 { 176 LL x,y;read(x);read(y);ans=INF; 177 Interval_Min(1,x,y); 178 printf("%lld ",ans); 179 } 180 } 181 return 0; 182 }
区间乘区间加区间修改

// luogu-judger-enable-o2 // luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<cmath> #include<algorithm> #define ls k<<1 #define rs k<<1|1 #define int long long using namespace std; const int MAXN=1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int N,M,mod; namespace SegmentTree { struct node { int mul,add,sum,l,r,siz; }T[MAXN]; void update(int k) { T[k].sum=(T[ls].sum%mod+T[rs].sum%mod)%mod; } void ps(int x,int f) { T[x].mul=(T[x].mul%mod*T[f].mul%mod)%mod; T[x].add=(T[x].add*T[f].mul)%mod; T[x].add=(T[x].add+T[f].add)%mod; T[x].sum=(T[x].sum%mod*T[f].mul%mod)%mod; T[x].sum=(T[x].sum+T[f].add%mod*T[x].siz)%mod; } void pushdown(int k) { if(T[k].add==0&&T[k].mul==1) return ; ps(ls,k); ps(rs,k); T[k].add=0; T[k].mul=1; } void Build(int k,int ll,int rr) { T[k].l=ll;T[k].r=rr;T[k].siz=rr-ll+1;T[k].mul=1; if(ll==rr) { T[k].sum=read()%mod; return ; } int mid=ll+rr>>1; Build(ls,ll,mid); Build(rs,mid+1,rr); update(k); } void IntervalMul(int k,int ll,int rr,int val) { if(ll<=T[k].l&&T[k].r<=rr) { T[k].sum=(T[k].sum*val)%mod; T[k].mul=(T[k].mul*val)%mod; T[k].add=(T[k].add*val)%mod; return ; } pushdown(k); int mid=T[k].l+T[k].r>>1; if(ll<=mid) IntervalMul(ls,ll,rr,val); if(rr>mid) IntervalMul(rs,ll,rr,val); update(k); } void IntervalAdd(int k,int ll,int rr,int val) { if(ll<=T[k].l&&T[k].r<=rr) { T[k].sum=(T[k].sum+T[k].siz*val)%mod; T[k].add=(T[k].add+val)%mod; return ; } pushdown(k); int mid=T[k].l+T[k].r>>1; if(ll<=mid) IntervalAdd(ls,ll,rr,val); if(rr>mid) IntervalAdd(rs,ll,rr,val); update(k); } int IntervalSum(int k,int ll,int rr) { int ans=0; if(ll<=T[k].l&&T[k].r<=rr) { ans=(ans+T[k].sum)%mod; return ans; } pushdown(k); int mid=T[k].l+T[k].r>>1; if(ll<=mid) ans=(ans+IntervalSum(ls,ll,rr))%mod; if(rr>mid) ans=(ans+IntervalSum(rs,ll,rr))%mod; return ans%mod; } } main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif N=read();M=read();mod=read(); SegmentTree::Build(1,1,N); while(M--) { int opt=read(); if(opt==1) { int l=read(),r=read(),val=read()%mod; SegmentTree::IntervalMul(1,l,r,val); } else if(opt==2) { int l=read(),r=read(),val=read()%mod; SegmentTree::IntervalAdd(1,l,r,val); } else if(opt==3) { int l=read(),r=read(); printf("%lld ", SegmentTree::IntervalSum(1,l,r)%mod); } } return 0; }
树状数组
单点修改&&区间查询https://www.luogu.org/problem/show?pid=3374

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define lb(x) (x&(-x)) 6 using namespace std; 7 const int MAXN=500001; 8 inline int read() 9 { 10 char c=getchar();int x=0;int f=1; 11 while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} 12 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*f; 13 } 14 int tree[MAXN]; 15 int n=read(),m=read(); 16 inline void Point_Add(int pos,int val) 17 { 18 while(pos<=n) tree[pos]+=val,pos+=lb(pos); 19 } 20 inline int Interval_Sum(int pos) 21 { 22 int ans=0; 23 while(pos) ans+=tree[pos], pos-=lb(pos); 24 return ans; 25 } 26 int main() 27 { 28 29 for(int i=1;i<=n;i++) 30 { 31 int p=read();Point_Add(i,p); 32 } 33 for(int i=1;i<=m;i++) 34 { 35 int how=read(),x=read(),y=read(); 36 if(how==1) Point_Add(x,y); 37 else printf("%d ",Interval_Sum(y)-Interval_Sum(x-1)); 38 } 39 return 0; 40 }
区间修改&&单点查询https://www.luogu.org/problem/show?pid=3368

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define lb(x) (x&(-x)) 6 using namespace std; 7 const int MAXN=500001; 8 inline int read() 9 { 10 char c=getchar();int x=0;int f=1; 11 while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} 12 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*f; 13 } 14 int tree[MAXN]; 15 int n=read(),m=read(); 16 inline void Point_Add(int pos,int val) 17 { 18 while(pos<=n) tree[pos]+=val,pos+=lb(pos); 19 } 20 inline int Interval_Sum(int pos) 21 { 22 int ans=0; 23 while(pos) ans+=tree[pos], pos-=lb(pos); 24 return ans; 25 } 26 int main() 27 { 28 int pre=0; 29 for(int i=1;i<=n;i++) 30 { 31 int p=read();Point_Add(i,p-pre); 32 pre=p; 33 } 34 for(int i=1;i<=m;i++) 35 { 36 int how=read(),x=read(),y,val; 37 if(how==1) y=read(),val=read(),Point_Add(x,val),Point_Add(y+1,-val); 38 else printf("%d ",Interval_Sum(x)); 39 } 40 return 0; 41 }
平衡树
splay

#include<cstdio> #include<algorithm> using namespace std; const int MAXN = 4 * 1e5 + 10, INF = 1e9; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int T; #define ls(x) ch[x][0] #define rs(x) ch[x][1] #define root ch[0][1] int ch[MAXN][2], fa[MAXN], rev[MAXN], siz[MAXN], val[MAXN], tot = 0; int ident(int x) { return ch[fa[x]][0] == x ? 0 : 1;} void connect(int x, int _fa, int how) { fa[x] = _fa; ch[fa[x]][how] = x;} void update(int x) { siz[x] = siz[ls(x)] + siz[rs(x)] + rev[x];} void rotate(int x) { int Y = fa[x], R = fa[Y]; int Yson = ident(x), Rson = ident(Y); int B = ch[x][Yson ^ 1]; connect(x, R, Rson); connect(Y, x, Yson ^ 1); connect(B, Y, Yson); update(Y); update(x); } void splay(int x, int to) { to = fa[to]; while(fa[x] != to) { int y = fa[x]; if(fa[y] == to) rotate(x); else if(ident(x) == ident(y)) rotate(y), rotate(x); else rotate(x), rotate(x); } } int NewNode(int _fa, int v) { fa[++tot]= _fa; siz[tot] = rev[tot] = 1; val[tot] = v; return tot; } void insert(int v) { if(root == 0) {root = NewNode(0, v); return ;} int now = root; while(now) { siz[now]++; if(val[now] == v) {rev[now]++; splay(now, root); return ;} int nxt = v > val[now]; if(!ch[now][nxt]) {ch[now][nxt] = NewNode(now, v); splay(now, root); return ;} now = ch[now][nxt]; } } int find(int v) { int now = root; while(now) { if(val[now] == v) {splay(now, root); return now;} int nxt = v > val[now]; now = ch[now][nxt]; } } void erase(int v) { int now = find(v); if(rev[now] > 1) {rev[now]--; siz[now]--; return ;} else if(!ls(now) && !rs(now)) {root = 0; return ;} else if(!ls(now)) {root = rs(now); fa[rs(now)] = 0;} else { int l = ls(now); while(rs(l)) l = rs(l); splay(l, ls(now)); //ch[l][1] = rs(now); fa[rs(now)] = l; connect(rs(now), l, 1); connect(l, 0, 1); update(l); } } int rak(int v) { int pos = find(v); return siz[ch[pos][0]] + 1; } int kth(int v) { int now = root; while(now) { int used = siz[now] - siz[rs(now)]; if(v <= used && v > siz[ls(now)]) return val[now]; if(v > used) now = ch[now][1], v -= used; else now = ch[now][0]; } } int pre(int v) { int ans = -INF, now = root; while(now) { if(val[now] < v) ans = max(ans, val[now]); int nxt = v <= val[now] ? 0 : 1; now = ch[now][nxt]; } return ans; } int nxt(int v) { int ans = INF, now = root; while(now) { if(val[now] > v) ans = min(ans, val[now]); int nxt = v < val[now] ? 0 : 1; now = ch[now][nxt]; } return ans; } int main() { T = read(); while(T--) { int opt = read(), x = read(); if(opt == 1) insert(x); else if(opt == 2) erase(x); else if(opt == 3) printf("%d ", rak(x)); else if(opt == 4) printf("%d ", kth(x)); else if(opt == 5) printf("%d ", pre(x)); else if(opt == 6) printf("%d ", nxt(x)); } return 0; }
Treap

#include<iostream> #include<cstdio> #include<cstdlib> #define ls tree[k].l #define rs tree[k].r using namespace std; const int MAXN=1e6+10; inline char nc() { static char buf[MAXN],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin))?EOF:*p1++; } inline int read() { char c=nc();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();} while(c>='0'&&c<='9'){x=x*10+c-'0',c=nc();} return x*f; } struct node { int l,r,tot,recy,val,rd; }tree[MAXN]; int size,root,ans=0; inline void update(int k) { tree[k].tot=tree[ls].tot+tree[rs].tot+tree[k].recy; } inline void insert(int &k,int x) { if(k==0) { ++size;k=size; tree[size].recy=tree[size].tot=1; tree[size].val=x;tree[size].rd=rand();return ; } tree[k].tot++; if(tree[k].val==x) tree[k].recy++; else if(x < tree[k].val) insert( ls, x); else insert( rs , x ); } inline void LeftRotate(int &k) { int R=tree[k].r; tree[k].r=tree[R].l; tree[R].l=k; tree[R].tot=tree[k].tot; update(k);k=R; } inline void RightRotate(int &k) { int R=tree[k].l; tree[k].l=tree[R].r; tree[R].r=k; tree[R].tot=tree[k].tot; update(k);k=R; } inline void del(int &k,int x) { if(!k) return ; if(tree[k].val==x) { if(tree[k].recy>1) {tree[k].recy-=1,tree[k].tot-=1;return; } if(tree[k].l*tree[k].r==0) k=tree[k].l+tree[k].r; else if(tree[ls].rd<tree[rs].rd) RightRotate(k),del(k,x); else LeftRotate(k),del(k,x); } else if(x>tree[k].val) tree[k].tot--,del(rs,x); else tree[k].tot--,del(ls,x); } int atrank(int &k,int x) { if(k==0) return 0; if(tree[k].val==x) return tree[ls].tot+1; if(tree[k].val<x) return atrank(rs,x)+tree[ls].tot+tree[k].recy; else return atrank(ls,x); } int rerand(int k,int x) { if(k==0) return 0; if(x<=tree[ls].tot) return rerand(ls,x); else if(x>tree[ls].tot+tree[k].recy) return rerand(rs,x-tree[ls].tot-tree[k].recy); else return tree[k].val; } void pred(int k,int x) { if(k==0) return ; if(tree[k].val<x) ans=k,pred(rs,x); else pred(ls,x); } void succ(int &k,int x) { if(k==0) return ; if(tree[k].val>x) ans=k,succ(ls,x); else succ(rs,x); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif int n=read(); while(n--) { int opt=read(),x=read();ans=0; if(opt==1) insert(root,x); if(opt==2) del(root,x); if(opt==3) printf("%d ",atrank(root,x)); if(opt==4) printf("%d ",rerand(root,x)); if(opt==5) {pred(root,x);printf("%d ",tree[ans].val);} if(opt==6) {succ(root,x);printf("%d ",tree[ans].val);} } }
FHQ Treap

#include<iostream> #include<cstdio> #include<cstring> #include<ctime> #include<cstdlib> using namespace std; #define ls T[now].ch[0] #define rs T[now].ch[1] const int MAXN=1e6+10; inline char nc() { static char buf[MAXN],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin),p1==p2)?EOF:*p1++; } inline int read() { char c=nc();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();} while(c>='0'&&c<='9'){x=x*10+c-'0',c=nc();} return x*f; } struct node { int ch[2],val,siz,pri; }T[MAXN]; int tot=0; int x,y,z,root=0; int newnode(int v) { T[++tot].siz=1; T[tot].val=v; T[tot].pri=rand(); return tot; } void update(int now) { T[now].siz=T[ls].siz+T[rs].siz+1; } void split(int now,int k,int &x,int &y) { if(!now) {x=y=0;return ;} if(T[now].val<=k) x=now,split(rs,k,rs,y); else y=now,split(ls,k,x,ls); update(now); } int merge(int x,int y) { if(!x||!y) return x+y; if(T[x].pri<T[y].pri) { T[x].ch[1]=merge(T[x].ch[1],y); update(x); return x; } else { T[y].ch[0]=merge(x,T[y].ch[0]); update(y); return y; } } int kth(int now,int x) { while(1) { if(T[ls].siz>=x) now=ls; else if(T[ls].siz+1==x) return now; else x-=T[ls].siz+1,now=rs; } } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif srand((unsigned)time(NULL)); int n=read(); while(n--) { int opt=read(),val=read(); if(opt==1) { split(root,val,x,y); root=merge( merge(x,newnode(val)),y ); } else if(opt==2) { split(root,val,x,z); split(x,val-1,x,y); y=merge(T[y].ch[0],T[y].ch[1]); root=merge( merge(x,y) ,z); } else if(opt==3) { split(root,val-1,x,y); printf("%d ",T[x].siz+1); root=merge(x,y); } else if(opt==4) { printf("%d ",T[kth(root,val)].val); } else if(opt==5) { split(root,val-1,x,y); printf("%d ",T[kth(x,T[x].siz)].val); root=merge(x,y); } else if(opt==6) { split(root,val,x,y); printf("%d ",T[kth(y,1)].val); root=merge(x,y); } } return 0; } FHQ Treap
Trie树
01 Trie
http://www.cnblogs.com/zwfymqz/p/8440398.html

#include<cstdio> #include<cmath> #include<algorithm> using namespace std; const int MAXN=1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } #define debug(x) printf("%d",x); struct node { int val,ch[2]; node(){val=ch[0]=ch[1]=0;} void clear(){val=ch[0]=ch[1]=0;} }T[MAXN]; int a[MAXN],root=0,tot=0; void Insert(int v) { int now=root; for(int i=31;i>=0;i--) { int opt=(v&(1<<i))?1:0; if(!T[now].ch[opt]) T[now].ch[opt]=++tot; now=T[now].ch[opt]; T[now].val++; } } void Delet(int v) { int now=root; for(int i=31;i>=0;i--) { int opt=(v&(1<<i))?1:0; now=T[now].ch[opt]; T[now].val--; } } int Query(int v) { int ans=0,now=root; for(int i=31;i>=0;i--) { int opt=(v&(1<<i))?1:0; if(T[T[now].ch[opt^1]].val) ans+=1<<i,now=T[now].ch[opt^1]; else now=T[now].ch[opt]; } return ans; } int main() { freopen("a.in","r",stdin); int Test=read(); while(Test--) { int N=read(); for(int i=1;i<=N;i++) a[i]=read(); for(int i=1;i<=4*N;i++) T[i].clear(); for(int i=1;i<=N;i++) Insert(a[i]); int ans=0; for(int i=1;i<=N;i++) { for(int j=1;j<i;j++) { Delet(a[i]);Delet(a[j]); ans=max(ans,Query(a[i]+a[j])); Insert(a[i]);Insert(a[j]); } } printf("%d ",ans); } return 0; }
杂类算法
树上倍增
https://www.luogu.org/problem/show?pid=3379

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 using namespace std; 6 const int MAXN=1000001; 7 inline void read(int &n) 8 { 9 char c=getchar();bool flag=0;n=0; 10 while(c<'0'||c>'9') c=='-'?flag=1,c=getchar():c=getchar(); 11 while(c>='0'&&c<='9') n=n*10+c-48,c=getchar();flag==1?n=-n:n=n; 12 } 13 struct node 14 { 15 int u,v,nxt; 16 }edge[MAXN]; 17 int head[MAXN]; 18 int num=1; 19 inline void add_edge(int x,int y) 20 { 21 edge[num].u=x; 22 edge[num].v=y; 23 edge[num].nxt=head[x]; 24 head[x]=num++; 25 } 26 int deep[MAXN]; 27 int f[MAXN][21]; 28 int n,m,root; 29 int dfs(int now) 30 { 31 for(int i=head[now];i!=-1;i=edge[i].nxt) 32 if(deep[edge[i].v]==0) 33 deep[edge[i].v]=deep[now]+1,f[edge[i].v][0]=now,dfs(edge[i].v); 34 } 35 int pre() 36 { 37 for(int i=1;i<=19;i++) 38 for(int j=1;j<=n;j++) 39 f[j][i]=f[f[j][i-1]][i-1]; 40 } 41 int LCA(int x,int y) 42 { 43 if(deep[x]<deep[y]) swap(x,y); 44 for(int i=19;i>=0;i--) 45 if(deep[f[x][i]]>=deep[y]) 46 x=f[x][i]; 47 if(x==y) return x; 48 for(int i=19;i>=0;i--) 49 if(f[x][i]!=f[y][i]) 50 x=f[x][i],y=f[y][i]; 51 return f[x][0]; 52 } 53 int main() 54 { 55 memset(head,-1,sizeof(head)); 56 read(n);read(m);read(root); 57 for(int i=1;i<=n-1;i++) 58 { 59 int x,y; 60 read(x);read(y);add_edge(x,y);add_edge(y,x); 61 } 62 deep[root]=1; 63 dfs(root); 64 pre(); 65 for(int i=1;i<=m;i++) 66 { 67 int x,y; 68 read(x);read(y); 69 printf("%d ",LCA(x,y)); 70 } 71 return 0; 72 }
ST表
https://www.luogu.org/problem/show?pid=3865

// luogu-judger-enable-o2 #include<cstdio> #include<algorithm> #define max(a,b) (a<b?b:a) #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<19,stdin),p1==p2)?EOF:*p1++) char buf[1<<19],*p1=buf,*p2=buf; const int MAXN=1e5+10; inline int read() { char c=getchar();register int x=0; while(c<'0'||c>'9')c=getchar(); while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar(); return x; } char obuf[1<<24],*O=obuf; void print(int x) { if(x>9) print(x/10); *O++=x%10+'0'; } int N,M; int f[MAXN][22]; int log2[MAXN]; int Query(int l,int r) { int k=log2[r-l+1]; return max(f[l][k],f[r-(1<<k)+1][k]); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif N=read();M=read(); for(int i=1;i<=N;i++) f[i][0]=read(); for(int i=2;i<=N;i++) log2[i]=log2[i>>1]+1; for(register int j=1;j<=17;j++) for(register int i=1;i<=N&&i+(1<<j)-1<=N;i++) f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); while(M--) { int l=read(),r=read(); print(Query(l,r)); *O++=' '; } fwrite(obuf,O-obuf,1,stdout); return 0; }
点分治
给定一棵有n个点的树
询问树上距离为k的点对是否存在

#include<iostream> #include<cstdio> #include<cstring> #include<cmath> using namespace std; const int MAXN=1e6+10; const int INF=1e7+10; inline char nc() { static char buf[MAXN],*p1=buf,*p2=buf; return p1==p2&&(p2=(p1=buf)+fread(buf,1,MAXN,stdin),p1==p2)?EOF:*p1++; } inline int read() { char c=nc();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=nc();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=nc();} return x*f; } struct node { int u,v,w,nxt; }edge[MAXN]; int head[MAXN]; int num=1; inline void AddEdge(int x,int y,int z) { edge[num].u=x; edge[num].v=y; edge[num].w=z; edge[num].nxt=head[x]; head[x]=num++; } int F[MAXN],sum,siz[MAXN],vis[MAXN],root=0,cnt=0,deep[MAXN],can[MAXN]; struct Ans { int v,id; }tot[MAXN]; void GetRoot(int now,int fa) { siz[now]=1; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(vis[edge[i].v]||edge[i].v==fa) continue; GetRoot(edge[i].v,now); siz[now]+=siz[edge[i].v]; F[now]=max(F[now],siz[edge[i].v]); } F[now]=max(F[now],sum-F[now]); if(F[now]<F[root]) root=now; } void GetDeep(int now,int fa,int NowDeep,int num) { int cur=0; tot[++cnt].v=deep[now]; tot[cnt].id=num; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(vis[edge[i].v]||edge[i].v==fa) continue; deep[edge[i].v]=deep[now]+edge[i].w; if(NowDeep!=1) GetDeep(edge[i].v,now,NowDeep+1,num); else GetDeep(edge[i].v,now,NowDeep+1,cur++); } } void Work(int now) { cnt=0;deep[now]=0; GetDeep(now,0,1,1); for(int i=1;i<=cnt;i++) for(int j=i+1;j<=cnt;j++) if(tot[i].id!=tot[j].id) can[tot[i].v+tot[j].v]=1; else can[tot[i].v]=1,can[tot[j].v]=1; } void Solve(int now) { Work(now); vis[now]=1; for(int i=head[now];i!=-1;i=edge[i].nxt) { if(vis[edge[i].v]) continue; root=0; sum=siz[edge[i].v]; GetRoot(edge[i].v,0); Solve(edge[i].v); } } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif memset(head,-1,sizeof(head)); int N=read(),M=read(); for(int i=1;i<=N-1;i++) { int x=read(),y=read(),z=read(); AddEdge(x,y,z); AddEdge(y,x,z); } root=0; F[0]=INF; sum=N; GetRoot(1,0); Solve(root); for(int i=1;i<=M;i++) { int p=read(); if(can[p]) printf("AYE "); else printf("NAY "); } return 0; }
主席树

// luogu-judger-enable-o2 // luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<algorithm> #define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++) char buf[1<<21],*p1=buf,*p2=buf; using namespace std; const int MAXN=4*1e6+10; inline int read() { char c=getchar();register int x=0; while(c<'0'||c>'9')c=getchar(); while(c>='0'&&c<='9')x=x*10+c-'0',c=getchar(); return x; } char obuf[1<<24],*O=obuf; void print(int x) { if(x>9) print(x/10); *O++=x%10+'0'; } int N,M; int a[MAXN],date[MAXN]; #define ls(x) T[x].ls #define rs(x) T[x].rs struct node { int siz,ls,rs; }T[MAXN]; int root[MAXN],tot=0; void Insert(int pre,int &now,int l,int r,int pos) { if(!now) now=++tot; T[now].siz=T[pre].siz+1; if(l==r) return ; int mid=(l+r)>>1; if(pos<=mid) T[now].rs=T[pre].rs,Insert(T[pre].ls,T[now].ls,l,mid,pos); else T[now].ls=T[pre].ls,Insert(T[pre].rs,T[now].rs,mid+1,r,pos); } int Query(int pre,int now,int l,int r,int k) { if(l==r) return l; int left=T[ls(now)].siz-T[ls(pre)].siz; int mid=(l+r)>>1; if(k>left) return Query(T[pre].rs,T[now].rs,mid+1,r,k-left); else return Query(T[pre].ls,T[now].ls,l,mid,k); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif N=read();M=read(); for(int i=1;i<=N;i++) date[i]=a[i]=read(); sort(date+1,date+N+1); int num=unique(date+1,date+N+1)-date-1; for(int i=1;i<=N;i++) a[i]=lower_bound(date+1,date+num+1,a[i])-date; for(int i=1;i<=N;i++) Insert(root[i-1],root[i],1,num,a[i]); for(int i=1;i<=M;i++) { int l=read(),r=read(),k=read(); print(date[Query(root[l-1],root[r],1,num,k)]); *O++=' '; } fwrite(obuf,O-obuf,1,stdout); return 0; }
排序
归并排序

1 #include<cstdio> 2 #include<iostream> 3 #include<cmath> 4 using namespace std; 5 const int MAXN=100001; 6 inline int read() 7 { 8 char c=getchar();int x=0,flag=1; 9 while(c<'0'||c>'9') {if(c=='-') flag=-1;c=getchar();} 10 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*flag; 11 } 12 int n; 13 int a[MAXN]; 14 int tmp[MAXN]; 15 void Sort(int l,int r) 16 { 17 if(l==r) return ; 18 int mid=l+r>>1; 19 Sort(l,mid);Sort(mid+1,r); 20 int nowl=l,nowr=mid+1,nowpos=l; 21 while(nowl<=mid&&nowr<=r) 22 { 23 if(a[nowl]<=a[nowr]) tmp[nowpos++]=a[nowl],nowl++; 24 else tmp[nowpos++]=a[nowr],nowr++; 25 } 26 while(nowl<=mid) tmp[nowpos++]=a[nowl],nowl++; 27 while(nowr<=r) tmp[nowpos++]=a[nowr],nowr++; 28 for(int i=l;i<=r;i++) a[i]=tmp[i]; 29 } 30 int main() 31 { 32 n=read(); 33 for(int i=1;i<=n;i++) a[i]=read(); 34 Sort(1,n); 35 for(int i=1;i<=n;i++) printf("%d ",a[i]); 36 return 0; 37 }
高精度
高精加

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<stdlib.h> 6 #include<ctime> 7 using namespace std; 8 const int MAXN=100001; 9 inline int read() 10 { 11 char c=getchar();int f=1,x=0; 12 while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();} 13 while(c>='0'&&c<='9') x=x*10+c-48,c=getchar();return x*f; 14 } 15 char a[MAXN],b[MAXN],c[MAXN]; 16 int la,lb,x=0; 17 int main() 18 { 19 scanf("%s%s",a+1,b+1); 20 la=strlen(a+1);lb=strlen(b+1); 21 for(int i=1;i<=max(la,lb);i++) 22 c[i]+=(a[i]+b[i]+x)%10,x=(a[i]+b[i]+x)/10; 23 c[max(la,lb)+1]=x; 24 bool flag=0; 25 for(int i=max(la,lb)+1;i>=1;i--) 26 if(c[i]!=0) 27 { 28 for(int j=i;j>=1;j--) printf("%d",c[j]); 29 return 0; 30 } 31 printf("0"); 32 return 0; 33 }
数论
Lucas定理
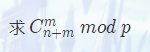

#include<cstdio> #include<algorithm> #include<cmath> #include<map> #define int long long using namespace std; const int MAXN = 4 * 1e5 + 10, mod = 100003; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int T, N, M, P; int fac[MAXN] = {1}; int fastpow(int a, int p, int mod) { int base = 1; while(p) { if(p & 1) base = (base % mod * a % mod) % mod; a = (a % mod * a % mod) % mod; p >>= 1; } return base % mod; } int inv(int a, int p) { return fastpow(a, p - 2, p); } int C(int N, int M, int P) { if(M > N) return 0; return fac[N] % P * inv(fac[M] * fac[N - M], P); } int Lucas(int N, int M, int P) { if(!N || !M) return 1; return Lucas(N / P, M / P, P) * C(N % P, M % P, P); } main() { //freopen("a.in", "r", stdin); T = read(); while(T--) { int N = read(), M = read(), P = read(); N = N + M; for(int i = 1; i <= 2 * 1e5; i++) fac[i] = (i * fac[i - 1]) % P; printf("%lld ", Lucas(N, M, P) % P); } }
高斯消元
https://www.luogu.org/problemnew/show/P3389

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #define swap(x, y) x ^= y, y ^= x, x ^= y const int MAXN= 102; double A[MAXN][MAXN]; double Ans[MAXN]; int N; void Guess() { for(int i = 1; i <= N; i++) { int mx = i; for(int j = i + 1; j <= N; j++) if(A[j][i] > A[mx][i]) swap(mx, j); if(A[i][i] == 0) {printf("No Solution ");return ;} for(int j = i + 1; j <= N; j++) { double tmp = A[j][i] / A[i][i]; for(int k = i + 1; k <= N + 1; k++) A[j][k] -= tmp * A[i][k]; } } for(int i = N; i >= 1; i--) { Ans[i] = A[i][N + 1] / A[i][i]; for(int j = i; j >= 1; j--) A[j][N + 1] -= A[j][i] * Ans[i]; } for(int i = 1; i <= N; i++) printf("%.2lf ", Ans[i]); } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif scanf("%d", &N); for(int i = 1; i <= N; i++) for(int j = 1; j <= N + 1; j++) scanf("%lf", &A[i][j]); Guess(); return 0; }
莫比乌斯反演
FGD正在破解一段密码,他需要回答很多类似的问题:对于给定的整数a,b和d,有多少正整数对x,y,满足x<=a,y<=b,并且gcd(x,y)=d。作为FGD的同学,FGD希望得到你的帮助。

// luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> #define int long long using namespace std; const int MAXN=1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<'0'||c>'9'){if(c=='-')f=-1;c=getchar();} while(c>='0'&&c<='9'){x=x*10+c-'0';c=getchar();} return x*f; } int N; int vis[MAXN],prime[MAXN],mu[MAXN],tot=0; void GetMu() { vis[1]=1;mu[1]=1; for(int i=1;i<=N;i++) { if(!vis[i]) prime[++tot]=i,mu[i]=-1; for(int j=1;j<=tot&&i*prime[j]<=N;j++) { vis[i*prime[j]]=1; if(i%prime[j]==0) {mu[i*prime[j]]=0;break;} else mu[i*prime[j]]=-mu[i]; } } for(int i=1;i<=N;i++) mu[i]+=mu[i-1]; } main() { #ifdef WIN32 freopen("a.in","r",stdin); #else #endif N=1e6; GetMu(); int QWQ=read(); while(QWQ--) { int n=read(),m=read(),k=read(),ans=0; int limit=min(n/k,m/k); int nxt=0; for(int i=1;i<=limit;i=nxt+1) nxt=min(n/(n/i),m/(m/i)), ans+=(mu[nxt]-mu[i-1])*((n/k)/i)*((m/k)/i); printf("%lld ",ans); } return 0; }
线性基

//http://acm.hdu.edu.cn/showproblem.php?pid=3949 #include<bits/stdc++.h> #define LL long long using namespace std; const int MAXN = 67, B = 51; inline LL read() { char c = getchar(); LL x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M; struct LinearBasis { #define LL long long LL P[63]; int B; LinearBasis() { B = 62; memset(P, 0, sizeof(P)); } void clear() { memset(P, 0, sizeof(P)); } void insert(LL val) { for(int i = B; i >= 0; i--) { if(!(val >> i & 1)) continue; if(P[i]) {val ^= P[i]; continue;} for(int j = 0; j < i; j++) if(val >> j & 1) val ^= P[j]; for(int j = i + 1; j <= B; j++) if(P[j] >> i & 1) P[j] ^= val; P[i] = val; return ; } } LL QueryMax() { LL ans = 0; for(int i = 0; i <= B; i++) ans ^= P[i]; return ans; } LL QueryKth(LL k) { std::vector<int> v; for(int i = 0; i <= B; i++) if(P[i]) v.push_back(P[i]); if(v.size() != N) k--; if(k > ((1ll << v.size()) - 1)) return -1; LL ans = 0; for(int i = 0; i < v.size(); i++) if(k >> i & 1) ans ^= v[i]; return ans; } #undef LL }Ba; void solve() { N = read(); for(int i = 1; i <= N; i++) Ba.insert(read()); M = read(); while(M--) cout << Ba.QueryKth(read()) << endl; } signed main() { int T = read(); for(int i = 1; i <= T; i++) Ba.clear(), printf("Case #%d: ", i), solve(); return 0; }
多项式
FFT

// luogu-judger-enable-o2 #include<cstdio> #include<algorithm> #include<cmath> #define Pi acos(-1) using namespace std; const int MAXN = 4 * 1e6 + 10; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } int N, M, limit = 1, L; struct complex { double x, y; complex(double xx = 0, double yy = 0) {x = xx, y = yy;} complex operator + (const complex &rhs) { return complex(x + rhs.x, y + rhs.y); } complex operator - (const complex &rhs) { return complex(x - rhs.x, y - rhs.y); } complex operator * (const complex &rhs) { return complex(x * rhs.x - y * rhs.y, x * rhs.y + y * rhs.x); } }a[MAXN], b[MAXN]; int r[MAXN]; void FFT(complex *A, int type) { for(int i = 0; i < limit; i++) if(i < r[i]) swap(A[i], A[r[i]]); for(int mid = 1; mid < limit; mid <<= 1) { complex Wn = complex(cos(Pi / mid), type * sin(Pi / mid)); for(int R = mid << 1, j = 0; j < limit; j += R) { complex w = complex(1, 0); for(int k = 0; k < mid; k++, w = w * Wn) { complex x = A[j + k], y = w * A[j + k +mid]; A[j + k] = x + y, A[j + k + mid] = x - y; } } } } int main() { #ifdef WIN32 freopen("a.in", "r", stdin); #endif N = read(); M = read(); for(int i = 0; i <= N; i++) a[i].x = read(); for(int i = 0; i <= M; i++) b[i].x = read(); while(limit <= N + M) limit <<= 1, L++; for(int i = 0; i <= limit; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (L - 1)); FFT(a, 1);FFT(b, 1); for(int i = 0; i < limit; i++) a[i] = a[i] * b[i]; FFT(a, -1); for(int i = 0; i <= N + M; i++) printf("%d ", (int)(a[i].x / limit + 0.5)); return 0; }
NTT

// luogu-judger-enable-o2 // luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<algorithm> #define getchar() (p1 == p2 && (p2 = (p1 = buf) + fread(buf, 1, 1<<21, stdin), p1 == p2) ? EOF : *p1++) #define swap(x,y) (x ^= y, y ^= x, x ^= y) #define mul(a, b) 1ll * a * b % P #define add(a, b) (a + b >= P ? a + b - P : a + b) #define dec(a, b) (a - b < 0 ? a - b + P : a - b) #define rg register using namespace std; const int MAXN = 4 * 1e6, P = 998244353, Gi = 3; char buf[1<<21], *p1 = buf, *p2 = buf; inline int read() { char c = getchar(); int x = 0, f = 1; while(c < '0' || c > '9') {if(c == '-') f = -1; c = getchar();} while(c >= '0' && c <= '9') x = x * 10 + c - '0', c = getchar(); return x * f; } char obuf[1<<24], *O=obuf; void print(int x) { if(x > 9) print(x / 10); *O++= x % 10 + '0'; } inline int fastpow(int a, int k) { int base = 1; while(k) { if(k & 1) base = mul(a, base); a = mul(a, a); k >>= 1; } return base % P; } int N, r[MAXN], A[MAXN], B[MAXN], Og[MAXN], F[MAXN], Q[MAXN], G[MAXN], R[MAXN]; inline void NTT(int *A, int type, int len) { int limit = 1, L = 0; while(limit < len) limit <<= 1, L++; for(rg int i = 0; i < limit; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) << (L - 1)); for(rg int i = 0; i < limit; i++) if(i < r[i]) swap(A[i], A[r[i]]); for(rg int mid = 1; mid < limit; mid <<= 1) { int R = mid << 1; int W = fastpow(Gi, (P - 1) / R); Og[0] = 1; for(rg int j = 1; j < mid; j++) Og[j] = mul(Og[j - 1], W); for(rg int j = 0; j < limit; j += R) { for(rg int k = 0; k < mid; k++) { const int x = A[j + k], y = mul(Og[k], A[j + k + mid]); A[j + k] = add(x, y), A[j + k + mid] = dec(x, y); } } } if(type == -1) { std::reverse(&A[1], &A[limit]); for(int i = 0, inv = fastpow(len , P - 2); i < limit; i++) A[i] = 1ll * A[i] * inv % P; } } void Inv(int *a, int *b, int len) {// a要求的多项式 b逆元 len:要求的逆元的长度 if(len == 1) { b[0] = fastpow(a[0], P - 2); return ; } Inv(a, b, len >> 1); for(rg int i = 0; i < len; i++) A[i] = a[i], B[i] = b[i]; NTT(A, 1, len << 1); NTT(B, 1, len << 1); for(rg int i = 0; i < (len << 1); i++) A[i] = mul(mul(A[i], B[i]), B[i]) ; NTT(A, -1, len << 1); for(rg int i = 0; i < len; i++) b[i] = (1ll * (b[i] << 1) % P + P - A[i] ) % P; } void Mul(int *a, int *b, int *c, int N) { int len; for(len = 1; len < N; len <<= 1); NTT(a, 1, len); NTT(b, 1, len); for(int i = 0; i < len; i++) c[i] = 1ll * a[i] * b[i] % P; NTT(c, -1, len); } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif int N = read(), M = read(); for(int i = 0; i <= N; i++) F[i] = read(); for(int i = 0; i <= M; i++) G[i] = read(); /*reverse(F, F + N + 1); reverse(G, G + M + 1);*/ Mul(F, G, R, N + M + 1); for(int i = 0; i <= N + M; i++) print(R[i]), *O++ = ' '; fwrite(obuf, O-obuf, 1 , stdout); return 0; }
