我理解的高等代数3——线性变换

3我理解的高等代数3——线性变换

线性变换

第一节我们介绍了线性空间，他就是一个方格纸。

第二节我们介绍了坐标系变换中，基变换和坐标之间的关系。

接下来让我们考虑在坐标系变换中的变换本身这个东西。

让我们继续回到我们熟悉的情形，让我们重新描述这个过程。

通过一个变换或者说乘以一个矩阵A，我们使得原来的方格纸发生了变化。变化后的结果还是一个方格纸。 原来的一些向量大多数发生了相应的变化，但是有一些向量方向没有发生变化只是长度发生了变化。

我们发现这个变化是有一些特点的，

• 1 就是变化后并没有改变方格纸这个基本形状。按着数学的语言描述，那就是这个变换使得一个线性空间变成了一个新的线性空间。
• 2 整个变换对于原来的向量之间的对应关系是没有发生变化的。用数学的语言描述就是 它保持了原来元素的加法和数量乘法。

其实，这个变换就是一个特殊的映射，是一个满足上述两条性质的特殊的映射。

线性变换空间

那么我们可以得到很多具有上面性质的变换，我们如果把每一个变换记一个数学符号，比如\(\mathscr{A},\mathscr{B},\cdots\)

我们想，这些元素是不是也符合线性空间的要求，组成一个线性空间。事实上，这个变换时能够组成线性空间的。

既然是一个线性空间，那么就能得到这个空间的零元素和单位元。我们一般记为\(0,\epsilon\)

同时我们还可以在这些元素的基础上定义运算，乘法，加法，数乘，逆变换。多形式运算。

线性变换与向量的像

我们说，线性变换是一个特殊的映射，那么对于集合A（也就是定义域）在集合B（也就是值域）都会有一个元素与之对应。

我们设有一组基为\([i,j]\),那我们记变换前的元素为\(a\),其坐标在基\([i,j]\)下的坐标为\((x_1,x_2)\) ，

,那么变换后的元素\(\mathcal{A}a\)在基\([i,j]\)下的坐标\((y_1，y_2)\)就有这样的一个对应关系

\[\left ( \begin{matrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \\ \end{matrix} \right ) =A \left ( \begin{matrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{matrix} \right ) \]

线性变换与基

在一组基下，我们能够描述一个线性变换,这样的一个变换对应着一个矩阵

\[\mathscr{A}\varepsilon_i=\alpha_i \ \ \ \ A e =a \]

那么我们接下来想问一个问题，如果换一组基，这个变换会是怎样的形式，它和原来的基下的变换有什么关系。

首先我们有两组基，不妨记为 \([\varepsilon_1,\varepsilon_2]\)和\([\eta_1,\eta_2]\)

然后我们有一个从基 \([\varepsilon_1,\varepsilon_2]\)到基的\([\eta_1,\eta_2]\)过渡矩阵是\(X\)。

这里再让我们回顾一下过渡矩阵，这个过渡矩阵其实就是新的基\([\eta_1,\eta_2]\)在原来的基下\([\varepsilon_1,\varepsilon_2]\)面的坐标\((a,b),(c,d)\)，我们把这个坐标放在一起组成了一个矩阵\(X\)

\[X = \left( \begin{array}{1} a, & c\\ b , &d \end{array} \right ) \]

这个矩阵第一列的元素是新基\(\eta_1\)在下\([\varepsilon_1,\varepsilon_2]\)的坐标，第二列的元素是新基\(\eta_2\)的在下的坐\([\varepsilon_1,\varepsilon_2]\)标

我们有\([\eta_1,\eta_2]=[\varepsilon_1,\varepsilon_2]X\)

然后我们来看一下这两个变换，用矩阵形式表示有

\[\mathscr{A}\varepsilon_i= [\varepsilon_1,\varepsilon_2]A \\ \mathscr{A}\eta_i= [\eta_1,\eta_2] B \]

我们知道变换会保持原来元素的关系，于是变换后我们仍然有

\[\mathscr{B}\eta_i=\mathscr{A}\varepsilon_i X \]

用矩阵形式表示就是

\[[\eta_1,\eta_2] B= [\varepsilon_1,\varepsilon_2]A X \]

我们将基从基 \([\varepsilon_1,\varepsilon_2]\)到基的\([\eta_1,\eta_2]\)过渡矩阵\(X\) 的对应关系\([\eta_1,\eta_2]=[\varepsilon_1,\varepsilon_2]X\)带入得到

\[[\varepsilon_1,\varepsilon_2]X B= [\varepsilon_1,\varepsilon_2]A X \]

可以得到

\[B =X^{-1}AX \]

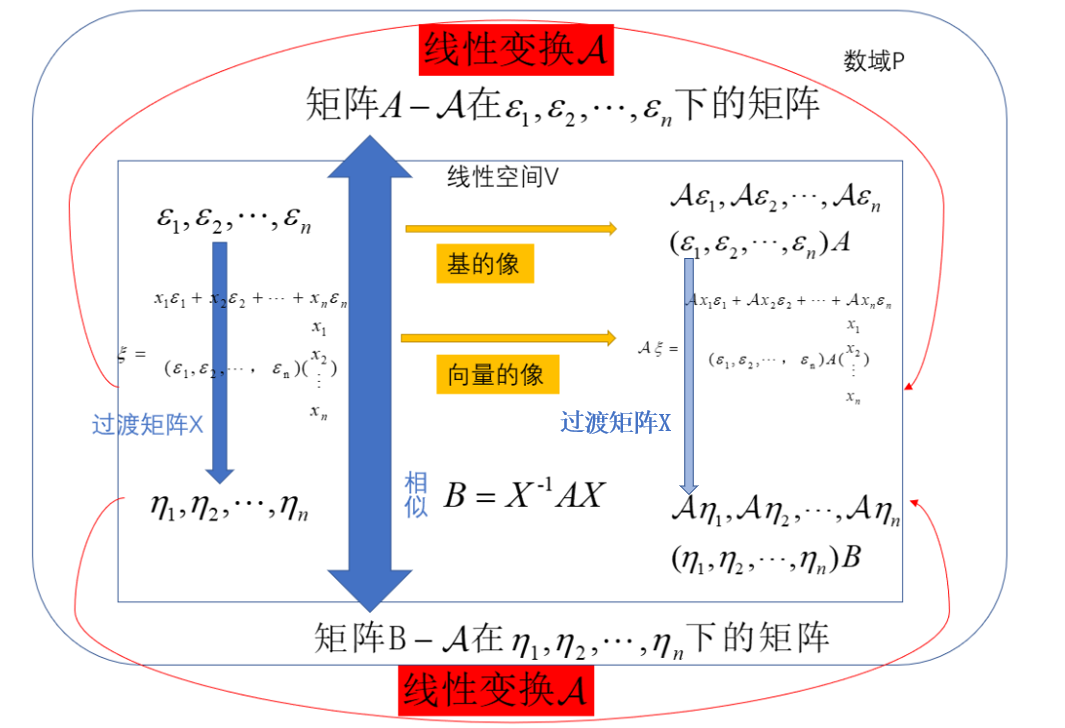
整个过程的推导关键在于，基向量通过线性变换后仍然存在着过渡矩阵的一个变化关系。

相似

如果两个矩阵有着我们上面推导出的关系 ，即

设\(A、B\)是数域\(P\)上两个\(n\)级矩阵，如果可以找到数域\(P\)上的\(n\)级可逆矩阵\(X\)，使得\(B=X^{-1}AX\)，就说\(A\)相似于\(B\)，记作\(A \sim B\)