本篇文章主要详解位运算的相关问题,以及解析python语言在求解该问题上的不方便。
涉及知识点:
1.原码,补码,反码的知识
2.与,或,非,异或,左移,右移,负数右移的相关知识
3.python数据类型
我们从一个题目说起,该题来自于《剑指offer》。
题目描述:输入一个整数,输出该数二进制表示中1的个数。其中负数用补码表示。
解题思路:首先要意识到这是一道考察位运算的题目,如果没有这个意识,很可能开始循环除2,这样也是可以做的,但是就是要注意负数的情况,这个方法比较繁琐,就不展开了。既然是位运算的题目,不免涉及到移位,与,或,异或等运算符的使用。
解法1:我们很自然的想到,将输入的n与1相与,检查低位是否为1,然后不断右移n,直到n为0为止。但这种思路其实是针对正数的。右移相当于除2,1/2为0,而-1/2为-1。如果在判断循环结束时只判断n是否为0,就会进入死循环。但是即使加了-1的判断,程序没了死循环,由于符号位会跟着右移,在-1时停止循环,其实会损失掉很多靠近符号位的1,它们被当成是右移的1了。这时还需要增加一个循环次数的判断,显然非常麻烦。解法1的代码省略。
解法2:既然n左移很麻烦,那我们用一个flag设置为1,不断左移,去检查n每一个是否为1。但是在python语言中,python3中的int是没有范围的。flag不会左移到0这个边界,而是会不断拓展。这时候就需要设定flag的左移次数。复杂度就是n二进制表示的位数。
介绍下python3的数据类型。
python3支持三种不同的数值类型。
- 整型int,没有限制大小,可以当作long来使用,但实际上机器内存有限,不能无限制使用。当然整型又分为二,八,十,十六四种进制表示。
- 浮点型float
- 复数complex,实部和虚部构成,且这两个部分均为浮点型。
强调python3是因为,python2是限定了位数了,32位机器是32位表示,64位机器是64位表示,超过了这个范围就是long类型,而且是自动转换为long类型。
python还有将十进制转为二进制的函数,bin()。然后我们直接调用再计算1字符的个数可不可以呢?bin(n).count('1')。对于正数是可以的,但是负数,在python中返回的字符串是'-0b10'。没办法看来调包不行,其实python既然没有限定多少位来表示整数,也就很难显示符号位的位置了。
# 解法2
# -*- coding:utf-8 -*-
class Solution:
def NumberOf1(self, n):
count = 0
flag = 1
i = 0
while i<=31:
if (flag&n)!=0 :
count+=1
flag=flag<<1
i+=1
return count
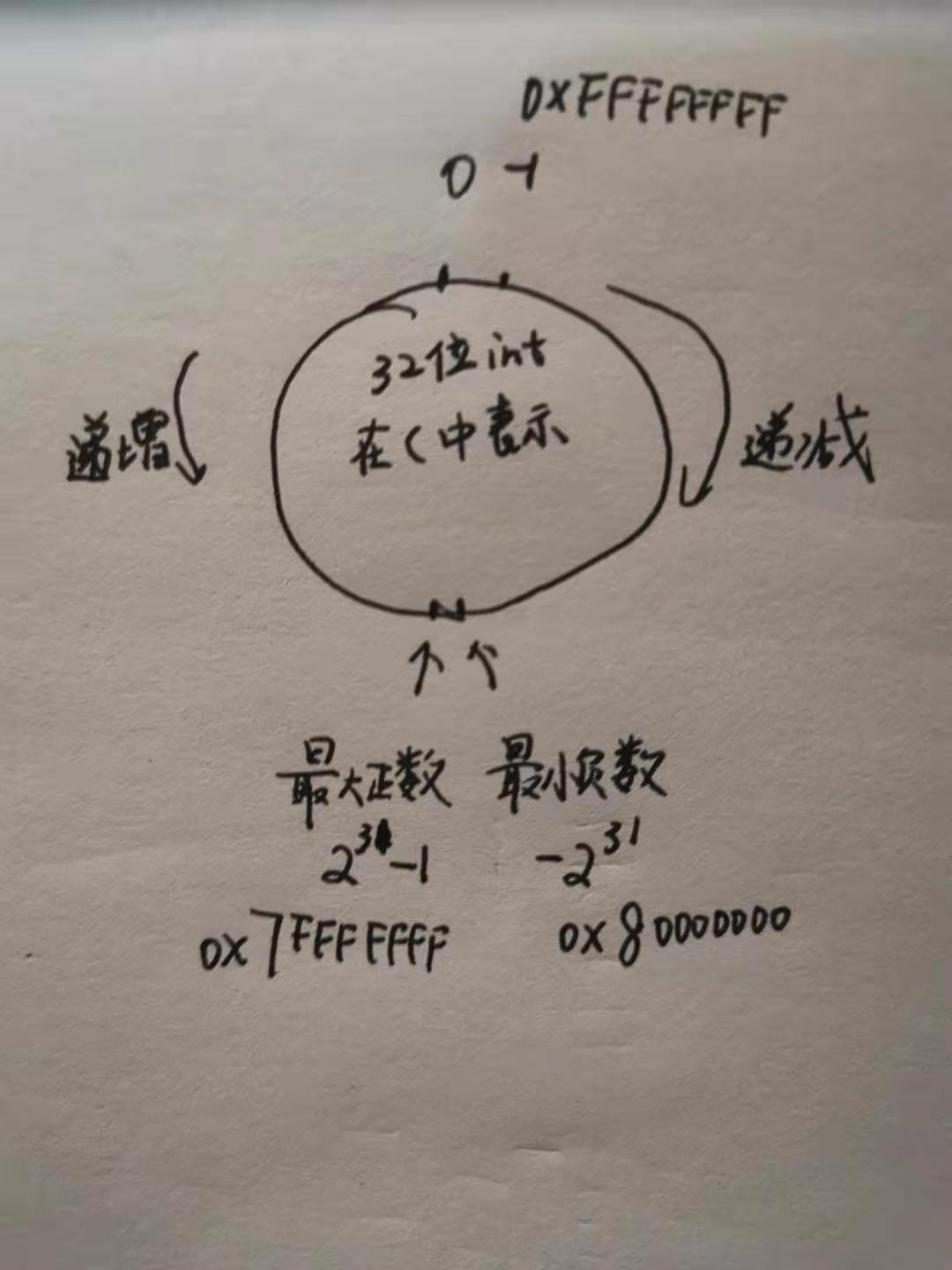
解法3:通过n&(n-1)的观察,可以得到更加简单求解方法。比如10,二进制表示为1010,10-1=9,9的二进制是1001,可以观察到-1操作,会使得二进制最右边的1置零,1右边的所有0置1。于是n&(n-1)的操作就是将二进制表示中的最右边的1置零。我们做几次这个操作,就说明二进制表示中有多少个1。复杂度降到了二进制表示中1的个数。等等,这里的负数会不会出问题呢?对于C来说,不会,我们看下图。当n为最小的负数时,n-1就时最大的正数,此时相与,结果为0,正好和正数的边界条件一样。但是对于python来说,它没有这个圈的说法,没有边界,n-1只会一直缩小,进入死循环。所以我们要加一个边界条件,限定n不能小于最小的负数。图中的几个特殊值,牢记用来做测试。
#解法3
# -*- coding:utf-8 -*-
class Solution:
def NumberOf1(self, n):
count =0
while n>=-0X80000000 and n!=0:
n = n&(n-1)
count+=1
return count
相关题目:
- 判断某个数是否是2的某次方。其实就是判断二进制中是否只含有一个1。使用n&(n-1)就可以做到。
- 判断两个数的二进制,需要多少位变化,才能转换为对方。举例10二进制是1010,13是1101,它们需要3位转换。先异或,再用n&(n-1)求出1的个数即可。