手写二叉排序树（二叉查找树、二叉搜索树）

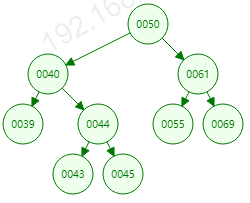
在二叉排序树中,每个根节点只能有左右两个子节点,左子节点比根节点小,右子节点比根节点大(TreeSet中不允许出现相同元素。一些场景下,如果子节点和根节点相同会将子节点放到根节点的右边)。

//二叉搜索树
public class BinarySearchTree<T extends Comparable> {

    private int size;

    private Node root;

    //添加元素
    public boolean add(T data) {
        if (size == 0) {
            root = new Node(data, null);
        } else {
            add(data, root);
        }
        size++;
        return true;
    }

    //递归添加子节点
    private void add(T data, Node root) {
        //调用元素的compareto方法，查看根节点和data的大小关系
        int f = root.data.compareTo(data);
        //如果f大于等于0说明节点大，那应该把数据放在根节点左边。
        //如果f小于0说明节点小数据大，应该把数据放到根节点右边
        Node node = f > 0 ? root.left : root.right;
        //如果根节点的左边或者右边==null表示可以直接往根节点放子节点
        if (node == null) {
            //创建子节点
            Node newNode = new Node(data, root);
            if (f > 0) {
                //放到左边
                root.left = newNode;
            } else {
                //放到右边
                root.right = newNode;
            }
        } else {
            //如果根据点的左边或者右边有元素
            //需要将改元素在次重复判断以上全部步骤。
            add(data, node);
        }
    }


    //打印二叉树查看结果
    public Object[] list() {
        ArrayList<T> list = new ArrayList<>();
        toArray(root, list);
        return list.toArray();
    }

    //递归函数
    private void toArray(Node node, ArrayList list) {
        Node left = node.left;
        //如果有左节点
        if (left != null) {
            toArray(left, list);
        }

        System.out.println(node.data);//打印自身节点
        list.add(node.data);
        //如果有右边节点，一样递归
        Node right = node.right;
        if (right != null) {
            toArray(right, list);
        }

        return;
    }

    public int size() {
        return size;
    }


    //判断节点是否存在
    public boolean contains(T data) {
        if (query(data, root) == null) {
            System.out.println("没有找到");
            return false;
        } else {
            System.out.println("一共寻找了" + x + "次");
            return true;
        }
    }

    int x = 0;//记录树的遍历次数，以检验是否是最优解

    //查询节点
    private Node query(T data, Node node) {
        x++;
        //先找到这个元素的位置
        int i = node.data.compareTo(data);
        //如果==0就是找到了。
        if (i == 0) {
            return node;
        }
        Node left = node.left;
        Node right = node.right;
        //向左查询
        if (i > 0 && left != null) {
            return query(data, left);
        } else if (i < 0 || right != null) {//向右查询
            return query(data, right);
        } else {
            return null;
        }
    }

    /*
     * 删除节点有三种情况
     * 1 被删除的节点无子孙节点，直接删除。
     * 2 被删除的节点只有左子节点或者只有右子节点，需要将左或者右子节点顶替被删除的节点。
     * 3 被删除的节点有左子节点或者右子节点，这种情况有两种方案。
     *   1 从左节点族群中找到最右边的子孙节点。
     *   2 从右节点族群中找到最左边的子孙节点。
     * 二叉树的规则是节点左边的小于节点，节点右边的大于或等于节点。所以找到左边的最右边或者右边
     * 的最左边这两个值是最接近于被删除节点的。我这里取值是左边的最右边
     * */
    public T remove(T data) {
        Node removeNode = query(data, root);
        if (removeNode == null) {
            return null;
        }
        //如果只有一个节点,那么肯定是root节点
        if (size == 1) {
            root = null;
        } else if (removeNode.left == null && removeNode.right == null) {//第一种情况
            //拿到父节点，如果当前节点没有父节点也没有子节点，那么size就是1不会走到这里
            Node removeNodeParent = removeNode.parent;
            //判断当前节点在父节点的左边还是右边，如果父节点比被删除节点大
            //表示被删除的节点在父节点的左边，如果相等或者小于那么被删除的
            //元素在父节点的右边
            int c = removeNodeParent.data.compareTo(removeNode.data);
            if (c > 0) {
                //父节点左孩子置为null
                removeNodeParent.left = null;
            } else {
                //父节点右孩子置为null
                removeNodeParent.right = null;
            }
        } else if (removeNode.left == null || removeNode.right == null) {//第二种情况
            //替代被删除的节点
            Node newChild;
            //被删除的节点有左节点族群
            if (removeNode.left != null) {
                //被删除节点的左节点替代被删除的节点
                newChild = removeNode.left;
                //断开被删除节点与子节点的指针
                removeNode.left = null;
            } else {
                //被删除的节点有右节点族群
                //被删除节点的右节点替代被删除的节点
                newChild = removeNode.right;
                //断开被删除节点与子节点的指针
                removeNode.right = null;
            }
            //如果被删除的节点没有父节点，说明这个节点是根节点
            Node removeNodeParent = removeNode.parent;
            //如果不是根节点。
            if (removeNodeParent != null) {
                //判断当前节点在父节点的左边还是右边，如果父节点比被删除节点大
                //表示被删除的节点在父节点的左边，如果相等或者小于那么被删除的
                //元素在父节点的右边
                int c = removeNodeParent.data.compareTo(removeNode.data);
                if (c > 0) {
                    //将替代节点设为父节点的左孩子
                    removeNodeParent.left = newChild;
                } else {
                    //将替代节点设为父节点的右孩子
                    removeNodeParent.right = newChild;
                }
                //断开被删除节点与父节点的指针
                removeNode.parent = null;
            } else {//如果被删除的节点是根节点，那么被删除节点无论是拥有左节点还是右节点这个节点都是根节点
                root = newChild;
                //根节点不需要父节点
                root.parent = null;
            }
        } else {//第三种情况
            Node newChild = queryLeftInRight(removeNode.left);
            //拿到替换节点的父节点
            Node newChildParent = newChild.parent;
            //查询替换节点在它原本父节点的哪边
            int i = newChildParent.data.compareTo(newChild.data);
            //此操作为了将替换节点从原有的父节点删掉。
            if (i > 0) {
                newChildParent.left = null;
            } else {
                newChildParent.right = null;
            }

            //被删除节点的父节点
            Node removeNodeParent = removeNode.parent;

            //被删除的节点不是根节点
            if (removeNodeParent != null) {
                //判断当前节点在父节点的左边还是右边，如果父节点比被删除节点大
                //表示被删除的节点在父节点的左边，如果相等或者小于那么被删除的
                //元素在父节点的右边
                int c = removeNodeParent.data.compareTo(removeNode.data);
                if (c > 0) {
                    removeNodeParent.left = newChild;
                } else {
                    removeNodeParent.right = newChild;
                }
                //如果被删除节点的左节点不是替代节点
                //则需要将被删除节点的左节点交给替代节点的左节点
                if (removeNode.left != newChild) {
                    newChild.left = removeNode.left;
                }
                //被删除元素的右节点交给替代节点的右节点
                newChild.right = removeNode.right;
                //端口被删除节点与子节点和父节点的指针
                removeNode.parent = null;
                removeNode.left = null;
                removeNode.right = null;
            } else {//被删除的是根节点
                //如果根节点的左边节点不是替代节点则
                //将父节点的左边交给替代节点的左边
                if (root.left != newChild) {
                    newChild.left = root.left;
                }
                //将根节点的右子节点交给替代节点的右边
                newChild.right = root.right;
                //替代节点成为根节点
                root = newChild;

            }

        }

        //长度-1
        size--;
        //返回被删除节点的数据
        return removeNode.data;
    }

    //获取左节点族中最右边的节点
    private Node queryLeftInRight(Node node) {
        if (node.right != null) {
            return queryLeftInRight(node.right);
        }
        return node;
    }

    class Node {
        private T data;//节点数据
        private Node left;//左边的孩子
        private Node right;//右边的孩子
        private Node parent;//父节点

        public Node(T data, Node parent) {
            this.data = data;
            this.parent = parent;
        }

        public void setLeft(Node left) {
            this.left = left;
        }

        public void setRight(Node right) {
            this.right = right;
        }
    }
}

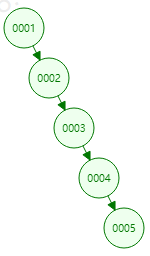
二叉排序树可能会退化程链表