数据结构-优先队列与堆

前言

​ 好吧，我把大部分图片都改成上传图库用地址打开了，这样128M应该还能让我再撑一会，回头如果有钱再买个云服务器吧= =。那么今天就接着来写另一个数据结构--堆qwq

优先队列

​ 优先队列指的是支持每次挑选出优先级最高的元素出队，同时支持元素入队的队列。而这两个操作的实现我们往往使用的是二叉堆。

二叉堆

​ 二叉堆(后面简称堆)是一个完全二叉树(注意与满二叉树区分开)，且满足父节点的值不小于子节点的值。由于是完全二叉树，堆的每个节点可以直接找到自己的父节点(pos>>1)和左右子节点(pos <<1和(pos <<1 )+ 1)，且最底层的叶节点尽量靠左。二叉堆常用操作就是insert插入元素和deleteMin删除最小值

代码测试题目为洛谷模板题，完整代码会另外出博客

insert

​ 现在要将一个元素插入到堆中那么直接将它放到最后一个然后和父节点比较，若新元素优先级大(优先级取决于自己定义)则与父节点互换，直至新元素的位置满足要求。

代码实现:

void insert(int x) {
    hep[++tot]=x; int now=tot; //hep[]存储整个堆 tot为堆当前总元素量
    while((now>>1) && hep[now>>1]>hep[now])
         swap(hep[now>>1],hep[now]),now>>=1;
}

deleteMin

​ 删除最小只需要将hep[1]与hep[tot]交换然后tot--，之后让根不断向下沉(具体来说就是和较小的子节点交换)直至满足堆的形式。

代码实现:

void deleteMin() {
    hep[1]=hep[tot]; tot--;
    for(int now=1,minn;(now<<1)<=tot;now=minn) {
        int ls=now<<1,rs=(now<<1)+1;
        if(hep[ls]<hep[rs]) minn=ls; else minn=rs;
        if(hep[now]>hep[minn]) swap(hep[now],hep[minn]);
    }
}

可并堆

​ 可并堆也是一个抽象数据结构，就是在原来优先队列的基础上增加一个合并merge操作，即将两个可并堆合并为一个。下面说明几种实现可并堆的方法。

左偏树

定义

​ 左偏树的节点在有一个键值的基础上增加了一个距离(dis)值，表示当前节点到它后代中最近的外节点中间的边数，其中外节点指的是左子树或右子树为空的节点。特别的，外节点的dis值为0，空节点的dis值为1，左偏树的距离指的是根节点的dis值。

​ 左偏树是一个二叉树，结构在堆序(满足父节点不大(小)于子节点，但不保证是完全二叉树)的基础上还要求左子节点的dis值不小于右子节点(即左偏性质)。

性质

1. 跟据左偏性质，我们可以发现父节点的dis值为右子节点的dis+1。
2. 若左偏树的距离为定值，节点数最少的左偏树为完全二叉树。节点数最少即当dis[ls[i]]==dis[rs[i]]时，形成结构就是满二叉树。
3. 若左偏树距离为k，节点数最少为 (2^{k+1}-1) 。由2节点数最少时是一个高为k的满二叉树，满二叉树节点数(2^{k+1}-1)。
4. 节点为n的左偏树距离最大为 $ leftlfloorlog(n+1) ight floor-1$ 。其实就是由3推出。

基本操作

代码测试题目为洛谷模板题 ，完整代码会另外出博客

merge

​ 现在有两个左偏树A、B要合并。首先比较A和B的大小，选择优先值高的作为新树的根(假设为A)，A左子树不动，B去尝试和A的右子树合并，过程与之前相同。

代码细节:

int nd[N][2],fa[N]; //nd[]记录子节点 fa[]并查集
#define ls nd[x][0]
#define rs nd[x][1]
int merge(int x,int y) {
    if(!x||!y) return x+y;
    if(val[x]>val[y]) swap(x,y);
    if(val[x]==val[y]&&x>y) swap(x,y);//题目要求：最小值相同时优先删除编号最小的，一般可不写
    fa[rs=merge(rs,y)]=x;
    if(dis[ls]<dis[rs]) swap(ls,rs);
    dis[x]=dis[rs]+1;
    return x;
}

getro

​ 查找该元素所在堆的根，使用路径压缩并查集

int getro(int x) {return fa[x]=fa[x]==x?x:getro(fa[x]);} 

deleteMin

​ 删除该元素所在堆顶并输出其值

bool deld[N];//记录是否删除，真为已删除
x=getro(x); cout<<val[x]<<endl;
deld[x]=1; //简单的删除操作
fa[x]=fa[ls]=fa[rs]=merge(ls,rs);
//由于使用了路径压缩，有很多点fa[]值为x，需要fa[x]=新根，同时ls和rs也需要防止循环:fa[x]=ls,fa[ls]=x

斜堆

​ 斜堆和左偏树非常像，只是不记录dis值，merge时上面第九行改为不判断直接swap。这样降低了存储空间，达到了平摊意义上的左偏性，但由于不是严格的左偏，右子树可能长度为n= =，使用递归写法可能会爆栈，所以尽量写非递归写法。(代码不写了跟据上面的改改就行)

随机堆

​ 随机堆和斜堆很像= =，就是merge时第九行改为随机swap，比如: if(rand()%2) swap(ls,rs); 坏处和斜堆类似(不靠谱的堆增加了~qwq)

斐波那契堆

​ 这个是(理论上)真正的好东西~，不过实际运用很少，难写且常数很大，不过理论复杂度更低

定义

​ 斐波那契堆是一系列具有堆序(上面有提)的有根树的集合。下面这张图展示了该堆的结构

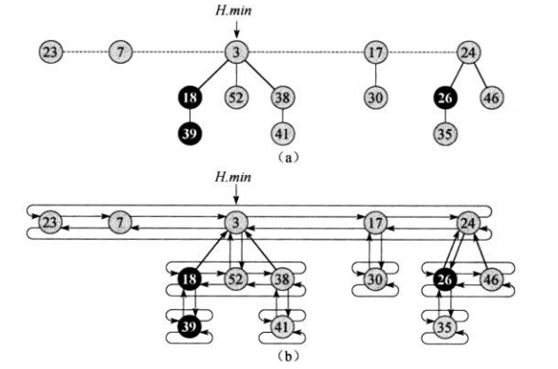
​ b图中展示了具体各个节点保存的指针，可见一个节点u有指向一个父节点的指针fa，一个指向某一个子节点的指针son。而且u的所有孩子连接成一个环形双向链表称为u的孩子链表，环形链表中节点都有left指针和right指针指向左右兄弟。特别的，若孩子链表中只有一个节点，那么它的左右指针都指向自己。另外degree表示u的孩子数目。所有树的根节点也用环形链表连接叫做根链表。

​ 另外斐波那契堆本身需要存min指针指向具有最小键值的树的根节点(称作该堆的最小节点)，如果有多个最小键值，其中一个随机为最小节点。此外就是堆保存堆的节点数n。

​ emm具体的算法过程还是查算法导论吧，里面讲的很清楚了qwq(真的超清楚了，慢慢看就好)，测试题目还是之前的洛谷可并堆模板题，完整代码会另外出博客

​ 这里我没有用指针写，就是用的数组，可能还有其他原因导致最后常数特别大，测试下来还没有左偏树快，但这个理论复杂度要更低一些，另外我删除任意一点的函数也没写，有点写不动了先留坑吧Orz。

int fdeg[N],fa[N]; //fdeg记录度数为i的节点 fa是并查集用的数组
bool vis[N];//记录该节点是否走过
struct Node{
    int key,degree,fa,son,left,right;//key为键值
    bool deld;//是否被删除(该题特有)
}nd[N];
struct Heap{
    int min,n;
}hep[N];

insert

void insrt(int now,int u) { //将一个节点插入一个堆的根链表中
    Node &x=nd[u]; Heap &h=hep[now];
    x.fa=0;
    if(!h.min) {
        x.left=x.right=u;
        h.min=u;
    } else {
        Node &y=nd[h.min],&z=nd[y.right];
        x.left=z.left; x.right=y.right;
        y.right=z.left=u;
        if(y.key>x.key||(y.key==x.key&&h.min>u)) h.min=u;
        // ||之后的部分为该题特有
    }
    h.n++;
}

merge

Heap merge(int u,int v) { //合并两个堆
    Heap &h1=hep[u],&h2=hep[v],h;
    Node &a1=nd[h1.min],&b1=nd[a1.right];
    Node &a2=nd[h2.min],&b2=nd[a2.left];
    b1.left=a2.left,b2.right=a1.right;
    a1.right=h2.min,a2.left=h1.min;
    h.min=h1.min;
    if(!h1.min || (h2.min&&a2.key<a1.key)) h.min=h2.min;
    h.n=h1.n+h2.n;
    return h;
}

link

void link(int now,int u,int v) { //将v变成u的子节点 为consoldate辅助
    Node &x=nd[u],&y=nd[v];
    nd[y.left].right=y.right;
    nd[y.right].left=y.left;
    if(x.son) {
        Node &a=nd[x.son],&b=nd[a.right];
        y.left=x.son,y.right=a.right;
        a.right=v,b.left=v;
    } else {
        x.son=v;
        y.left=y.right=v;
    }
    y.fa=u; x.degree++;
}

consoldate

void consoldate(int now) { //将删除后的堆进行整理合并，防止堆变成链表 为deleteMin的后续工作
    Ms(fdeg,0);Ms(vis,0);
    Heap &h=hep[now];
    int cur=h.min;
    while(!vis[cur]) {
        int d=nd[cur].degree,nxt=nd[cur].right; vis[cur]=1;
        while(fdeg[d]) {
            Node &y=nd[fdeg[d]],&x=nd[cur];
            if(x.key>y.key||(x.key==y.key&&cur>fdeg[d])) swap(cur,fdeg[d]);
            // ||后为该题特殊要求
            link(now,cur,fdeg[d]);
            fdeg[d]=0; d++;
        }
        fdeg[d]=cur;
        cur=nxt; 
    }
    h.min=0;
    Fo(i,0,ceil(log2((double)h.n))+1) if(fdeg[i]) {
        int u=fdeg[i]; Node &x=nd[u];
        insrt(now,u); h.n--;
    }
}

deleteMin

int deleteMin(int now) { //删除并返回最小值，同时对剩下的进行合并(consoldate)
    Heap &h=hep[now];
    Node &x=nd[h.min];
    if(!h.min) return 0;
    int cur=x.son;
    Fo(i,1,x.degree) {
        int nxt=nd[cur].left;
        insrt(now,cur); h.n--;
        nd[cur].fa=0;
        cur=nxt;
    }
    nd[x.left].right=x.right;
    nd[x.right].left=x.left;
    x.deld=1; x.son=0;
    if(x.right==h.min) h.min=0;
    else { 
        h.min=x.right;
        consoldate(now);
    }
    h.n--;
    return x.key;
}

配对堆

​ 暂时留坑吧，整完斐波那契堆以后有点精神疲劳了= =