WYT的刷子
WYT有一把巨大的刷子,刷子的宽度为M米,现在WYT要使用这把大刷子去粉刷有N列的栅栏(每列宽度都为1米;每列的高度单位也为米,由输入数据给出)。
使用刷子的规则是:
1.与地面垂直,从栅栏的底部向上刷
2.每次刷的宽度为M米(当剩余栅栏宽度不够M米的话,刷子也可以使用,具体看样例2)
3.对于连续的M列栅栏,刷子从底向上,刷到的高度只能到这M列栅栏的最低高度。
WYT请你回答两个问题:
1、最少有多少个单位面积不能刷到(单位面积为1平米)
2、在满足第一问的条件下,最少刷几次?
输入
共两行:
第一行两个整数N和M。
第二行共N个整数,表示N列栅栏的高度
输出
一行,两个整数,分别为最少剩余的单位面积数量和最少刷的次数。
Input1:
5 3
5 3 4 4 5
Output1:
3
2
Input2:
10 3
3 3 3 3 3 3 3 3 3 3
Output2:
0
4
Input3:
7 4
1 2 3 4 3
Output3:
4
4
样例1的解释:
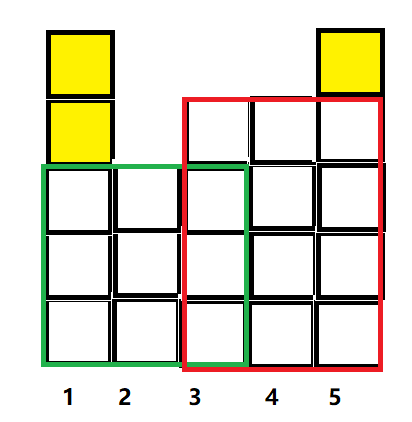
高度分别为 5 3 4 4 5
如上:
黄色的方块表示共有3个单位面积没刷上
绿色的框和红色的框表示一共刷了两次。
数据范围:
30%的数据:N<=10^3
50%的数据:N<=10^5
100%的数据:1<=N<=10^6, 1<=M<=10^6,N>=M, 每列栅栏的高度<=10^6.
思路:
单调栈裸题
利用和求最大子矩形一样的方法,我们可以用单调栈求出每个高度它对应的区间
如果这个区间小于m,则显然刷不到这个点的最高处
然后我们O(N)的扫三遍
第一遍判出哪些地方一定到不了最高点
第二遍和第三遍求出这些到达不了最高点的地方能达到多高
然后再O(n)扫一遍
就能得到有多少个涂不了色的了
至于涂得次数,贪心就好了
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define rii register int i #define rij register int j using namespace std; int n,m,zl[1000005],r[1000005],l[1000005]; long long sum; int sta[1000005],top,sj[1000005],bj[1000005]; inline int rd(){ register int x=0,f=1;char ch=getchar(); while(!isdigit(ch)) {f=ch=='-'?0:1;ch=getchar();} while(isdigit(ch)) {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();} return f?x:-x; } int main() { freopen("wyt.in","r",stdin); freopen("wyt.out","w",stdout); n=rd(),m=rd(); for(rii=1;i<=n;i++) { zl[i]=rd(); sum+=zl[i]; } for(rii=1;i<=n;i++) { if(top==0) { top++; sta[top]=i; continue; } while(zl[sta[top]]>zl[i]) { r[sta[top]]=i-1; top--; } top++; sta[top]=i; } while(top!=0) { r[sta[top]]=n; top--; } for(rii=n;i>=1;i--) { if(top==0) { top++; sta[top]=i; continue; } while(zl[sta[top]]>zl[i]) { l[sta[top]]=i+1; top--; } top++; sta[top]=i; } while(top!=0) { l[sta[top]]=1; top--; } for(rii=1;i<=n;i++) { if(r[i]-l[i]+1<m) { bj[i]=1; } } for(rii=1;i<=n;i++) { if(bj[i]==1) { sj[i]=sj[i-1]; } else { sj[i]=zl[i]; } } for(rii=n;i>=1;i--) { if(bj[i]==1) { sj[i]=max(sj[i+1],sj[i]); } } for(rii=1;i<=n;i++) { sum-=sj[i]; } cout<<sum<<endl; int ans=0; int val=sj[1],l=1; for(rii=2;i<=n;i++) { if(sj[i]!=val) { int sl=(i-l)/m; if(sl*m<(i-l)) { sl++; } ans+=sl; l=i; val=sj[i]; } } int sl=(n-l+1)/m; if(sl*m<(n-l+1)) { sl++; } ans+=sl; cout<<ans; return 0; }