T1:
Black Rock Shooter
1.题目大意:
在人气动漫Black Rock shooter 中,当加贺里对麻陶 说出了“滚回去“以后,与此同时,在另一个心灵世界里,BRS 也遭到了敌人的攻击。此时,一共有n 个攻击排成一行朝着她飞了过来,每个攻击有一个伤害值。并且每个攻击伤害可能随时变化。BRS的攻击可以打掉一段连续的攻击。现在,给出m段攻击,求出BRS最多可以打掉此段里多少的伤害(就是说从给定一段里选择连续一段打掉)。伤害从1到n编号。
2.输入格式:
第一行2个整数:n,m第二行n个数:第i个数代表第i个攻击第3到2+m行:每行三个数k,x,y。若k=1,x,y代表查询的区间。若k=2,代表第x个攻击伤害改为了y所有的伤害值绝对值<=1000
3.输出格式:
对于每次k=1,输出一个整数代表最大值
4.数据范围:
对于20%的数据:n,m<=100
对于60%的数据:n,m<=3000
对于100%的数据:n<=500000,m<=100000
思路:
这道题我不多说了,出门左转GSS3不谢
T2:
Fy's dota2
1.题目大意
Fy觉得自己玩cf,lol这种高端游戏已经够厉害了,于是他决定去玩dota2.
结果fy的鼠标右键坏了,所以他就等到2250买了把闪烁匕首,用跳刀前进,准备去送泉水。
但是fy一次最多前进k的距离,泉水离fy现在的距离是n。
Fy想知道他到泉水的方案数。
2.输入格式:
第一行2个整数:k,n
3.输出格式:
一行1个整数:代表答案对7777777取膜的结果
思路:
这道题其实首先我们可以写出一个暴力DP方程
for(rii=0;i<=n-1;i++) { for(rij=1;j<=k;j++) { if(j+i<=n) { dp[j+i]+=dp[i]; } } }
但O(n*k)的复杂度难以接受
怎么办?
我们知道,斐波那契数列是可以用矩阵快速幂优化的
其递推公式为F[i]=F[i-1]+F[I-2]
那我们对符合该式模式的其他递推式也进行优化即可
T3:
Olddriver’s books
1.题目大意:
Olddriver的书多的吓人,什么算法导论,组合数学英文版(orz)。。。。。。
他把n本书都放在身后的桌子上,每本书有一定的面积,并且书可以覆盖,求n本书覆盖桌面的面积
2.输入格式:
输入第一行为一个数N,表示书的数量。
下面N行,每行四个整数,分别表示每个书的左下角和右上角的坐标。
3.输出格式:
输出只有一行,一个整数,表示图形的面积。
思路:
正解离散化扫描线,不多说了
这里我想讲一下后来我发现的另一种算法:合并正方形
如果两个正方形不相交,我们直接跳过
但如果相交呢?
我们来看图:
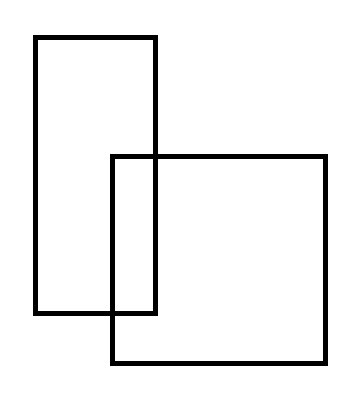
我们可以将这个矩形变成一个大矩形
重复的减去,新加入部分也减去
(减去的是图中蓝色部分)

这样我们就得到了一个新的矩形
用这个新的矩形继续匹配
最坏情况复杂度为O(n^3)
嗯,n才100
过了