POJ 2559 Largest Rectangle in a Histogram

这是单调栈的模版题。
首先，最优解的矩形的高一定等于某个单位直方图的高（可用反证法证明）。
接着，我们可以发现最优解一定是有某个单位直方图向左右尽可能拓展所得到的矩形。
然后，我们引入单调栈。如果有一系列高度非下降的直方图突然高度下降，如图，则分别以高于新直方图的高度构建矩形，求面积。

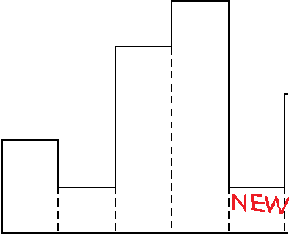
求矩形宽度时，我们可以新直方图的坐标减去矩形直方图的最左坐标。

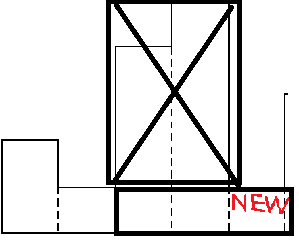
删除完栈中比new高的直方图后，图中画叉的区域是不可用的，所以new可以拓展长度到最后删的直方图的最左端。
最后，方便起见，我们应该在n+1的位置加入一个高度为0的直方图。
代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e5+10;
int a[N],n,sta[N],top;
ll ans;
#define g getchar()
void qr(int &x)
{
	char c=g;x=0;
	while(!('0'<=c&&c<='9'))c=g;
	while('0'<=c&&c<='9')x=x*10+c-'0',c=g;
}
void write(ll x)
{
	if(x/10)write(x/10);
	putchar(x%10+'0');
}
int main()
{
	a[0]=0;
	while(qr(n),n)
	{
		for(int i=1;i<=n;i++)qr(a[i]);
		top=a[++n]=ans=0;
		for(int i=1;i<=n;i++)
		{
			if(a[i]>=a[sta[top]])sta[++top]=i;
			else
			{
				while(top>0&&a[sta[top]]>a[i])
				{
					ans=max(ans,(ll)(i-sta[top])*a[sta[top]]);
					--top;
				}
				a[sta[++top]]=a[i];
			}
		}
		write(ans);puts("");
	}
	return 0;
}