Caioj 1918 & CH 0x20搜索（0x28IDA*）例题3：Square Destroyer

【题意】
下图左侧显示了一个用24根火柴棍构成的完整3×3网格。
所有火柴的长度都是1。
您可以在网格中找到许多不同大小的正方形。
在左图所示的网格中，有9个边长为1的正方形，4个边长为2的正方形和1个边长为3的正方形。
组成完整网格的每一根火柴都有唯一编号，该编号从上到下，从左到右，从1开始按顺序分配。
如果你将一些火柴棍从完整网格中取出，形成一个不完整的网格，则一部分正方形将被破坏。
右图为移除编号12,17和23的三个火柴棍后的不完整的3×3网格。
这次移除破坏了5个边长为1的正方形，3个边长为2的正方形和1个边长为3的正方形。
此时，网格不具有边长为3的正方形，但仍然具有4个边长为1的正方形和1个边长为2的正方形。

现在给定一个（完整或不完整）的n×n（n不大于5）网格，求至少再去掉多少跟火柴棒，可以使得网格内不再含有任何尺寸的正方形。

【输入格式】
输入包含T组测试用例。
测试用例的数量T在输入文件的第一行中给出。
每个测试用例由两行组成：
第一行包含一个整数n，表示网格的规模大小。
第二行以非负整数k开头，表示所给网格相较完整的n×n网格所缺少的火柴杆数量，后跟k个整数表示所有缺少的火柴杆的具体编号。
注意，如果k等于零，则表示输入网格是完整的n×n网格。

【输出格式】
每个测试用例输出一个结果，表示破坏所有正方形，所需的去掉火柴棒的最小数量。
每个结果占一行。

【输入样例】
2
2
0
3
3 12 17 23
【输出样例】
3
3

这是一道非常繁琐的题目。难点是火柴的编号处理和图形的处理。
为了方便，我们用两种坐标(x,y)定位每根火柴的位置。
如图是3*3的网格的火柴的x坐标。

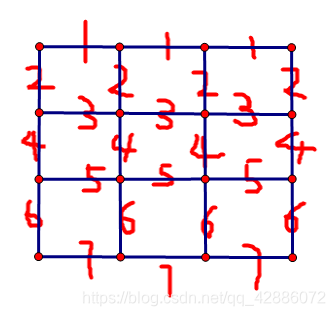
可以发现，x坐标为奇数则火柴为横的，否则为竖的。
类似的，y坐标如下。

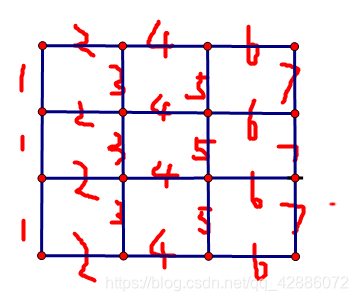
可以发现，y坐标为偶数则火柴为横的，否则为竖的。

//朴素版编号
s=2*n+1;tot=0;
for(int i=1;i<=s;i++)
    for(int j=1;j<=s;j++)
        if((i&1)!=(j&1))id[i][j]=++tot;//一根火柴的x，y坐标的奇偶性必然不同
//不用判断的方法
s=2*n+1;tot=0;
for(int i=1;i<=s;i++) 
	for(int j=-(!(i&1))+2;j<=s;j+=2)
		id[i][j]=++tot;

接下来，我们定义两个二维数组（vector实现）e，g，分别表示火柴所属的正方形的编号，正方形所围成的火柴的编号。

给正方形编号
正方形边的坐标。

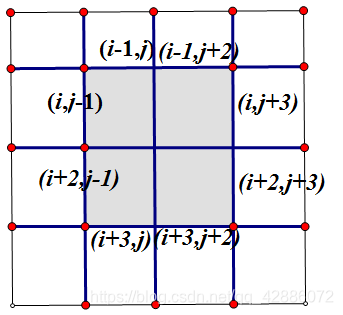
可以发现，如果我们先枚举$i,j,len(边长)$.
那么左边的边的编号的横坐标每次增加2.
右边的边的编号的纵坐标比对应位置多$2*len-1$
上边的边的编号的纵坐标每次增加2.
下面的边的编号的横坐标比对应位置多$2*len-1$

为了使正方形大小单调递增。
我们先枚举$a$,表示$2*len-1$.（即正方形的规模）
再枚举两个偶数$i,j$.
最后枚举$[0,a)$的偶数即可。

	tot=0;
	for(int a=1;a<s;a+=2)//规模——a/2是边长。 
		for(int i=2;i+a<=s;i+=2)//竖边 
			for(int j=2;j+a<=s;j+=2) {//横边
				++tot;
				for(int x=0;x<a;x+=2) {
					e[id[x+i][j-1]].push_back(tot);//left 
					e[id[x+i][j+a]].push_back(tot);//right
					e[id[i-1][x+j]].push_back(tot);//up
					e[id[i+a][x+j]].push_back(tot);//down
					g[tot].push_back(id[x+i][j-1]);
					g[tot].push_back(id[x+i][j+a]);
					g[tot].push_back(id[i-1][x+j]);
					g[tot].push_back(id[i+a][x+j]);
				}
			}

以上我们讲完了最难理解的编号问题。
最后，dfs即可。dfs框架为：每次找出最小的正方形，并对其一条边进行删除。
再辅以估价函数，可以跑得更快。

代码：

#include<cstdio>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=65;
int n,k,s,tot,tmp,id[13][13],dep;
vector<int>e[N],g[N],empty;
bool v[N];
int gj() {
	bool w[N];memcpy(w,v,sizeof w);
	int ans=0;
	for(int i=1;i<=tot;i++) {//把每个正方形的所有边都删除，单只算删除一次。 
		if(w[i]) {
			if(!ans)tmp=i;//最小正方形。
			++ans;
			for(int j=0;j<g[i].size();j++)//枚举出每一条边 
				for(int x=0;x<e[g[i][j]].size();x++)//把边对应的正方形删掉。 
					w[e[g[i][j]][x]]=0;
		}
	}
	return ans;
}
bool dfs(int now) {
	int cnt=gj();
	if(!cnt)return 1;
	if(now+cnt>dep)return 0;
	bool w[N];memcpy(w,v,sizeof w);
	int tmp0=tmp;
	for(int i=0;i<g[tmp0].size();i++) {//枚举最小正方形的边 
		int st=g[tmp0][i];
		for(int j=0;j<e[st].size();j++)//删除边——这些正方形都不可以用了 
			v[e[st][j]]=0;
		if(dfs(now+1))return 1;
		memcpy(v,w,sizeof v);
	}
	return 0;
}
void solve() {
	scanf("%d%d",&n,&k);
	s=2*n+1;tot=0;
	for(int i=1;i<=s;i++) 
		for(int j=-(!(i&1))+2;j<=s;j+=2)
			id[i][j]=++tot;
	for(int i=1;i<=tot;i++)e[i]=empty;
	tot=n*(n+1)*s/6;
	for(int i=1;i<=tot;i++)g[i]=empty;
	tot=0;
	for(int a=1;a<s;a+=2)//规模——a/2是边长。 
		for(int i=2;i+a<=s;i+=2)//竖边 
			for(int j=2;j+a<=s;j+=2) {//横边
				++tot;
				for(int x=0;x<a;x+=2) {
					e[id[x+i][j-1]].push_back(tot);//left 
					e[id[x+i][j+a]].push_back(tot);//right
					e[id[i-1][x+j]].push_back(tot);//up
					e[id[i+a][x+j]].push_back(tot);//down
					g[tot].push_back(id[x+i][j-1]);
					g[tot].push_back(id[x+i][j+a]);
					g[tot].push_back(id[i-1][x+j]);
					g[tot].push_back(id[i+a][x+j]);
				}
			}
	memset(v,1,sizeof v);
	while(k--) {
		int a;scanf("%d",&a);
		for(int i=0;i<e[a].size();i++)
			v[e[a][i]]=0;
	}
	dep=0;
	while(!dfs(0))dep++;
	printf("%d
",dep);
}
int main() {
	int T;scanf("%d",&T);
	while(T--)solve();
	return 0;
}