POJ 1733 Parity game

前言

并查集是一种维护可传递关系的有力数据结构！

---

分析

值域那么大，所以明显要用离散化。

设$sum$数组表示前缀1出现的次数。对于每个回答有两种情况：

1. $s[lsim r]$有偶数个1，则$2|sum[r]-sum[l-1]$,$sum[l-1],sum[r]$奇偶性相同。
2. $s[lsim r]$有奇数个1，则$2|sum[r]-sum[l-1]+1$,$sum[l-1],sum[r]$奇偶性不同。

因为奇偶性关系具有如下传递性：

1. $x、y$奇偶性相同，$y、z$奇偶性相同，则$x、z$奇偶性相同。
2. $x、y$奇偶性相同，$y、z$奇偶性不同，则$x、z$奇偶性不同。
3. $x、y$奇偶性不同，$y、z$奇偶性不同，则$x、z$奇偶性相同。

方法1：

这样我们就可以边带权——用1表示两个变量不同，用0表示两个变量相同。
定义$d[x]$表示x与并查集中父亲的奇偶性关系，就可以很轻松地跑了。

连接两个集合时，需要注意的是边权的长度。
设$ans$表示两个变量的奇偶性相同（1表示不同，0表示相同）,$x,y$表示$l-1,r$的离散值,$p,q$为$x,y$的祖先(并查集代表)。
则$ans=dis[xsim p] operatorname{xor}dis[psim q]operatorname{xor} dis[qsim y](这里的dis是不同与d的)$
所以，若把$p连向q$，则$d[p]=d[x]operatorname{xor} d[y]operatorname{xor} ans$.

代码：

#include<cstdio>
#include<cctype>
#include<cstring>
#include<algorithm>
#define g getchar()
using namespace std;
typedef long long ll;
const int N=20010;
template<class o>void qr(o&x) {
	char c=g;x=0;int f=1;
	while(!isdigit(c)){if(c=='-')f=-1;c=g;}
	while(isdigit(c))x=x*10+c-'0',c=g;
	x*=f;
}
void write(int x) {
	if(x/10)write(x/10);
	putchar(x%10+'0');
}

int n,m,d[N],fa[N];
int findfa(int x) {
	if(fa[x]==x)return x;
	int root=findfa(fa[x]);
	d[x]^=d[fa[x]];
	return fa[x]=root;
}
struct rec {int l,r;bool ans;}q[N>>1];
int a[N],tot;
void disc() {
	qr(n);qr(m);tot=0;
	for(int i=1;i<=m;i++) {
		qr(q[i].l),qr(q[i].r);
		char s[7];scanf("%s",s);
		q[i].ans=(s[0]=='o');
		a[++tot]=q[i].l-1;a[++tot]=q[i].r;
	}
	sort(a+1,a+tot+1);
	tot=unique(a+1,a+tot+1)-(a+1);
}
int main() {
	disc();for(int i=1;i<=tot;i++)fa[i]=i;
	for(int i=1;i<=m;i++) {
		int x=lower_bound(a+1,a+tot+1,q[i].l-1)-a,
			y=lower_bound(a+1,a+tot+1,q[i].r)-a,
			ans=q[i].ans,tx,ty;
		tx=findfa(x);ty=findfa(y);
		if( tx == ty ) {
			if( (d[x]^d[y]) != q[i].ans )
				{write(i-1);puts("");return 0;}
		}
		else {
			fa[ty]=tx;
			d[ty]=d[x]^d[y]^ans;
		}
	}
	write(m);puts("");
	return 0;
}

总结：

边带权并查集其实就是用并查集记录无向图的边。

---

方法2：

我们把每个变量$(sum[x])$拆成两个点——x_odd,x_even（分别表示$sum[x]$为奇数的情况和$sum[x]$为偶数的情况.)
本质上是把点分成两个集合。
设$x,y$为$l-1,r$的离散值.那么对于每个回答，分两种情况讨论：

1. 奇偶性相同。若x_odd与y_even在同一个集合内，则矛盾。
   否则，连接(x_odd,y_odd),(x_even,y_even).

2. 奇偶性不同。若x_odd与y_odd在同一个集合内，则矛盾。
   否则，连接(x_odd,y_even),(x_even,y_odd).

并查集维护的实际上是这样对称的关系。

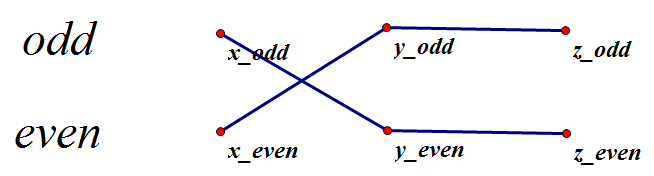
这是一种更加直观的做法。

代码:

//扩展域——其实就是把一个点拆分成几个点。 
#include<cstdio>
#include<cctype>
#include<cstring>
#include<algorithm>
#define g getchar()
using namespace std;
typedef long long ll;
const int N=20010;
template<class o>void qr(o&x) {
	char c=g;x=0;int f=1;
	while(!isdigit(c)){if(c=='-')f=-1;c=g;}
	while(isdigit(c))x=x*10+c-'0',c=g;
	x*=f;
}
void write(int x) {
	if(x/10)write(x/10);
	putchar(x%10+'0');
}

int fa[N],m;
int findfa(int x) { return fa[x] == x?x:fa[x] = findfa(fa[x]);}
struct node {int x,y;bool ans;}q[N>>1];
int a[N],tot;
void disc() {
	qr(m);qr(m);tot=0;char s[8];
	for(int i=1;i<=m;i++) {
		qr(q[i].x);qr(q[i].y);
		scanf("%s",s);
		q[i].ans = (s[0] == 'o');
		a[++tot]=q[i].x-1;
		a[++tot]=q[i].y;
	}
	sort(a+1,a+tot+1);
	tot=unique(a+1,a+tot+1)-(a+1);
}
int main() {
	disc();for(int i=1;i<=2*tot;i++)fa[i]=i;
	for(int i=1;i<=m;i++) {
		int x=lower_bound(a+1,a+tot+1,q[i].x-1)-a;
		int y=lower_bound(a+1,a+tot+1,q[i].y  )-a;
		int x_odd = x,x_even = x + tot;
		int y_odd = y,y_even = y + tot;
		if(!q[i].ans) {
			if(findfa(x_odd)==findfa(y_even)) {
				write(i-1);puts("");
				return 0;
			}
			fa[findfa(x_odd)]=findfa(y_odd);
			fa[findfa(x_even)]=findfa(y_even);
		}
		else {
			if(findfa(x_odd)==findfa(y_odd)) {
				write(i-1);puts("");
				return 0;
			}
			fa[findfa(x_odd)]=findfa(y_even);
			fa[findfa(y_odd)]=findfa(x_even);
		}
	}
	write(m);puts("");
	return 0;
}