描述
小Hi和小Ho破解了一道又一道难题,终于来到了最后一关。只要打开眼前的宝箱就可以通关这个游戏了。
宝箱被一种奇怪的机关锁住:
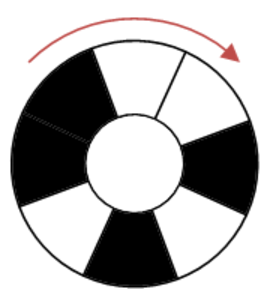
这个机关是一个圆环,一共有2^N个区域,每个区域都可以改变颜色,在黑白两种颜色之间切换。
小Ho控制主角在周围探索了一下,果然又发现了一个纸片:
机关黑色的部分表示为1,白色的部分表示为0,逆时针连续N个区域表示一个二进制数。打开机关的条件是合理调整圆环黑白两种颜色的分布,使得机关能够表示0~2^N-1所有的数字。
我尝试了很多次,终究没有办法打开,只得在此写下机关破解之法。
——By 无名的冒险者
小Ho:这什么意思啊?
小Hi:我给你举个例子,假如N=3,我们通过顺时针转动,可以使得正下方的3个区域表示为:
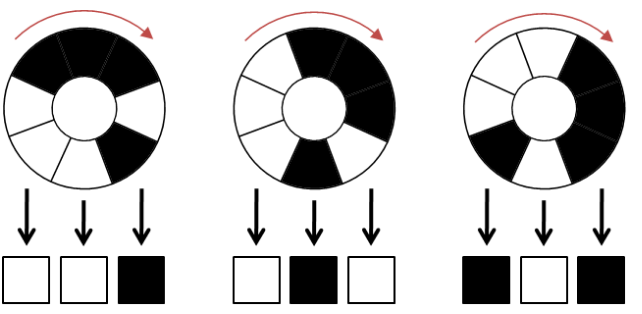
因为黑色表示为1,白色表示为0。则上面三个状态分别对应了二进制(001),(010),(101)
每转动一个区域,可以得到一个新的数字。一共可以转动2N次,也就是2N个数字。我们要调整黑白区域的位置,使得这2N个数字恰好是0~2N-1
小Ho:我懂了。若N=2,则将环上的黑白色块调整为"黑黑白白",对应了"1100"。依次是"11","10","00","01"四个数字,正好是0~3。那么这个"黑黑白白"就可以打开机关了咯?
小Hi:我想应该是的。
小Ho:好像不是很难的样子,我来试试!
输入
第1行:1个正整数,N。1≤N≤15
输出
第1行:1个长度为2^N的01串,表示一种符合要求的分布方案
样例输入
3
样例输出
00010111
题解
可以把每k位二进制数看作一个点,它与左移一位+0和+1形成的新k位二进制数存在一条边相连。
这样只要每次不走重边,每次形成的都是一个新的数,这样走1<<n次,就可以生成0到1<<n -1的所有数字了
#include <bits/stdc++.h>
#define ll long long
#define inf 1000000000
#define PI acos(-1)
#define bug puts("here")
#define REP(i,x,n) for(int i=x;i<=n;i++)
#define DEP(i,n,x) for(int i=n;i>=x;i--)
#define mem(a,x) memset(a,x,sizeof(a))
using namespace std;
inline int read(){
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-') f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
const int N=(1<<15)+1;
bool vis[N];
int ans[N],tn,n;
bool euler(int u,int step){
if(vis[u]) return false;
if(step==tn+1) return true;
ans[step]=u&1;
vis[u]=true;
if(euler((u<<1)&tn,step+1)) return true;
if(euler((u<<1|1)&tn,step+1)) return true;
vis[u]=false;
return false;
}
int main(){
n=read();
tn=(1<<n)-1;
euler(0,1);
for(int i=1;i<n;i++)
printf("0");
for(int i=1;i<=tn-n+2;i++)
printf("%d",ans[i]);
return 0;
}