(1)归并排序(经典)
(2)冒泡法
(3)快速排序
(4)插入排序
(5)希尔(shell)排序
(6)选择排序
(7)堆排序
附:
排序算法原理:http://zh.wikipedia.org/wiki/Category:%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95
flash演示:http://www.tyut.edu.cn/kecheng1/site01/suanfayanshi/list.asp?id=7
归并排序:(经典例题 网址 )
归并算法基本思路设两个有序的子文件放在同一向量中相邻的位置上:R[low..m],R[m+1..high],先将它们合并到一个局部的暂存向量R1中,待合并完成后将R1复制回R[low..high]中。合并过程中,设置i,j和p三个指针,其初值分别指向这三个记录区的起始位置。合并时依次比较R[i]和R[j]的关键字,取关键字较小的记录复制到R1[p]中,然后将被复制记录的指针i或j加1,以及指向复制位置的指针p加1。重复这一过程直至两个输入的子文件有一个已全部复制完毕(不妨称其为空),此时将另一非空的子文件中剩余记录依次复制到R1中即可。
左边小左边,左边++;右边小取右边,右边++
用比较简单的人话说就是:其实归并排序就是分治思想的一种应用,就是每次用二分的方式,每次将序列分成两部分,然后知道分成每一部分两个数为止,
在这一整块作为一部分,依次从该该整区间的左区间第一个数开始和右边(即从mid右面的)第一个数作比较,将小的放到合并序列中
这样就将该小的范围排好序了。之后一次排序,知道当前区间为整个大区间为止
归并排序是利用递归和分而治之的技术将数据序列划分成为越来越小的半子表,再对半子表排序,最后再用递归步骤将排好序的半子表合并成为越来越大的有序序列,归并排序包括两个步骤,分别为:
1)划分子表
2)合并半子表
首先我们来讨论归并算法,归并算法将一系列数据放到一个向量中,索引范围为[first,last],这个序列由两个排好序的子表构成,以索引终点(mid)为分界线,以下面一个序列为例
7,10,19,25,12,17,21,30,48
这样的一个序列中,分为两个子序列 7,10,19,25 和 12,17,21,30,48,如下图所示:
再使用归并算法的时候的步骤如下:
第一步:比较v[indexA]=7和v[indexB]=12,将较小的v[indexA]取出来放到临时向量tempArray中,然后indexA加1
第二步:比较v[indexA]=10和v[indexB]=12,将较小的10放到临时变量tempArray中,然后indexA++;
第三步:比较v[indexA]=19与v[indexB]=12,将较小的12存放到临时变量tempArray中,然后indexB++;
第四步到第七步:按照以上规则,进行比对和存储,得到如下结果:
最后一步:将子表b中剩余项添加到临时向量tempArray中
然后将临时变量中的值按照索引位置,拷贝回向量v中,就完成了对向量v的归并排序
算法函数为:
public void Merger(int[] v, int first, int mid, int last)
{
Queue<int> tempV = new Queue<int>();
int indexA, indexB;
//设置indexA,并扫描subArray1 [first,mid]
//设置indexB,并扫描subArray2 [mid,last]
indexA = first;
indexB = mid;
//在没有比较完两个子标的情况下,比较 v[indexA]和v[indexB]
//将其中小的放到临时变量tempV中
while (indexA < mid && indexB < last)
{
if (v[indexA] < v[indexB])
{
tempV.Enqueue(v[indexA]);
indexA++;
}
else
{
tempV.Enqueue(v[indexB]);
indexB++;
}
}
//复制没有比较完子表中的元素
while (indexA < mid)
{
tempV.Enqueue(v[indexA]);
indexA++;
}
while (indexB < last)
{
tempV.Enqueue(v[indexB]);
indexB++;
}
int index = 0;
while (tempV.Count > 0)
{
v[first+index] = tempV.Dequeue();
index++;
}
}
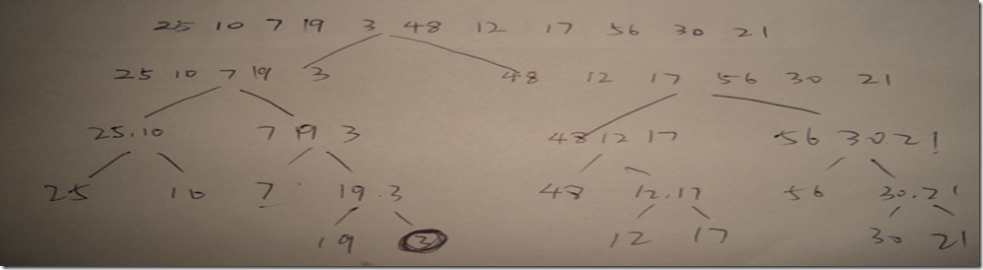
实现归并排序;归并排序算法分为两步,第一步:先将原来的数据表分成排好序的子表,然后调用 Merger 对子表进行归并,使之成为有序表,例如有如下向量:
25,10,7,19,3,48,12,17,56,30,21
对此序列进行归并排序的步骤为:
归并算法函数为
public void MergerSort(int[] v, int first, int last)
{
if (first + 1 < last)
{
int mid = (first + last) / 2;
MergerSort(v, first, mid);
MergerSort(v, mid, last);
Merger(v, first, mid, last);
}
}
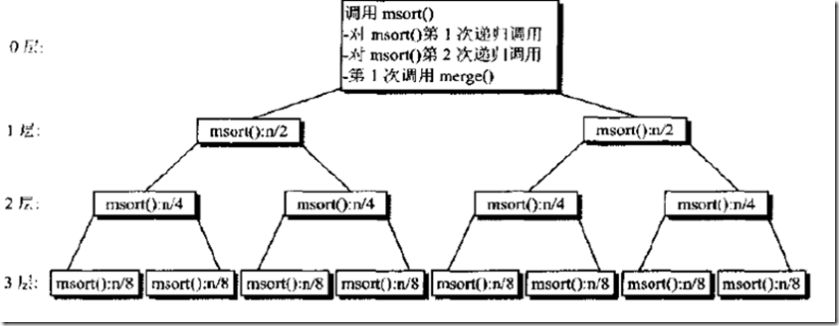
归并算法的划分子表和归并子表与原数据序列次序无关,因此算法的最坏情况,最坏情况和平均情况时间复杂度是一样的
下面是归并算法的函数调用图
template<typename T>
void merge(T array[], int low, int mid, int high)
{
int k;
T *temp = new T[high-low+1]; //申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列
int begin1 = low;
int end1 = mid;
int begin2 = mid + 1;
int end2 = high;
for (k = 0; begin1 <= end1&& begin2 <= end2; ++k) //比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
if(array[begin1]<=array[begin2])
temp[k] = array[begin1++];
else
temp[k] = array[begin2++];
if(begin1 <= end1) //若第一个序列有剩余,直接拷贝出来粘到合并序列尾
memcpy(temp+k, array+begin1, (end1-begin1+1)*sizeof(T));
if(begin2 <= end2) //若第二个序列有剩余,直接拷贝出来粘到合并序列尾
memcpy(temp+k, array+begin2, (end2-begin2+1)*sizeof(T));
memcpy(array+low, temp, (high-low+1)*sizeof(T));//将排序好的序列拷贝回数组中
delete temp;
}
template<typename T>
void merge_sort(T array[], unsigned int first, unsigned int last)
{
int mid = 0;
if(first<last)
{
mid = first/2 +last/2;
merge_sort(array, first, mid);
merge_sort(array, mid+1,last);
merge(array,first,mid,last);
}
}
template<typename T>
void Print(T* r,int n)
{
for (int i=0;i<n;i++)
cout << r[i] << endl;
}
int main()
{
cout << "Welcome..."<< endl;
double r[] ={1.5,3.2,5,6,9.2,7,2,4,8};
QuickSort(r,0,8);
Print(r,9);
return 0;
}
冒泡法: 左右元素相比,往后冒泡
template<typename T>
void BubbleSort(T* r, int n)
{
T temp;
int i,j;
for (i=0;i<n-1;i++)
for (j=0;j<n-i-1;j++)
if (r[j] > r[j+1])
{
temp = r[j];
r[j] = r[j+1];
r[j+1] = temp;
}
}
快速排序 :左边比他小,右边比他大,每次得到一个最左边数据的位置
template<typename T>
void QuickSort(T a[],int low,int high)
{
if(low < high)
{
T elem = a[low];
int l = low, r = high;
while(l < r)
{
while(l < r && a[r] >= elem) r--;
if (l < r)
a[l++] = a[r];
while(l< r && a[l] <= elem) l++;
if (l < r)
a[r--] = a[l];
}
a[r] = elem;
QuickSort(a,low,r-1);
QuickSort(a,r+1,high);
}
}
插入排序:向右移,a[j+1]=a[j]
template<typename T>
void insert_sort(T a[],int n)
{
int i,j;
T elem;
for (i= 1;i<n ;++i)
{
j = i- 1;
elem = a[i];
while(j>=0&& elem < a[j] )
{
a[j+1] = a[j];
j--;
}
a[j+1] = elem;
}
}
/*希尔(shell)排序:把插入排序的改成d即可*/
template<typename T>
void shell_sort(T array[],int len)
{
int inc = len;
do
{
inc = inc/2;
shell_insert(array,inc,len);
}
while (inc >1);
}
选择排序:逐一比较,最小的放前面
template <typename T>
void SelectSort(T a[],int n)
{
int i,j,elemNum;
T elem;
for (i=0;i<n-1;i++)
{
elemNum = i;
for (j= i+1;j<n;j++)
if (a[j] < a[elemNum])
elemNum = j;
if (elemNum != i)
{
elem = a[i];
a[i] = a[elemNum];
a[elemNum] = elem;
}
}
}
堆排序:a[s]>=a[2*s] &&a[s]>=a[2*s+1]
template<typename T>
void Max_heap(T a[],int S,int len)
{
int l = 2*S;
int r = 2*S+1;
int maxI = S;
T elem;
if (l < len && a[l] > a[maxI])
maxI = l;
if (r < len && a[r] > a[maxI])
maxI = r;
if (maxI != S)
{
elem = a[S];
a[S] = a[maxI];
a[maxI] = elem;
Max_heap(a,maxI,len);
}
}
template<typename T>
void HeapSort(T a[],int n)
{
int i;
T elem;
for (i = n/2;i>=0;i--)
Max_heap(a,i,n);
for (i= n-1;i>=1;i--)
{
elem = a[0];
a[0] = a[i];
a[i] = elem;
n = n-1;
Max_heap(a,0,n);
}
}