线段树
- 线段树的每个结点都代表一个区间。
- 线段树有唯一的根节点代表整个范围,比如:[1,N];
- 线段树的每个叶子结点都代表一个长度为1的元区间 [x,x];
- 对于每个内部节点[l,r],它的左节点是[l,m],右节点是[m+1,r],其中m=(l+r)/2(向下取整)
- 图例说明:
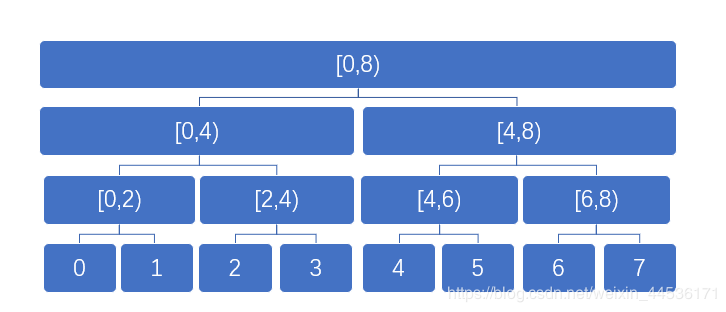
该线段树存储的是[0,7]区间的相应信息。
- 可以得出线段树大约有2n个结点,深度为O(logn)
-
一般采用数组或结构体的方式存储,编号为i的结点的左儿子为2*i,右儿子为2*i+1
- 每个结点维护对应区间的和
- 建树(这里采用了结构体形式)

1 struct SegmentTree 2 { 3 int l, r; 4 int data; 5 } t[N * 4 + 5]; 6 int a[N]; //原始数据数组 7 void build(int p,int l,int r) //存储区间和的线段树 8 { 9 t[p].l = l, t[p].r = r; //节点p代表[l,r] 10 if(l==r) //单点 11 { 12 t[p].data = a[l]; 13 return; 14 } 15 int m = (l + r) / 2; //折半 16 int ls = 2 * p, rs = ls + 1; 17 build(ls, l, m); //建左子树 18 build(rs, m + 1, r); //建右子树 19 t[p].data = t[ls].data + t[rs].data; //p代表的区间和 = ls代表的区间和 + rs代表的区间和 20 }

1 void build(int p,int l,int r) //存储区间最大值的线段树 2 { 3 t[p].l = l, t[p].r = r; 4 if(l==r) 5 { 6 t[p].date = a[l]; 7 return; 8 } 9 int m = (l + r) / 2; 10 int ls = 2 * p, rs = ls + 1; 11 build(ls, l, m); 12 build(rs, m + 1, r); 13 t[p].date = max(t[ls].date,t[rs].date); //p区间的最大值 = max(ls最大值,rs最大值) 14 }
第二段代码需要注意一点:ls和rs为p的两个子区间,故可以通过 t[p].date = max(t[ls].date,t[rs].date);得出p区间的最大值,但是不可以通过ls和p求出rs区间的最大值。
- 修改
参考上图,修改只需要修改对应点以及他的所有祖先即可,复杂度和深度一样为O(logn)

1 void add(int p,int x,int v) //将x位置的数增加v 同样是存储区间和的线段树 2 { 3 if(t[p].l==t[p].r) 4 { 5 t[p].data += v; 6 return; 7 } 8 int m = (t[p].l + t[p].r) / 2; 9 int ls = 2 * p, rs = ls + 1; 10 if(x<=m) 11 add(ls, x, v); 12 else 13 add(rs, x, v); 14 t[p].data = t[ls].data + t[rs].data; 15 }

1 void add(int p,int x,int v) //维护区间最大值的线段树 将x位置的数值改为v 2 { 3 if(t[p].l==t[p].r) 4 { 5 t[p].date = v; 6 return; 7 } 8 int m = (t[p].l + t[p].r) / 2; 9 int ls = 2 * p, rs = ls + 1; 10 if(x<=m) 11 add(ls, x, v); 12 else 13 add(rs, x, v); 14 t[p].date = max(t[ls].date,t[rs].date); 15 }
- 查询
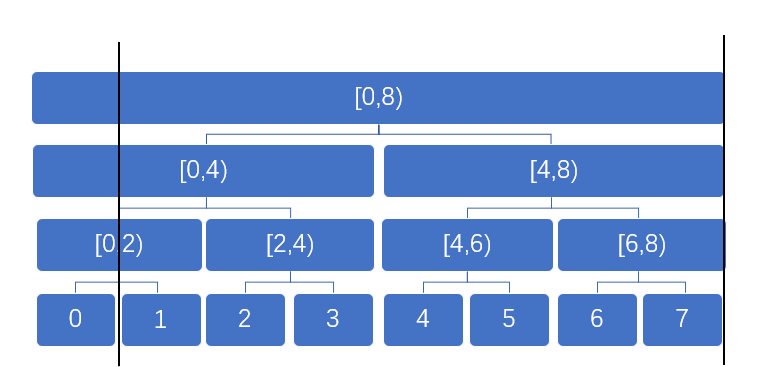
如图:若要查询区间[1,7]的和,则需要把他分成[1,1]、[2,3]、[4,7]三段连续的区间即可
因为查询的是连续的区间所以最多分解为O(logn)个区间

1 int Query(int p,int l,int r) //询问l-r区间和 2 { 3 if(l<=t[p].l&&r>=t[p].r) //l-r完全覆盖了p代表的区间 4 { 5 return t[p].data; //直接返回值 6 } 7 int m = (t[p].l + t[p].r) / 2; //向下取整 8 int ls = 2 * p, rs = ls + 1; 9 int sum = 0; 10 if(l<=m) //p此时的区间的左半边和l-r有交集但不完全被完全覆盖 11 { 12 sum += Query(ls, l, m); //查询左半边 此时的l-r其实是l-m 13 } 14 if(r>m) //这里没有等于 15 { 16 sum += Query(rs, m + 1, r); //同理 17 } 18 }

1 int Query(int p,int l,int r) //询问区间最大值 2 { 3 if(l<=t[p].l&&r>=t[p].r) 4 { 5 return t[p].date; 6 } 7 int m = (t[p].l + t[p].r) / 2; 8 int ls = 2 * p, rs = ls + 1; 9 int maxx=-inf; //初始化最大值为-inf 10 if(l<=m) 11 maxx=max(maxx,Query(ls,l,r)); 12 if(r>m) 13 maxx=max(maxx,Query(rs,l,r)); 14 return maxx; 15 }
以上是线段树的基本操作,数组存储方式的代码实现这里就不贴了,道理相同掌握了一个另一个自然可以写出来。
- Pushdown(延迟标记)
简单来说延迟标记的主要思想就是:如果在执行“区间修改”这个指令时,发现某个区间被修改区间全部覆盖,则以该结点为根的子树的所有结点都应该被修改,若进行逐一更新复杂度会提升,故在回溯之前向该节点p增加一个标记:标识“该节点曾经被修改,但其子节点尚未被更新”。
如果在后续的指令中,需要从结点p向下递归,则再检查p是否具有标记,若有标记,就根据标记信息更新p的两个子结点,同时为p的两个子节点增加标记,然后清除p的标记。
也就是说,除了修改指令中划分的O(logn)个结点之外,对任意结点的修改都延迟到“在后续操作中递归进入他的父节点时”再执行。这些标记被成称为“延迟标记”。
下面是蓝书上Pushdown的模板

1 struct SegmentTree 2 { 3 int l, r; 4 ll sum, add; //add为增量延迟标记 5 #define l(x) t[x].l 6 #define r(x) t[x].r 7 #define sum(x) t[x].sum 8 #define add(x) t[x].add 9 } t[N * 4]; 10 int a[N], n, m; 11 void build(int p,int l,int r) 12 { 13 l(p) = l, r(p) = r; 14 if(l==r) 15 { 16 sum(p) = a[l]; 17 return; 18 } 19 int m = (l + r) / 2; 20 int ls = 2 * p, rs = 2 * p + 1; 21 build(ls, l, m); 22 build(rs, m + 1, r); 23 sum(p) = sum(ls) + sum(rs); 24 } 25 void spread(int p) 26 { 27 if(add(p)) 28 { 29 int ls = 2 * p, rs = 2 * p + 1; 30 sum(ls) += add(p) * (r(ls) - l(ls) + 1); 31 sum(rs) += add(p) * (r(rs) - l(rs) + 1); 32 add(ls) += add(p); 33 add(rs) += add(p); 34 add(p) = 0; 35 } 36 } 37 void change(int p,int l,int r,int d) 38 { 39 if(l<=l(p)&&r>=r(p)) 40 { 41 sum(p) += (ll)d * (r(p) - l(p) + 1); 42 add(p) += d; 43 return; 44 } 45 spread(p); 46 int m = (l(p) + r(p)) / 2; 47 int ls = 2 * p, rs = 2 * p + 1; 48 if(l<=m) 49 change(ls, l, r, d); 50 if(r>m) 51 change(rs, l, r, d); 52 sum(p) = sum(ls) + sum(rs); 53 } 54 ll ask(int p,int l,int r) 55 { 56 if(l<=l(p)&&r>=r(p)) 57 return sum(p); 58 spread(p); 59 int m = (l(p) + r(p)) / 2; 60 int ls = 2 * p, rs = 2 * p + 1; 61 ll val = 0; 62 if(l<=m) 63 val += ask(ls, l, r); 64 if(r>m) 65 val += ask(rs, l, r); 66 return val; 67 }
了解了延迟标记之后则可以用线段树处理区间修改,区间查询的问题
https://www.luogu.org/problemnew/show/P3372
(未完
