已经两个月没有写博客了,今天突然想写了(其实是在补前的)我一直没有看懂treap;现在有点感觉了,就准备写一篇论文,可能有点low;
首先,要知道二叉查找树是啥,这就要请度娘:二叉查找树 百度百科
明白二叉查找树就行;
接着开始骚操作: 平衡树有7大骚操作: 1.treap旋转(zig/zag)操作 2.treap插入操作 3.treap删除操作 4.求一个元素在treap的前驱 5.求一个元素在treap的后继
6.在treap中查找排名第K的元素 7.在treap中求元素的排名
就这样就从第一个开始讲起:
首先我要先然大家看懂我的结构体:
1 struct node{ 2 int l; //左子节点 3 int r; //右子节点 4 int pri; //每个节点的权值 5 int key; //优先级 6 int sze; //以x为根的左子节点的个数 7 int same; //记录重复节点的个数 8 }e[N*2];
1.treap(zig/zag)
首先一棵treap树要保存一个最小堆的性质而这个最小堆性质就有随机生成的key来维护:
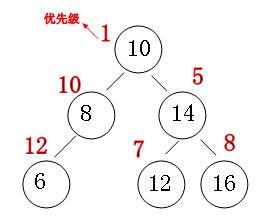 图中的红色部分就是随机生成的key他要符合最小堆的性质,但是插入一个数他可能会不符合最小堆的性质时就要用到左转右转来维护这个最小堆;
图中的红色部分就是随机生成的key他要符合最小堆的性质,但是插入一个数他可能会不符合最小堆的性质时就要用到左转右转来维护这个最小堆;
如: 左图他就破坏了堆的性质就要把它左右旋,图中将12进行右旋得到一个符合条件的树;
左图他就破坏了堆的性质就要把它左右旋,图中将12进行右旋得到一个符合条件的树;
zig:
1 void zig(int &k) //这里必须要加上一个&符号处理父子关系 2 { 3 int y=e[k].l; //选取当前结点的左子节点 4 e[k].l=e[y].r; 5 e[y].r=k; //交换y,k的父子位置,维护BST性质 6 e[y].sze=e[k].sze; //维护子树的size 7 upt(k); //更新节点k的size 8 k=y; 9 } 10 //BST就是二叉搜索树
zag:
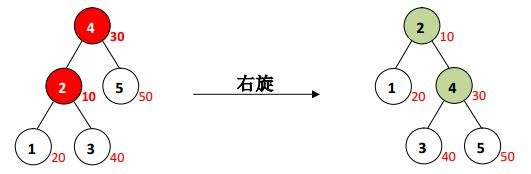 和上面一样操作
和上面一样操作
1 void zag(int &k) 2 { 3 int y=e[k].r; 4 e[k].r=e[y].l; 5 e[y].l=k; 6 e[y].sze=e[k].sze; 7 upt(k); 8 k=y; 9 } 10 和上方的zig的操作一样,就不多说了(就是左改成了右)
2.treap插入操作
给节点随机分配一个优先级,先和二叉排序树的插入一样,先把要插入的点插入到一个叶子上,然后跟维护堆一样,如果当前节点的优先级比根大就旋转,如果当前节点是跟的左儿子就右旋如果当前节点是跟个右儿子就左旋。
代码实现:
1 void Insert(int &k,const int &pre) 2 { 3 if(!k) 4 { 5 k=++pool;e[k].pri=pre;e[k].key=rand(); //rand()是随机函数就是讲树节点的key随机生成 6 e[k].same=e[k].sze=1;e[k].l=e[k].r=0; //新建节点 7 return ; 8 } 9 else ++e[k].sze; 10 if(e[k].pri==pre) ++e[k].same; //重复节点的处理 11 else if(pre<e[k].pri) 12 { 13 Insert(e[k].l,pre); 14 if(e[e[k].l].key<e[k].key) //维护堆的性质 15 zig(k); 16 } 17 else 18 { 19 Insert(e[k].r,pre); 20 if(e[e[k].r].key<e[k].key) //同上 21 zag(k); 22 } 23 return ; 24 }
3.treap删除操作
有了旋转的操作之后,Treap的删除比二叉排序树还要简单。因为Treap满足堆性质,所以我们只需要把要删除的节点旋转到叶节点上,然后直接删除就可以了。具体的方法就是每次找到优先级最大的儿子,向与其相反的方向旋转,直到那个节点被旋转到叶节点,然后直接删除。
代码:
1 void Delete(int &k,const int &pre) 2 { 3 if(e[k].pri==pre) 4 { 5 if(e[k].same>1) 6 { 7 --e[k].same; 8 --e[k].sze; 9 } 10 else if(!e[k].l||!e[k].r) 11 k=e[k].l+e[k].r; 12 else if(e[e[k].l].key<e[e[k].r].key) 13 { 14 zig(k); 15 Delete(k,pre); 16 } 17 else 18 { 19 zag(k); 20 Delete(k,pre); 21 } 22 return ; 23 } 24 --e[k].sze; 25 if(pre<e[k].pri) 26 Delete(e[k].l,pre); 27 else 28 Delete(e[k].r,pre); 29 return ; 30 }
4.求一个元素在treap的前驱
1.从根节点开始访问,初始化最优节点为空节点;
2.如果当前节点的值不大于要求前驱的元素的值,更新最优节点为当前节点,访问当前节点的右子节点;
3.如果当前节点的值大于要求前驱的元素的值,访问当前节点的左子节点;
4.如果当前节点是空节点,查找结束,最优节点就是要求的前驱。
代码:
1 int qianqu(const int &key) 2 { 3 int x=rt,res=-INF; 4 while(x) 5 { 6 if(e[x].pri<key) 7 { 8 res=e[x].pri; 9 x=e[x].r;//要求的前驱为节点x或在节点x的右节点x的右子树内 10 } 11 else 12 x=e[x].l; 13 } 14 return res; 15 }
5.求一个元素在treap的后继
和前驱的基本一样:
1 int houji(const int &key) 2 { 3 int x=rt,res=INF; 4 while(x) 5 { 6 if(e[x].pri>key) 7 { 8 res=e[x].pri; 9 x=e[x].l; 10 } 11 else 12 x=e[x].r; 13 } 14 return res; 15 }
6.在treap中查找排名第K的元素
如果我们想查找第k小的元素或者询问某个元素在Treap中从小到大的排名时,我们就必须知道每个子树中节点的个数。我们称以一个子树的所有节点的权值之和,为子树的大小。由于插入、删除、旋转等操作,会使每个子树的大小改变,所以我们必须对子树的大小进行动态的维护。
对于旋转,我们要在旋转后对子节点和根节点分别重新计算其子树的大小。
对于插入,新建立的节点的子树大小为1。在寻找插入的位置时,每经过一个节点,都要先使以它为根的子树的大小增加1,再递归进入子树查找。
对于删除,在寻找待删除节点,递归返回时要把所有的经过的节点的子树的大小减少1。要注意的是,删除之前一定要保证待删除节点存在于Treap中。
1 int di(int &k) 2 { 3 int x=rt; 4 while(x) 5 { 6 if(e[e[x].l].sze<k&&e[e[x].l].sze+e[x].same>=k) 7 return e[x].pri; 8 if(e[e[x].l].sze>=k) x=e[x].l; 9 else 10 { 11 k-=e[e[x].l].sze+e[x].same; 12 x=e[x].r; 13 } 14 } 15 return 0; 16 }
7.在treap中求元素的排名
1 int piming(const int &key) 2 { 3 int x=rt,res=0; 4 while(x) 5 { 6 if(key==e[x].pri) 7 return res+e[e[x].l].sze+1; 8 if(key<e[x].pri) x=e[x].l; 9 else 10 { 11 res+=e[e[x].l].sze+e[x].same; 12 x=e[x].r; 13 } 14 } 15 return res; 16 }
这个应该是容易操作的;
最后贴一整个代码:
1 #include<bits/stdc++.h> 2 #define INF 0x7fffff 3 #define N 100010 4 using namespace std; 5 struct node{ 6 int l; 7 int r; 8 int pri; 9 int key; 10 int sze; 11 int same; 12 }e[N*2]; 13 int rt,pool,n; 14 void upt(const int &k) 15 { 16 e[k].sze=e[e[k].l].sze+e[e[k].r].sze+e[k].same; 17 } 18 void zig(int &k) 19 { 20 int y=e[k].l; 21 e[k].l=e[y].r; 22 e[y].r=k; 23 e[y].sze=e[k].sze; 24 upt(k); 25 k=y; 26 } 27 void zag(int &k) 28 { 29 int y=e[k].r; 30 e[k].r=e[y].l; 31 e[y].l=k; 32 e[y].sze=e[k].sze; 33 upt(k); 34 k=y; 35 } 36 void Insert(int &k,const int &pre) 37 { 38 if(!k) 39 { 40 k=++pool;e[k].pri=pre;e[k].key=rand(); 41 e[k].same=e[k].sze=1;e[k].l=e[k].r=0; 42 return ; 43 } 44 else ++e[k].sze; 45 if(e[k].pri==pre) ++e[k].same; 46 else if(pre<e[k].pri) 47 { 48 Insert(e[k].l,pre); 49 if(e[e[k].l].key<e[k].key) 50 zig(k); 51 } 52 else 53 { 54 Insert(e[k].r,pre); 55 if(e[e[k].r].key<e[k].key) 56 zag(k); 57 } 58 return ; 59 } 60 void Delete(int &k,const int &pre) 61 { 62 if(e[k].pri==pre) 63 { 64 if(e[k].same>1) 65 { 66 --e[k].same; 67 --e[k].sze; 68 } 69 else if(!e[k].l||!e[k].r) 70 k=e[k].l+e[k].r; 71 else if(e[e[k].l].key<e[e[k].r].key) 72 { 73 zig(k); 74 Delete(k,pre); 75 } 76 else 77 { 78 zag(k); 79 Delete(k,pre); 80 } 81 return ; 82 } 83 --e[k].sze; 84 if(pre<e[k].pri) 85 Delete(e[k].l,pre); 86 else 87 Delete(e[k].r,pre); 88 return ; 89 } 90 int qianqu(const int &key) 91 { 92 int x=rt,res=-INF; 93 while(x) 94 { 95 if(e[x].pri<key) 96 { 97 res=e[x].pri; 98 x=e[x].r; 99 } 100 else 101 x=e[x].l; 102 } 103 return res; 104 } 105 int houji(const int &key) 106 { 107 int x=rt,res=INF; 108 while(x) 109 { 110 if(e[x].pri>key) 111 { 112 res=e[x].pri; 113 x=e[x].l; 114 } 115 else 116 x=e[x].r; 117 } 118 return res; 119 } 120 int di(int &k) 121 { 122 int x=rt; 123 while(x) 124 { 125 if(e[e[x].l].sze<k&&e[e[x].l].sze+e[x].same>=k) 126 return e[x].pri; 127 if(e[e[x].l].sze>=k) x=e[x].l; 128 else 129 { 130 k-=e[e[x].l].sze+e[x].same; 131 x=e[x].r; 132 } 133 } 134 return 0; 135 } 136 int piming(const int &key) 137 { 138 int x=rt,res=0; 139 while(x) 140 { 141 if(key==e[x].pri) 142 return res+e[e[x].l].sze+1; 143 if(key<e[x].pri) x=e[x].l; 144 else 145 { 146 res+=e[e[x].l].sze+e[x].same; 147 x=e[x].r; 148 } 149 } 150 return res; 151 } 152 int main() 153 { 154 scanf("%d",&n); 155 for(int i=1;i<=n;i++) 156 { 157 int opt,x; 158 scanf("%d%d",&opt,&x); 159 if(opt==1) 160 Insert(rt,x); 161 if(opt==2) 162 Delete(rt,x); 163 if(opt==3) 164 printf("%d ",piming(x)); 165 if(opt==4) 166 printf("%d ",di(x)); 167 if(opt==5) 168 printf("%d ",qianqu(x)); 169 if(opt==6) 170 printf("%d ",houji(x)); 171 } 172 return 0; 173 }