不知道开头写什么话
康康下面这个问题:
给定一个模式串和一个文本串,求模式串在文本串中出现的位置,次数.
一个显然的做法是对于文本串中的每个位置,都把模式串从头开始匹配.
但是这样的时间复杂度太高了,
所以我们有了接下来要讲的:kmp算法.
step 0
先定义一些东西.
(a):模式串.
(b):文本串.
(la):(a)的长度.
(lb):(b)的长度.
(next[i]):模式串中满足(a[1sim j]=a[i-j+1sim i])的最大的(j).
(f[i]):满足(a[1sim j]=b[i-j+1sim i])的最大的(j).
step 1
首先暴力的算法因为时间复杂度太高((O(la*lb)))而被抛弃...
所以我们要想想怎么排除掉一些多余的情况.
先举个例子:
(a):bababb.
(b):bababababababababb.
我们在第一次匹配的时候会是这样:
babab|b
babab|ababababababb
在第六位的时候失配了..
但是我们可以发现,前五位的(f[i])都已经求出来了.
如果我们采取暴力的做法,将(a)直接往后移一位时,就是这样:
|bababb
b|ababababababababb
可以发现在第一位就失配了,
所以对第六位没有任何帮助.
于是我们可以想想,
要怎样跳才能一步跳到有用的位置.
这时我们就需要这个next数组.
step 2
(首先next数组的定义我已经放上面了...)
假如我们已经求出了next数组(先别管怎么求的).
当我们匹配完第(i)位,且第(i)位在模式串中对应的是(j),
(就像上面的例子中,(i)=5,(j)=5)
而在第(i)+1位失配了.
于是我们就要改变(j),使(i+1)能匹配上.
而改变的方式就是把(j)改为(next[j]).
想一想这是为什么.
假设有一个(k>next[j]),使(a[1sim k+1]=b[i+1-(k+1)+1sim i+1]).
(因为我们这里是在求(i)+1,而(j)是与(i)匹配,所以(k)加了1)
即(k)对于(next[j])能使答案更优,
因为(i)是匹配上了的,所以(a[1sim j]=b[i-j+1sim i]).
因为(i+1)与(k+1)匹配上了,所以(i)与(k)也能匹配上,
即(a[1sim k]=a[i-k+1sim i]).
因此我们可以发现(a[1sim k]=a[j-k+1sim j]).
画个图理解一下(前面的不理解的可以自己画下图):
红色区域代表匹配了的部分.
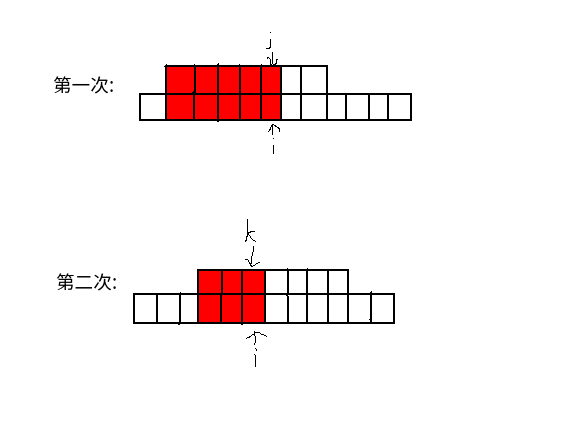
图片过于丑陋还请原谅.
回到正题,根据(next[j])的定义,这样的(k)是不存在的(否则(next[j])就等于(k))
因此直接跳到(next[j])肯定是更优的.
但是,(next[j])怎么求呢?
step 3
仔细康康(next)与(f)的定义,是不是非常像?
没错,我们就可以像求(f)一样,直接求(next).
就相当于自己与自己匹配一次.
code:
inline void getnext(){
Next[1]=0;
for(int i=2,j=0;i<=la;i++){
while(j>0&&a[i]!=a[j+1]) j=Next[j];
if(a[i]==a[j+1]) j++;
Next[i]=j;
}
}
所以,这个问题就解决了!
总的代码:
#include <iostream>
#include <cstdio>
#include <cstring>
#define fre(x) freopen(x".in","r",stdin),freopen(x".out","w",stdout)
using namespace std;
inline int read(){
int sum=0,f=1;char ch=getchar();
while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){sum=sum*10+ch-'0';ch=getchar();}
return f*sum;
}
const int N=1000005;
int T,la,lb,f[N],Next[N],ans;
char a[N],b[N];
inline void getnext(){
Next[1]=0;
for(int i=2,j=0;i<=la;i++){
while(j>0&&a[i]!=a[j+1]) j=Next[j];
if(a[i]==a[j+1]) j++;
Next[i]=j;
}
}
inline void kmp(){
for(int i=1,j=0;i<=lb;i++){
while(j>0&&(j==la||b[i]!=a[j+1])) j=Next[j];
if(b[i]==a[j+1]) j++;
f[i]=j;if(f[i]==la) ans++;
}
}
signed main(){
T=read();
while(T--){
scanf("%s%s",a,b);
la=strlen(a),lb=strlen(b);
for(int i=la;i>=1;i--) a[i]=a[i-1];
for(int i=lb;i>=1;i--) b[i]=b[i-1];
getnext();kmp();
printf("%d
",ans);ans=0;
}
return 0;
}