众所周知,线段树是一个非常好用也好写的数据结构,
因此,我们今天的前置技能:线段树.
然而,可持久化到底是什么东西?
别急,我们一步一步来...
step 1
首先,一道简化的模型:
给定一个长度为(n)的序列,(m)个操作,支持两种操作:
- 修改某个点(i)的权值
- 查询历史上某个版本(u)中点(i)的权值
同时,每个操作都会生成一个新的版本(也就是说修改是改的一个新的版本,而查询是直接(copy)上一个版本.
那么,暴力的做法来了:
直接维护(m)棵线段树,先(copy)一遍,再直接修改/查询.
然而时间空间都得炸啊啊啊
别急,让我们仔细想想...
首先,我们考虑一下每次修改会发生什么(看图):

(其中修改的是6号节点,红色是经过的路径),
我们可以发现,每次修改都只改了一条链.
也就是说,对于上一个版本,就只有一条链不一样(查询就是一模一样了).
因此,对于上一个版本中一样的其他的链,我们就可以直接沿用.
比如说,上一个版本长这样:
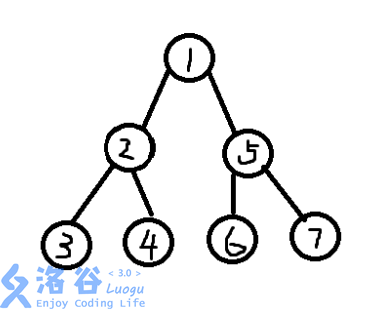
而沿用后的图就长这样选点时的随意导致了图片的丑陋:

那么,我们就只需要在更新版本时,新建一个根节点(rt[i]),
并且只需要新建修改的那条链,其他的沿用上一个版本的就行了.
代码也很简单:
void update(int &k/*动态加的点(当前节点)*/,int p/*沿用的点,即上个版本中这个位置的节点编号*/,int l,int r,int pla/*修改的元素位置*/,int x/*修改的权值*/){
k=++tot;t[k]=t[p];//先copy一波
if(l==r){t[k].val=x;return ;}
int mid=(l+r)>>1;//这里就和线段树一样了
if(pla<=mid) update(t[k].l,t[p].l,l,mid,pla,x);
else update(t[k].r,t[p].r,mid+1,r,pla,x);
}
顺便把建树和询问也贴上来吧(其实和线段树一样):
void build(int &x,int l,int r){
x=++tot;
if(l==r){t[x].val=a[l];return ;}
int mid=(l+r)>>1;
build(t[x].l,l,mid);build(t[x].r,mid+1,r);
}
int query(int p,int l,int r,int x){
if(l==r) return t[p].val;
int mid=(l+r)>>1;
if(x<=mid) return query(t[p].l,l,mid,x);
else return query(t[p].r,mid+1,r,x);
}
到这里,一个简单的模板就结束啦.
例题:[模板]可持久化数组
这题就和模板一模一样,
在叶子节点记录权值,每次单点修改即可.
注意一下,询问是复制的询问的那个版本(不是上一个)因为这个调了好久qwq
上完整代码吧其实都在上面了~:
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
inline int read(){
int sum=0,f=1;char c=getchar();
while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
while(c<='9'&&c>='0'){sum=sum*10+c-'0';c=getchar();}
return sum*f;
}
const int MX=1000005;
struct tree{int l,r,val;}t[MX*30];
int n,m,a[MX];
int rt[MX],tot=0;
void build(int &x,int l,int r){
x=++tot;
if(l==r){t[x].val=a[l];return ;}
int mid=(l+r)>>1;
build(t[x].l,l,mid);build(t[x].r,mid+1,r);
}
void update(int &k,int p,int l,int r,int pla,int x){
k=++tot;t[k]=t[p];
if(l==r){t[k].val=x;return ;}
int mid=(l+r)>>1;
if(pla<=mid) update(t[k].l,t[p].l,l,mid,pla,x);
else update(t[k].r,t[p].r,mid+1,r,pla,x);
}
int query(int p,int l,int r,int x){
if(l==r) return t[p].val;
int mid=(l+r)>>1;
if(x<=mid) return query(t[p].l,l,mid,x);
else return query(t[p].r,mid+1,r,x);
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++) a[i]=read();
build(rt[0],1,n);
for(int i=1;i<=m;i++){
int tt=read(),opt=read(),pla=read();
if(opt==1){int x=read();update(rt[i],rt[tt],1,n,pla,x);}
else if(opt==2){printf("%d
",query(rt[tt],1,n,pla));rt[i]=rt[tt];}
}
return 0;
}
step 2
接下来,就是我们喜闻乐见的主席树了(话说有哪位(dalao)能告诉我为什么叫这名字?).
我们以一道模板题开始吧:[模板]可持久化线段树 1(主席树)
给出一个长度为(n)的序列,(m)个询问,每次询问区间([l,r])中第(k)小的数.
这题暴力很好写吧(然而我们并不满足于暴力).
我们还是一步步来,
首先,先考虑下如果是区间([1,n])的第(k)小该怎么做:
这时候,我们可以考虑到权值线段树.
将原序列离散化,再建一棵线段树,
但这个线段树维护的区间并不是序列的区间,
而是权值的区间.
比如说区间([l,r]),其实指的是离散化后的权值(l)~(r),
也就是第(l)大到第(r)大.
还是举个栗子吧:
假设我们现在有一个序列(a):1,3,3,5,5,5,8,8,8,8.
那么离散化以后就是:1,2,2,3,3,3,4,4,4,4.
然后我们再建一棵权值线段树:

其中黑色的代表节点编号,红色的代表权值区间,
而蓝色的是接下来我们要讲的每个节点维护的一个值:(cnt).
这个(cnt)表示的是当前节点的权值区间内有几个节点.
听不懂?没关系我们接着看:
当我们讲第一个元素(在离散化后就是(1))插入以后,树就变成了这样:
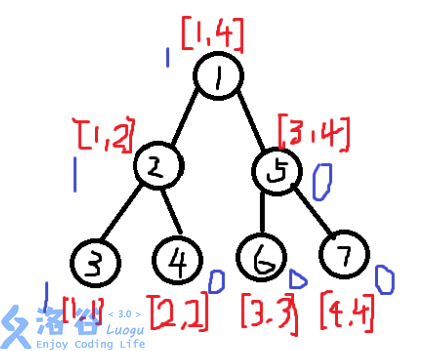
所有权值区间包括(1)的(cnt)都加了(1).
而当我们将所有数都插进去后,树就成了这样:
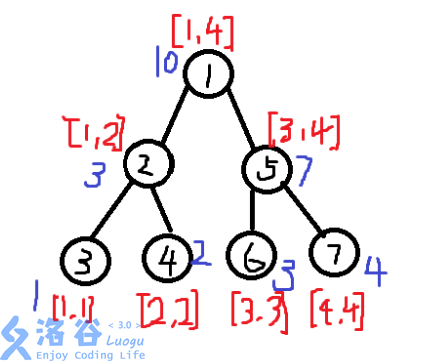
于是,我们就可以清楚地看到,在序列中,权值在区间([l,r])的数有多少个.
插入的代码如下:
int update(int p/*节点编号*/,int l,int r/*l,r为权值区间*/,int k/*插入的权值*/){
int x=++tot;t[x]=t[p];t[x].cnt++;
if(l==r) return x;
int mid=(l+r)>>1;
if(k<=mid) t[x].l=build(t[p].l,l,mid,k);
else t[x].r=build(t[p].r,mid+1,r,k);
return x;
}
然后我们在求第(k)小时,先与左子树的(cnt)比较,
若(k<=cnt),那答案就在左子树的权值区间里,
否则,将(k)减去(cnt),再在右子树里找,
一直到最底层就行了.
查询代码如下:
int query(int p/*当前节点*/,int l,int r,int k/*第k小*/){
if(l==r) return l;
int mid=(l+r)>>1;
if(k<=t[t[p].l].cnt) return query(t[p].l,l,mid,k);
else return query(t[p].r,mid+1,r,k-t[t[p].l].cnt);
}
那么接下来,我们来考虑区间([l,r])的第(k)小:
仔细想想,其实我们可以用前缀和的思想,
一个权值为(x)的数在(1)~(l-1)中出现了(a)次,
在(1)~(r)中出现了(b)次,
那么它在区间([l,r])中就出现了(a-b)次.
因此,我们可以对每个区间([1,i],iin [1,n])建一颗权值线段树,
在查询时,用前缀和的思想计算(cnt),再查找就行啦.
然而到这里就结束了吗?
我们注意到,对于区间([1,i])的权值线段树,
与区间([1,i-1])比起来仅仅是多插入了一个(i)的权值而已.
想到了什么? 可持久化线段树!
没错,我们可以像可持久化线段树一样,
沿用相同的节点,只新建需要更新的一条链就行了.
贴上新的询问代码:
int query(int L/*区间[1,l-1]的节点*/,int R/*区间[1,r]的节点*/,int l,int r,int k/*第k小*/){
if(l==r) return l;
int mid=(l+r)>>1,sum=t[t[R].l].cnt-t[t[L].l].cnt;//前缀和
if(sum>=k) return ask(t[L].l,t[R].l,l,mid,k);
else return ask(t[L].r,t[R].r,mid+1,r,k-sum);
}
到这里,主席树就讲完啦.
上完整代码吧:
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
inline int read(){
int sum=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){sum=sum*10+c-'0';c=getchar();}
return sum*f;
}
struct tree{int cnt,l,r;}t[5000001];
int n,m,a[1000001],c[1000001];
int rt[500001],tot=0;
int build(int p,int l,int r,int k){
int x=++tot;
t[x]=t[p];t[x].cnt++;
if(l==r) return x;
int mid=(l+r)>>1;
if(k<=mid) t[x].l=build(t[p].l,l,mid,k);
else t[x].r=build(t[p].r,mid+1,r,k);
return x;
}
int ask(int L,int R,int l,int r,int k){
if(l==r) return l;
int mid=(l+r)>>1,sum=t[t[R].l].cnt-t[t[L].l].cnt;
if(sum>=k) return ask(t[L].l,t[R].l,l,mid,k);
else return ask(t[L].r,t[R].r,mid+1,r,k-sum);
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++) a[i]=read();
memcpy(c,a,sizeof(c));sort(c+1,c+n+1);
int T=unique(c+1,c+n+1)-c-1;
for(int i=1;i<=n;i++) a[i]=lower_bound(c+1,c+T+1,a[i])-c;
for(int i=1;i<=n;i++) rt[i]=build(rt[i-1],1,T,a[i]);
for(int i=1;i<=m;i++){
int l=read(),r=read(),k=read();
printf("%d
",c[ask(rt[l-1],rt[r],1,T,k)]);
}
return 0;
}
以后可能还会更新(埋个坑在这)...
step 3
还真的更新了...
之前,我们讲了可持久化线段树的单点修改对吧.
然而,区间修改去哪了?
但是我们仔细想想,
对于每个版本的线段树,
它们是共用了一些节点,
所以在(pushdown) (tag)的时候,就会出锅...(自己(yy)一下就清楚了)
因此,我们有了一种新的操作——标记永久化.
将一个点的(tag)一直存下来,在询问的时候直接加上去.
而在修改的时候,只要被区间覆盖到,就要新建节点.
并且,还要一边切割需要修改的区间(这个等下看代码吧),
一直到完全重合时再返回.
来上修改和查询的代码吧:
int update(int p,int l,int r,int d){
int x=++tot;t[x]=t[p];
t[x].sum+=(r-l+1)*d;
if(t[x].l==l&&t[x].r==r){//完全重合时返回
t[x].tag+=d;return x;
}
int mid=(t[x].l+t[x].r)>>1;
if(r<=mid) t[x].ls=update(t[p].ls,l,r,d);//把要修改的区间切一下
else if(l>mid) t[x].rs=update(t[p].rs,l,r,d);
else t[x].ls=update(t[p].ls,l,mid,d),t[x].rs=update(t[p].rs,mid+1,r,d);
return x;
}
ll ask(int p,int ad/*一路加上的tag*/,int l,int r){
if(t[p].l==l&&t[p].r==r){
return (r-l+1)*ad/*别忘了tag*/+t[p].sum;
}
int mid=(t[p].l+t[p].r)>>1;
if(r<=mid) return ask(t[p].ls,ad+t[p].tag,l,r);
else if(l>mid) return ask(t[p].rs,ad+t[p].tag,l,r);
else return ask(t[p].ls,ad+t[p].tag,l,mid)+ask(t[p].rs,ad+t[p].tag,mid+1,r);
}
接下来,让我们来看道例题吧:洛谷SP11470 TTM - To the moon
这题就是标记永久化的板子了.
看代码吧:
#include <iostream>
#include <cstdio>
#include <cstring>
#define ll long long
using namespace std;
inline int read(){
int sum=0,f=1;char c=getchar();
while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9'){sum=sum*10+c-'0';c=getchar();}
return sum*f;
}
struct tree{int l,r,ls,rs;ll sum,tag;}t[2000021];
int n,m,a[500001];
int tt=0,tot=0,rt[500001];
inline void pushup(int p){
t[p].sum=t[t[p].ls].sum+t[t[p].rs].sum;
}
inline void build(int &p,int l,int r){
p=++tot;t[p].l=l;t[p].r=r;
if(l==r){t[p].sum=a[l];return ;}
int mid=(l+r)>>1;
build(t[p].ls,l,mid);build(t[p].rs,mid+1,r);
pushup(p);
}
int update(int p,int l,int r,int d){
int x=++tot;t[x]=t[p];
t[x].sum+=(r-l+1)*d;
if(t[x].l==l&&t[x].r==r){
t[x].tag+=d;return x;
}
int mid=(t[x].l+t[x].r)>>1;
if(r<=mid) t[x].ls=update(t[p].ls,l,r,d);
else if(l>mid) t[x].rs=update(t[p].rs,l,r,d);
else t[x].ls=update(t[p].ls,l,mid,d),t[x].rs=update(t[p].rs,mid+1,r,d);
return x;
}
ll ask(int p,int ad,int l,int r){
if(t[p].l==l&&t[p].r==r){
return (r-l+1)*ad+t[p].sum;
}
int mid=(t[p].l+t[p].r)>>1;
if(r<=mid) return ask(t[p].ls,ad+t[p].tag,l,r);
else if(l>mid) return ask(t[p].rs,ad+t[p].tag,l,r);
else return ask(t[p].ls,ad+t[p].tag,l,mid)+ask(t[p].rs,ad+t[p].tag,mid+1,r);
}
inline void change(){
int l=read(),r=read(),d=read();
rt[tt+1]=update(rt[tt],l,r,d);tt++;
}
inline void query(int x){
int l=read(),r=read(),opt=(x? read():tt);
printf("%lld
",ask(rt[opt],0,l,r));
}
inline void back(int x){
tt=x;tot=rt[x+1]-1;
}
int main(){
n=read();m=read();
for(int i=1;i<=n;i++) a[i]=read();
build(rt[0],1,n);
for(int i=1;i<=m;i++){
char opt[5];cin>>opt;
if(opt[0]=='C') change();
else if(opt[0]=='Q') query(0);
else if(opt[0]=='H'){query(1);}
else if(opt[0]=='B'){int x=read();back(x);}
}
return 0;
}