排序可谓是算法中最基本的基本问题,因为它不但可以拿出来来解决特定的排序问题,同时作为许多复杂的算法的子模块存在,在上几周中,我比较仔细的看了算法导论中中的排序部分,后面的习题中感觉有意思的也做了详细的思考,感觉很有收获。总体上还是按算法种类来写,堆排与快排看的最为仔细,写的也会多一点,比如快排的优化,如何减小快排的栈深度。而且像是快排,归并利用分治思想的算法,都十分适合进行多线程优化,我在学习过程中也进行了尝试。
基础较好的可以直接看堆排与快排部分。
关于算法的理解
先来说说我总体的一个感悟,排序的过程可以理解为不断了解序列中数之间的大小关系的过程,可以说不同的问题,其不同的实际意义赋予其不同的特性,比如排序的键值是否相同,范围如何,是离散的还是连续的,这些都会对排序产生影响。我们可以这样理解这种影响,假如是我们完全不知道有任何特性的序列,我们想要知道他们的次序要获取的信息量是一定的,具体的排序操作会为我们提供一定的信息量,问题原本的些特性也会为我们提供的一定的信息量,如何充分利用问题原本的条件提供的信息,加以合适步骤设计(平均每个操作为我们提供的信息较大),就可以认为是相对于此问题的较优的算法。 PS.很好奇有没有人利用信息论做过算法的研究。
优秀的算法设计应当是适配特定的问题的,而书本上经典的算法只能算作我们的素材,面对具体问题我们应该做出相应的改动,在下面应该会体现这一点。
插入排序
1.思路
思路是从序列的前端维护一个有序区,从无序区选择元素插入有序区,逐渐将有有序区扩大到是整个序列。 其中前端有序区就是我们的后面提到的用于证明的循环不变量。
2.伪码
INSERTION-SORT(A) for j = 2 to A.lenghth key = A[j] i = j - 1 while i > 0 and A[i] > key A[i+1] = A[i] i = i - 1 A[i] = key
3. 复杂度
时间复杂度
最好情况:
原本有序,只需O(n)
平均:
O(n2)
最差:
恰好逆序,O(n2)
空间复杂度
原址排序 O(1)
稳定性
稳定
这个作者放在了最前面,主要是想为读者理清行文的思路,同时讲解一些常用的技巧,如利用的循环不变式进行算法的证明:循环前不变式成立,循环中不变式成立,循环结束后不变式成立。
归并排序
1.思路
采用的是分治的思想,即将问题分解成几个原问题的子问题,然后递归的求解子问题,最后再将子问题的解合并,得到原问题的解。基本思路是不断将序列分为子序列,将子序列排好序,然后将他们合并起来。一般可以利用多线程方法优化。
2.伪码
MERGE(A,p,q,r) //A中p到q, q+1到r为排好序的子数组 n1 = q - p + 1 n2 = r - q for i = 1 to n1 L[i] = A[p+i-1] for j = 1 to n2 R[j] = A[q+j] L[n1+1] = flag //flag为一个足够大的值,充当哨兵,可以省去判空的逻辑 R[n2+1] = flag i = j = 1 for k = p to r if L[i] <= R[j] A[k] = L[i] i = i + 1 else A[k] = L[j] j = j + 1 MERGE-SORT(A,P,r) if(p < r) q = floor((p + r) / 2) MERGE-SORT(A,p,q) MERGE-SORT(A,q+1,r) MERGE(A,p,q,r)
3. 复杂度
时间复杂度
时间复杂度我们很容易由递推式
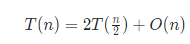
递归展开得到解为
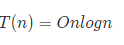
最好情况O(nlogn)
平均O(nlogn)
最差O(nlogn)
空间复杂度O(n)
这部分分析还是加入了我许多思考的,我们应该如何理解这个空间复杂度呢,递归算法其实占用的空间可以理解为两部分,一个是程序中开辟的空间,另一部分是递归函数压栈占据的空间(这也是快排空间复杂度最主要的部分),算法每次归并需要开辟新数组,其实底层的归并是占用不了多少空间的,因为递归较深的时候,需要归并的数组比较小,而我们讲的空间复杂复杂度应该是算法运行时间中占据的最大空间O(n),这明显发生在递归的最顶层,也就是归并A的整个左右时候开辟的数组,需要注意的是,此时是在递归的最顶层,所以没有占用递归压栈的空间,那么递归压栈的空间有没有可能超过这个量级呢,不可能的最大的栈深度是O(logn)的。
ps.此处讲道理应该是算严格计算压栈空间与开的临时数组的最大值的,但是我相信大家能看出来,很明显是递归结束时候总空间最大,虽然此时只有开辟的数组,你可以这样想,栈深度越深,开辟的数组大小下降速度是指数级别的。
堆排序
1.思路
这个原理一下还真说不清楚,但是下面的伪码应该不难看懂,当然前提是你对堆的性质确实比较熟悉,no bb ,show the code
2.伪码
MAX-HEAPIFY(A,i) //此函数作用是如果i的子孙节点满足堆性质,但是i本身不满足,通过调整i与其子孙的位置使其以i为根的树变成最大堆 l = left(i) //left与right直接定义为宏就行#define left = 2 * i r = right if l <= A.heap-size and A[l] > A[i] largest = l else largest = i if r <= A.heap-size and A[r] > A[i] largest = r if largest != i exchange A[i] with A[largest] MAX-HEAPIFY(A,largest) //调整largest为根的堆
MAX-HEAPIFY(A,i)//非递归版本,减少压栈的时间开销 largest = i while(i == largest ) l = left(i) r = right if l <= A.heap-size and A[l] > A[i] largest = l else largest = i if r <= A.heap-size and A[r] > A[i] largest = r if largest != i exchange A[i] with A[largest] i = largest //保证进入下一循环吗,调整以largest else largest = i + 1 //跳出循环
BUILD-MAX-HEAP(A) //建立一个最大堆 A.heap-size = A.length for i = floor(A.lenghth/2) down to 1 //从最大的有孩子节点向上调整 MAX-HEAPIFY(A,i) HEAP-SORT(A)
BUILD-MAX-HEAP(A) for i = A.length down to 2 exchange A[i] with A[1] //将堆顶点与最后的叶子节点进行置换 A.heap-size = A.heap-size - 1 //调节堆的大小 MAX-HEAPIFY(A,1) //因为置换打破了最小堆的性质。重新从顶点开始调整
3. 复杂度
时间复杂度
最好情况O(nlogn)
平均:O(nlogn)
最差O(nlogn)
空间复杂度
原址排序 O(1),注意要使用MAX-HEAPIFY的不递归版本,否则有O(logn)的栈空间损耗,面试回答O(1)
其实堆排序还是有很多东西可以说的,先说其时间复杂度分析,MAX-HEAPIFY(A,i) ,这个调整操作的复杂度很容易从递推式
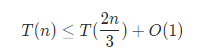
我看有人对于为何是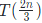 比较疑惑,书上说是恰好树的形状为半满,其实没说清楚,2/3其实还是树高为∞的一个极限。 我们很容易理解递归时候要递归子树的节点数占据总节点数目越多越好,不难想象要递归的孩子恰好比不递归的孩子多满满的一层最符合我们的要求而且树高越高,多的这一层占据的比例越大。
比较疑惑,书上说是恰好树的形状为半满,其实没说清楚,2/3其实还是树高为∞的一个极限。 我们很容易理解递归时候要递归子树的节点数占据总节点数目越多越好,不难想象要递归的孩子恰好比不递归的孩子多满满的一层最符合我们的要求而且树高越高,多的这一层占据的比例越大。
我们假设原来的树高为h数目为n,左子树为h-1,右子树为h-2,递归调整左子树,那么左子树的占比为:
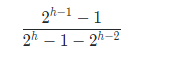
分母是假设右子树也为满的(即原树为高为h的完全二叉树),然后再减去最后一层的一半,在高h趋于无穷时候,极限为2/3。
不难求解,递推的答案为O(logn),即与树高成正比,注意这是最坏情况。
其后建堆的过程,从树的底层往上调用MAX-HEAPIFY(A,i),这个可以可以推出建堆的过程是O(n)的,之后的不断让A[1]与A[heap-size]调换,调用n次MAX-HEAPIFY(A,i)调整,故总体为O(nlogn),你或许会说,调整的时候,树高在降低吧,但是因为树接近完全二叉树,底层结点是比较多的,故不改变量级。
注意无论原数组如何,建堆之后的调整都是基本相同的,因为每次替代堆定点的元素都是较小的。因此最好最坏均值都在一个量级。
堆排小结
堆的非常好的性质就是,建堆之后,很多操作都可以在log(n)的复杂度进行,最经典的应用莫过于在一个大量级(假设为n)的数据中找出键值最大的k个,这时候最好的办法就是维护一个最小堆,每次碰到比堆中最小的要大的,当前元素换掉顶点,调用MAX-HEAPIFY(A,1)进行调整,问题复杂度为O(nlogk)
后面习题中有一个十分有意思的题目,有若干个大小为k的有序链表,这些链表的总元素数目为n,要求设计一个复杂度为O(nlogk)的算法。
我们必然是不能直接调用经典的排序算法的,因为会损失掉局部有序的信息,如何充分利用局部有序的条件呢,我们考虑这样一种算法,建立一个k大小的最大堆,第一次填充为各个有序序列的最大值(并在原序列中删除),然后建堆,将堆顶点弹出到输出序列,从取顶点的有序序列再取出第二大的点插到顶点处,调用MAX—HEAPIFY(A,1)调整,循环往复,直到各个有序序列都变为空,再将堆进行排序,插入到输出序列的后面,不能看出,时间复杂度由调用MAX—HEAPIFY(A,1)的次数决定,调用大概n次,每次调整复杂度为logk,得解。