
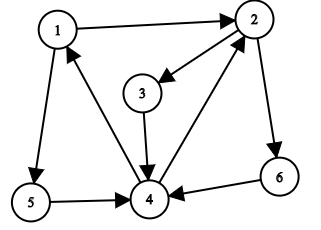

题意:n个顶点、m条边组成的有向图中,每条边默认距离为1,人要走一条长为k的路径,所经过节点的编号已确定(在p数组中,人从p[0]走到p[k-1])。
人在走的时候,有一个导航仪,会实时给出 当前位置 c 到目的地 t 的最短路径之一。
若人下一步到达的节点 与 导航仪给出的下一步节点不同,则导航仪会再重新生成下一步到达节点 与 目的地 t 的最短路径之一。
因为在存在多条最短路径时,导航仪会随机给出一条最短路径,所以当人按照规定路径走时,导航仪重新生成路径的次数不定。
求导航仪重新生成路径的最少次数 和 最多次数。
题解:1. 求导航仪重新生成路径的次数,其实就是求人在走每一步时,是否是沿着当前点到目标点的最短路径,所以需要求其他点到目标点的最短路径或者最短距离。
显然,求到固定点的最短距离有熟悉的Dijkstra算法、SPFA算法,而求最短路径(获得完整路径所经过的所有点)并不是容易的事情。
所以我们可以转化为:下一步所走点 到 目标点的距离,是否为 所有从当前点可到达的点中 与目标点距离最小的点。
n和m都是2*10^5数量级,显然用邻接表(链式前向星)来存储整个图。
边权值为1,没有负权值,可以直接用堆优化的Dijkstra算法。(不用堆优化是O(n^2),优化后O(mlog(n)) )
2. 因为Dijkstra算法求的是从源点到其他点的距离,而我们要的是从其他点到终点的距离,所以应该在反图(每条边的方向都置反)中进行。
而求出所有点到终点的距离数组 d 后,我们需要从起点沿着原来的图检查一遍,看看每一步所到的点 是否为 当前点可到达的所有点中d数组值最小的;
若是唯一的最小值(即是唯一的最短路径上的点)时,那么导航仪一定不需要Rebuild;
若是最小值之一(即是最短路径之一上面的点)时,那么导航仪可能要Rebuild,也可能不需要;
若不是最小值(即不是最短路径上的点)时,那么导航仪一定需要Rebuild。
详细见代码和注释如下:
#include<cstdio> //scanf,printf #include<cstring> //memcpy,memset,strcpy #include<vector> //lower_bound, unique #include<cmath> //log,acos #include<algorithm> //sort #include<iostream> //cin,cout #include<map> #include<string> //string #include<utility> //pair #include<queue> #include<functional> //greater,less using namespace std; const int maxn = 2e5 + 1; struct Graph { int head[maxn], nxt[maxn], to[maxn], tot; void add_edge(int u, int v) { to[++tot] = v; nxt[tot] = head[u]; head[u] = tot; } }G1, G2; //需要建正图和反图 int p[maxn], d[maxn]; bool vis[maxn]; //因为Dijkstra算法是算从源点到其他点的距离,而本题需要求其他点到终点的距离 void dijkstra(int st) { //所以在反图上跑,求得 其它点到终点的距离 memset(d, 0x3f, sizeof d); //memset(vis, 0, sizeof vis); 只执行一次时可以省略这行 priority_queue< pair<int, int>>q; //默认是大根堆 q.push({ 0,st }); d[st] = 0; while (!q.empty()) { int x = q.top().second; q.pop(); if (vis[x])continue; //保证只出堆一次,(每个节点只被用来更新一次) vis[x] = true; for (int i = G2.head[x]; i; i = G2.nxt[i]) { int y = G2.to[i]; if (d[y] > d[x] + 1) { d[y] = d[x] + 1; q.push({ -d[y],y }); //距离的符号变反,就成了距离的小根堆。y可以被push进多次,参与比较 } } } } int main() { int n, m, k; ios::sync_with_stdio(false); cin >> n >> m; for (int i = 0; i < m; i++) { int u, v; cin >> u >> v; G1.add_edge(u, v); //建立正图 G2.add_edge(v, u); //建立反图 } cin >> k; for (int i = 0; i < k; i++) { cin >> p[i]; } dijkstra(p[k - 1]); //求出其他点到终点的距离d int ansmx(0), ansmn(0); for (int i = 1; i < k; i++) { //在正图上走一遍 int id = p[i]; int maybe = 2; //p[i]是唯一的最短路径 for (int j = G1.head[p[i - 1]]; j; j = G1.nxt[j]) { //正图上可以获得正确的可走点 信息 int y = G1.to[j]; if (y == id)continue; //记得过滤掉p[i]本身 if (d[y] < d[id]) { //p[i]不是最短路径 maybe = 0; break; } else if (d[y] == d[id])maybe = 1; //p[i]是最短路径之一 } if (maybe == 0) { //p[i]不是最短路径 ansmx++; ansmn++; } else if (maybe == 1) { //p[i]是最短路径之一(还有其他最短路径) ansmx++; } //else{ 都不变;} //maybe = 2,p[i]是唯一的最短路径 } printf("%d %d", ansmn, ansmx); return 0; }