问题的提出:如何在10亿数中找出前1000大的数?
解决方案:
这是经典的TopN问题,先想到的时先排序,然后取前1000个数。部分排序,只排除前1000个数即可,但这两种方法的时间复杂度都比较高。
分治法,类似快速排序中的epartition的操作,随机选一个数t,然后对整个数组进行partition,会得到两部分,前一部分的数都大于t,后一部分的数都小于t。

如果说前一部分总数大于1000个,那就继续在前一部分进行partition寻找。如果前一部分的数小于1000个,那就在后一部分再进行partition,寻找剩下的数。

分治法的时间复杂度为O(n)。首先,partition的过程,时间是o(n)。我们在进行第一次partition的时候需要花费n,第二次partition的时候,数据量减半了,所以只要花费n/2,同理第三次的时候只要花费n/4,以此类推。而n+n/2+n/4+...显然是小于2n的,所以这个方法的渐进时间只有o(n)。

分治法的优化处理:

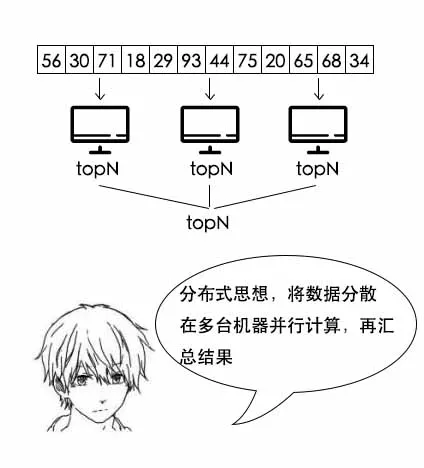







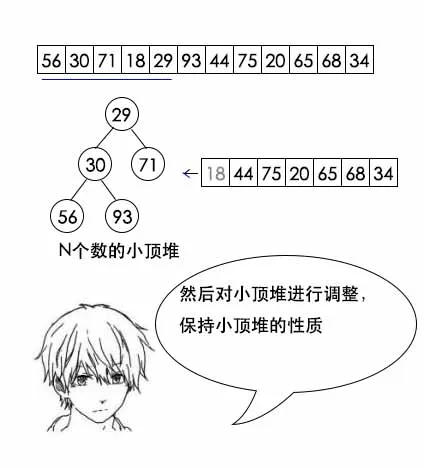
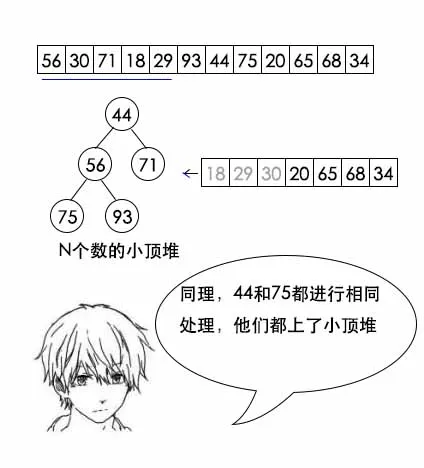
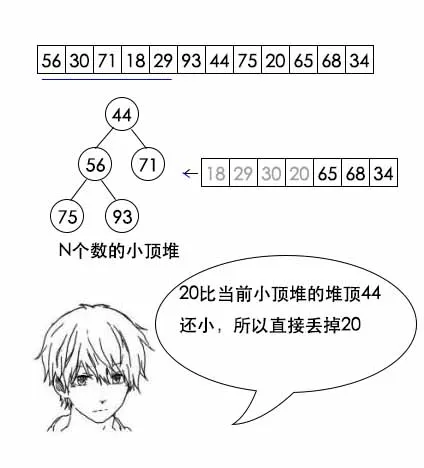



1 import java.util.Arrays; 2 3 public class TopN { 4 // 父节点 5 private int parent(int n) { 6 return (n - 1) / 2; 7 } 8 9 // 左孩子 10 private int left(int n) { 11 return 2 * n + 1; 12 } 13 14 // 右孩子 15 private int right(int n) { 16 return 2 * n + 2; 17 } 18 19 // 构建堆 20 private void buildHeap(int n, int[] data) { 21 for(int i = 1; i < n; i++) { 22 int t = i; 23 // 调整堆 24 while(t != 0 && data[parent(t)] > data[t]) { 25 int temp = data[t]; 26 data[t] = data[parent(t)]; 27 data[parent(t)] = temp; 28 t = parent(t); 29 } 30 } 31 } 32 33 // 调整data[i] 34 private void adjust(int i, int n, int[] data) { 35 if(data[i] <= data[0]) { 36 return; 37 } 38 // 置换堆顶 39 int temp = data[i]; 40 data[i] = data[0]; 41 data[0] = temp; 42 // 调整堆顶 43 int t = 0; 44 while( (left(t) < n && data[t] > data[left(t)]) 45 || (right(t) < n && data[t] > data[right(t)]) ) { 46 if(right(t) < n && data[right(t)] < data[left(t)]) { 47 // 右孩子更小,置换右孩子 48 temp = data[t]; 49 data[t] = data[right(t)]; 50 data[right(t)] = temp; 51 t = right(t); 52 } else { 53 // 否则置换左孩子 54 temp = data[t]; 55 data[t] = data[left(t)]; 56 data[left(t)] = temp; 57 t = left(t); 58 } 59 } 60 } 61 62 // 寻找topN,该方法改变data,将topN排到最前面 63 public void findTopN(int n, int[] data) { 64 // 先构建n个数的小顶堆 65 buildHeap(n, data); 66 // n往后的数进行调整 67 for(int i = n; i < data.length; i++) { 68 adjust(i, n, data); 69 } 70 } 71 72 // 打印数组 73 public void print(int[] data) { 74 System.out.println(Arrays.toString(data)); 75 } 76 }
1 import java.util.Random; 2 3 public class Main { 4 5 public static void main(String[] args) { 6 7 TopN topN = new TopN(); 8 9 // 第一组测试 10 int[] arr1 = new int[]{56, 30, 71, 18, 29, 93, 44, 75, 20, 65, 68, 34}; 11 12 System.out.println("原数组:"); 13 topN.print(arr1); 14 topN.findTopN(5, arr1); 15 System.out.println("调整后数组:"); 16 topN.print(arr1); 17 18 // 第二组测试 19 int[] arr2 = new int[1000]; 20 for(int i=0; i<arr2.length; i++) { 21 arr2[i] = i + 1; 22 } 23 24 System.out.println("原数组:"); 25 topN.print(arr2); 26 topN.findTopN(50, arr2); 27 System.out.println("调整后数组:"); 28 topN.print(arr2); 29 30 // 第三组测试 31 Random random =new Random(); 32 int[] arr3 = new int[1000]; 33 for(int i=0; i<arr3.length; i++) { 34 arr3[i] = random.nextInt(); 35 } 36 37 System.out.println("原数组:"); 38 topN.print(arr3); 39 topN.findTopN(50, arr3); 40 System.out.println("调整后数组:"); 41 topN.print(arr3); 42 } 43 }
运行结果:
