Uva10870 Recurrences（矩阵快速幂）

题目

考虑递推关系式(f(n)=a1*f(n-1)+a2*f(n-2)+....+ad*f(n-d))，计算f(n)%m

【输入格式】 输入包含多组测试数据。每组数据第一行为三个整数d,n,m(1<=d<=15,1<=n<=2^31-1,1<=m<=46340)。第二行包含d个非负整数a1,a2.....ad。第三行为d个非负整数f(1),f(2).....f(d)。这些数字均不超过2^31-1。输入结束的标志是d=n=m=0.

【输出格式】 对于每组数据，输出f(n)%m

思路

前置知识是矩阵乘法和矩阵快速幂。

矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的栏数（column）和第二个矩阵的列数（row）相同时才有定义。一般单指矩阵乘积时，指的便是一般矩阵乘积。若A为m×n矩阵，B为n×p矩阵，则他们的乘积AB会是一个m×p矩阵。

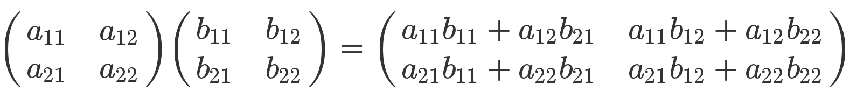
公式：

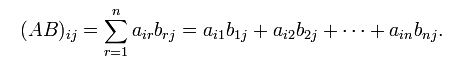
而矩阵快速幂对于n*n的方针多次进行自己乘自己的迭代运算，同样可以用数的快速幂优化。

举例来说，对于本题而言

设(F[n]=(f[n-d+1],f[n-d+2],f[n-d+3]....f[n]))

接下来要构造矩阵A，使得(F[n]=F[n-1]*A)

简单笔算一下可知：

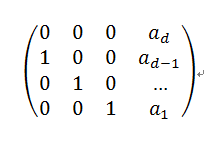
这样代码也不难写出了，注意：矩阵相乘不满足交换律！！！！

代码

#include<bits/stdc++.h>
#define M 25
#define LL long long
using namespace std;
int d,x,mod;
struct Matrix{
	int n,m,a[M][M];
	void clear(){memset(a,0,sizeof(a));}
	void resize(int _n,int _m){n=_n;m=_m;}
	Matrix operator *(const Matrix &_)const{
		Matrix res;res.resize(n,_.m);
		for(int i=1;i<=n;i++){
			for(int j=1;j<=_.m;j++){
				res.a[i][j]=0;
				for(int k=1;k<=m;k++){
					res.a[i][j]+=1LL*a[i][k]*_.a[k][j]%mod;
					if(res.a[i][j]>=mod)res.a[i][j]-=mod;	
				}
			}
		}
		return res;
	}
}Ma,F_d;
Matrix qkpow(Matrix a,int b){
	Matrix res;res.clear();res.resize(a.n,a.n);
	for(int i=1;i<=a.n;i++)res.a[i][i]=1;
	while(b){if(b&1)res=res*a;a=a*a;b>>=1;}
	return res;
}
int A[M],f[M];
int main(){
	while(scanf("%d%d%d",&d,&x,&mod)&&(d!=0&&x!=0&&mod!=0)){
		for(int i=1;i<=d;i++)scanf("%d",&A[i]),A[i]%=mod;
		for(int i=1;i<=d;i++)scanf("%d",&f[i]),f[i]%=mod;
		if(x<=d){printf("%d
",f[x]);continue;}
		Ma.clear();Ma.resize(d,d);
		for(int i=2;i<=d;i++)Ma.a[i-1][i]=1;
		for(int i=1;i<=d;i++)Ma.a[d][i]=A[d-i+1];
		F_d.clear();F_d.resize(d,1);
		for(int i=1;i<=d;i++)F_d.a[i][1]=f[i];
		Matrix ans=qkpow(Ma,x-d)*F_d;
		printf("%d
",ans.a[d][1]);
	}
	return 0;
}