遗传算法

遗传算法的思想

• 模拟物种进化的过程，来求解一个较优的可行解。

遗传算法的特点

       优点：具有普适性，可以解决的问题涵盖范围较广。

       缺点：求解的问题为近似的数值解，对于经典数学可以解决的问题效率比较低。

遗传算法解决问题具体步骤

问题：求下述二元函数的最大值：f(x,y) = x^2 + y^2 ，其中x,y ∈ {1,2,3,4,5,6,7}。

（一）个体编码

       遗传算法的运算对象是表示个体的字符串。所以必须把变量 x , y编码为一种符号串。

       由于在此问题中，x,y 为 0~7之间的整数，所以分别用3位无符号二进制整数来表示，将它 们连接在一起所组成的6位无符号二进制数，可以表示一个可行解。

       例如，基因型 X＝101110 所对应的表现型是：x＝[ 5，6 ]。

（二）初始群体的产生

       遗传算法是对群体进行的进化操作，需要给其淮备一些表示起始搜索点的初始群体数据。

       本例中，群体规模的大小取为4，即群体由4个个体组成，每个个体可通过随机方法产生。

       本例中产生的初始群体为：011101，101011，011100，111001。

（三）适应度计算

       遗传算法中以个体适应度的大小来评定各个个体的优劣程度，从而决定其遗传机会的大小，适应度决定了群体的进化方向。

       本例中直接使用目标函数值作为个体的适应度。

（四）选择运算

       选择运算(或称为复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。一般要求适应度较高的个体将有更多的机会遗传到下一代群体中。

        本例中，我们采用与适应度成正比的概率来确定各个个体复制到下一代群体中的数量。具体操作为：

• 先计算出群体中所有个体的适应度的总和 Σf_i ( i=1.2,…,M )。
• 其次计算出每个个体的相对适应度的大小 f_i / Σf_i ，它即为每个个体被遗传到下一代群体中的概率。
• 每个概率值组成一个区域，全部概率值之和为1。
• 最后再产生一个0到1之间的随机数，依据该随机数出现在上述哪一个概率区域内来确定各个个体被遗传到下一代群体的次数。

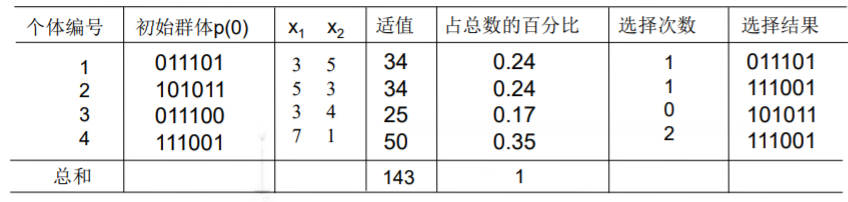
       选择结果即为下一代群体的初始组成，其在某种程度上就相当于此代群体中繁育下一代的父母基因类型集合。

（五）交叉运算

        交叉运算是遗传算法中产生新个体的主要操作过程，它以某一概率相互交换某两个个体之间的部分染色体。

        本例采用单点交叉的方法，其具体操作过程是：

• 先对群体进行随机配对。
• 其次随机设置交叉点位置。
• 最后再相互交换配对染色体之间的部分基因。

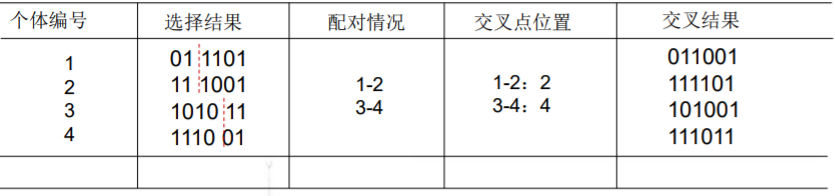
       交叉结果即为下一代群体的初始组成，其在某种程度上就相当于此代群体中繁育下一代的受精卵形成过程中染色分配。

（六）变异运算

       变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进行改变，它也是产生新个体的一种操作方法。

       本例中，我们采用基本位变异的方法来进行变异运算，其具体操作过程是：

• 首先确定出各个个体的基因变异位置，下表所示为随机产生的变异点位置， 其中的数字表示变异点设置在该基因座处。
• 然后依照某一概率将变异点的原有基因值取反。

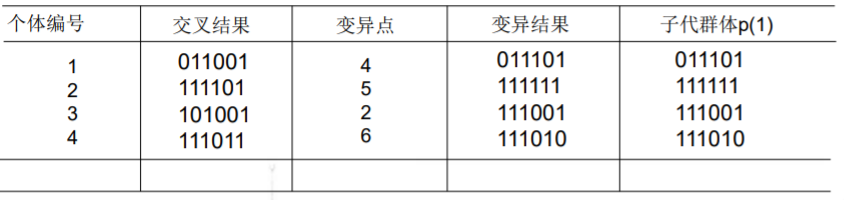
       最终产生的群体即为子代群体的最终版。变异操作相当于此代群体中繁育下一代中的基因变异等生物现象。

注：在实际应用中，这一过程并不是会像所给例子一样会产生如此优秀的结果，而是需要进行大量的运算得到大量的结果，在大量结果中挑选较优的部分。