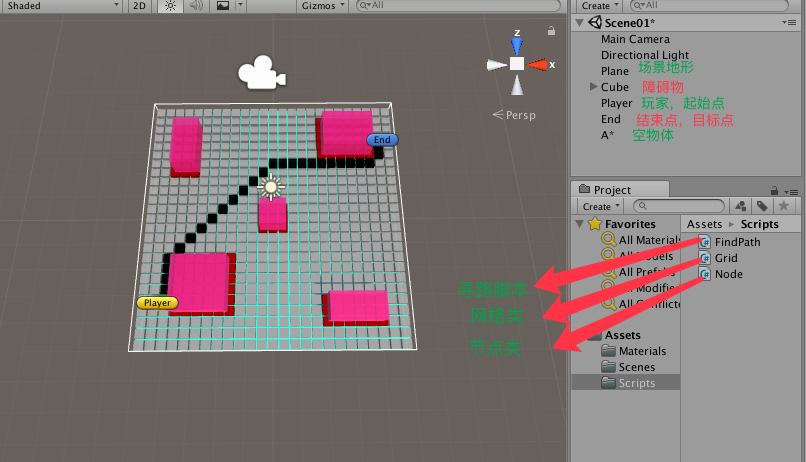
下面就介绍一个简单案例,帮助我们更好得了解A* 算法。

从Player到end根据两者之间的位置关系以及他们中间的障碍物的位置,通过计算找到一条最优路径,并将路径渲染成黑色。
节点类:用来实例化节点,即每一个格子,节点所附带的属性有,是否可行走、节点在世界坐标中的实际位置、节点对应的网格下标、以及当前节点的fgh值
public class Node { //判断当前格子是否可走 public bool _canWalk; //用来保存节点的位置‘ public Vector3 _worldPos; //当前节点对应的网格下标 public int _gridX, _gridY; //节点与起始点的距离 public int gCost; //节点与目标点的位置 public int hCost; //表示g+h,为当前节点塑造格子的开销 public int fCost { get { return gCost + hCost; } } //声明当前节点对应格子父节点 public Node parent; //构造方法 /// <summary> /// 构造方法 /// </summary> /// <param name="canWalk">If set to <c>true</c> 当前格子是否可行走</param> /// <param name="postion">当前格子对应节点的世界坐标.</param> /// <param name="x">格子在二维数组里的x值</param> /// <param name="y">格子在二维数组里的y值</param> public Node (bool canWalk, Vector3 postion, int x, int y) { _canWalk = canWalk; _worldPos = postion; _gridX = x; _gridY = y; } }
脚本Grid,挂在A*空物体上,用于在地形上渲染格子,和处理格子的颜色
/// <summary> /// 网格脚本,用于将地面划分成多个网格,存放在二维数组中,方便计算 /// 创建节点 /// </summary> public class Grid : MonoBehaviour { //定义存储格子的集合 public Node[,] grid; //定义整个地形的网咯尺寸 public Vector2 mapSize = new Vector2 (10f, 10f); //定义节点的半径 public float nodeRadius = 0.2f; //节点的直径 public float nodeDiamete; //用于表示节点实在可行走层还是不可行走的层 public LayerMask walkLayer; //根据整个地形网格的宽度和节点半径来计算每个方向上有多少个网格 //即二维数组的长度和宽度 public int gridCountX, gridCountY; //玩家所在位置 public Transform player; //用来保存正确路径的列表 public List<Node> path = new List<Node> (); void Start () { //计算出直径 nodeDiamete = nodeRadius * 2; //计算出当前有多少个格子,用来初始化二维二维数组 //Mathf.RoundToInt :将结果转成int类型 四舍五入 gridCountX = Mathf.RoundToInt (mapSize.x / nodeDiamete); gridCountY = Mathf.RoundToInt (mapSize.y / nodeDiamete); //根据获得水平和垂直方向上的格子数初始化数组 grid = new Node[gridCountX, gridCountY]; //创建节点 CreatNode (); } //创建节点 void CreatNode () { //后的整个地形左下角格子的左下角坐标 Vector3 startPos = transform.position - mapSize.x / 2 * Vector3.right - mapSize.y / 2 * Vector3.forward; //变量二维数组 for (int i = 0; i < gridCountX; i++) { for (int j = 0; j < gridCountY; j++) { //每个节点的实际位置,应该是每个格子的中心点 //起始点+右边和前边的偏移量→_→ Vector3 worldPoint = startPos + Vector3.right * (i * nodeDiamete + nodeRadius) + Vector3.forward * (j * nodeDiamete + nodeRadius); //从当前节点的位置开始,以节点的半径为半径,去检测该节点是否会碰到碰撞器 bool canWalk = !Physics.CheckSphere (worldPoint, nodeRadius, walkLayer); //实例化 grid [i, j] = new Node (canWalk, worldPoint, i, j); } } }
该方法为Unity系统自动回调的方法,用于绘制不同形状的线框。
//画出网格的边缘,OnDrawGizmos在每帧调用一次,只在scene可见 void () { //以平面的中心为所在位置,画出立方体 Gizmos.DrawWireCube (transform.position, new Vector3 (mapSize.x, 1, mapSize.y)); //根据玩家的位置得到玩家所在格子的节点【寻路的起始点】 Node playerNode = GetNodeFromPosition (player.position); //遍历可行走的区域标记为白色,否则红色 foreach (Node node in grid) { Gizmos.color = node._canWalk ? Color.white : Color.red; //在每一个node所在的位置画一个立方体 Gizmos.DrawCube (node._worldPos, Vector3.one * (nodeDiamete - 0.05f)); } if (playerNode == null) { //如果没有起始点 return; } //画出路径 if (path != null) { //遍历路径数组 foreach (Node node in path) { //计算后的最优路径显示为黑色 Gizmos.color = Color.black; //画出路径 Gizmos.DrawCube (node._worldPos, Vector3.one * (nodeDiamete - 0.05f)); } } //画出Player所在的地方 if (playerNode._canWalk) { Gizmos.color = Color.green; Gizmos.DrawCube (playerNode._worldPos, Vector3.one * (nodeDiamete - 0.05f)); } } //根据世界坐标的位置,获取到二维数组中某一个对应节点(格子) public Node GetNodeFromPosition (Vector3 pos) { //算出pos的坐标在整个网格中的纵横方向的百分比 float percentX = (pos.x + mapSize.x / 2) / mapSize.x; float percentY = (pos.z + mapSize.y / 2) / mapSize.y; //确保比例是在0-1之间的数 percentX = Mathf.Clamp01 (percentX); percentY = Mathf.Clamp01 (percentY); //通过比例得到所在格子的下标 int x = Mathf.RoundToInt ((gridCountX - 1) * percentX); int y = Mathf.RoundToInt ((gridCountY - 1) * percentY); //根据下标找到对应的Node Node node = grid [x, y]; Debug.Log ("x = " + x + " , y = " + y); return node; } //获取指定节点周围的节点 public List<Node> GetNeibourNode (Node node) { List<Node> nodes = new List<Node> (); for (int i = -1; i <= 1; i++) { for (int j = -1; j <= 1; j++) { if (i == 0 && j == 0) { continue; } int x = node._gridX + i; int y = node._gridY + j; //检测是否越界 if (x >= 0 && x < gridCountX && y >= 0 && y < gridCountY){ //将节点加入集合 nodes.Add (grid [x, y]); } } } return nodes; /*//左下 nodes.Add (grid[x-1,y-1]); //正下 nodes.Add (grid[x,y-1]); //右下 nodes.Add (grid[x+1,y-1]); //右 nodes.Add (grid[x+1,y]); //右上 nodes.Add (grid[x+1,y+1]); //正上 nodes.Add (grid[x,y+1]); //左上 nodes.Add (grid[x-1,y+1]); //左 nodes.Add (grid[x-1,y]);*/ } } 脚本FindPath:核心脚本,实现寻路算法 public class FindPath : MonoBehaviour { //玩家的位置和终点的位置 public Transform player, endPoint; //地图格子脚本 Grid grid; void Start () { //获得格子脚本 grid = GetComponent<Grid> (); } void Update () { //寻路 FindingPath (player.position, endPoint.position); }
算法核心:实现在起始点和终点之间计算得到一条最短路径
计算最优路径的方法:从开始节点开始,遍历其周边的8个点,找到开销最小的作为路径节点,再遍历新该节点,直到遍历到周围的子节点中有一个时结束节点时。这时从后往前回溯节点,生成一条路径,该路径便是从起始点到终点的最优路径。
void FindingPath (Vector3 startPos, Vector3 endPos) { //通过起始点和终止点的位置获得对应的节点 Node startNode = grid.GetNodeFromPosition (startPos); Node endNode = grid.GetNodeFromPosition (endPos); //开启列表和关闭列表 List<Node> openSet = new List<Node> (); List<Node> closeSet = new List<Node> (); //将起始点先加入到openSet中 openSet.Add (startNode); 该遍历循环的作用就是每一次遍历一个节点周边的8个节点,找到其中开销最小的存入关闭列表中,不停循环直至找到结束节点 //通过循环遍历找出开启列表中,消耗值最小的节点 while (openSet.Count > 0) { //当前节点 Node currentNode = openSet [0]; //遍历如果当前节点的开销f小于当前节点的开销f或者等于当前节点的 //开销f并且开启列表中节点距离目标点h小于当前节点的h,这时,我们更换 //这个列表中的节点为当前节点 for (int i = 0; i < openSet.Count; i++) { if (openSet [i].fCost < currentNode.fCost || openSet [i].fCost == currentNode.fCost && openSet [i].hCost < currentNode.hCost) { //更新当前节点 currentNode = openSet [i]; } } //从开启列表移除当前节点 openSet.Remove (currentNode); //将其加入关闭列表 closeSet.Add (currentNode); //如果当前节点时结束节点 if (currentNode == endNode) { GeneratePath (startNode, endNode); //已经查找到最优路径,结束查询 return; } //遍历当前节点周围的8个节点(当前节点已经是开销f最小的节点) foreach (Node node in grid.GetNeibourNode(currentNode)) { //如果节点不能走,或者该节点已经在关闭列表中 if (!node._canWalk || closeSet.Contains (node)) { continue; } //计算当前节点到开始节点的距离+当前节点到结束节点之间的距离 int newCost = currentNode.gCost +GetDistanceBetweenTwoNode (currentNode, node); //判断新的开销和原来开销之间的大小关系 if (newCost < node.gCost || !openSet.Contains (node)) { node.gCost = newCost; //获得这个节点的预估值h node.hCost = GetDistanceBetweenTwoNode (node, endNode); //将这个节点父物体设置为当前节点 node.parent = currentNode; //如果node没有在开启列表中,加入进去 if (!openSet.Contains (node)) { openSet.Add (node); } } } } }
//该方法计算的是某一个节点的h值,即从该节点到终点的期望距离
//得到两个节点之间的距离 int GetDistanceBetweenTwoNode (Node a, Node b) { //横轴上间隔的格子 int x = Mathf.Abs (a._gridX - b._gridX); //纵轴上间隔的格子 int y = Mathf.Abs (a._gridY - b._gridY); //表示横轴上间隔的格子数目比纵轴上的多 if (x > y) { return 14 * y + 10 * (x - y); } else { return 14 * x + 10 * (y - x); } } 通过遍历节点的父节点,由父子关系一层一层的回溯上去,最终得到一条消耗最小的路径 void GeneratePath (Node startNode, Node endNode) { List<Node> path = new List<Node> (); //从最终节点中其父节点,回溯到起始节点 Node temp = endNode; while (temp != startNode) { //将该节点放到path中 path.Add (temp); temp = temp.parent; } //将路径列表反转,因为路径要从开始节点开始 path.Reverse (); //将生成的路径赋值给最优路径 grid.path = path; } }
