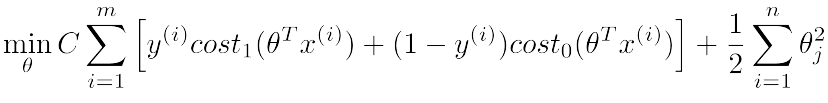Support Vector Machine(支持向量机)
Optimization objective(优化目标)
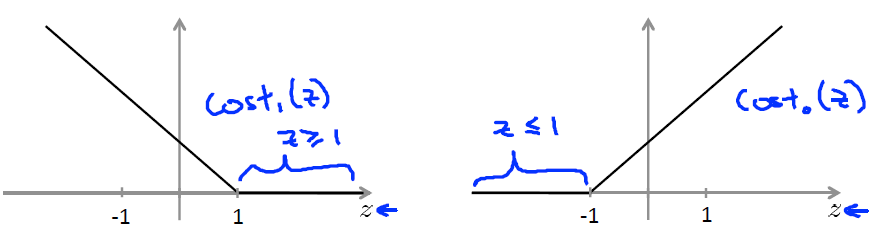
1.cost函数,下图左右分别对应于y取值1和0时的函数曲线,并且均有两段线组成
2.相对于逻辑斯蒂回归,没有了(1/m)项
3.正则部分不含有lambda值
4.拟合损失部分包含C项,相当于(1/lambda)的作用,一般取值很大
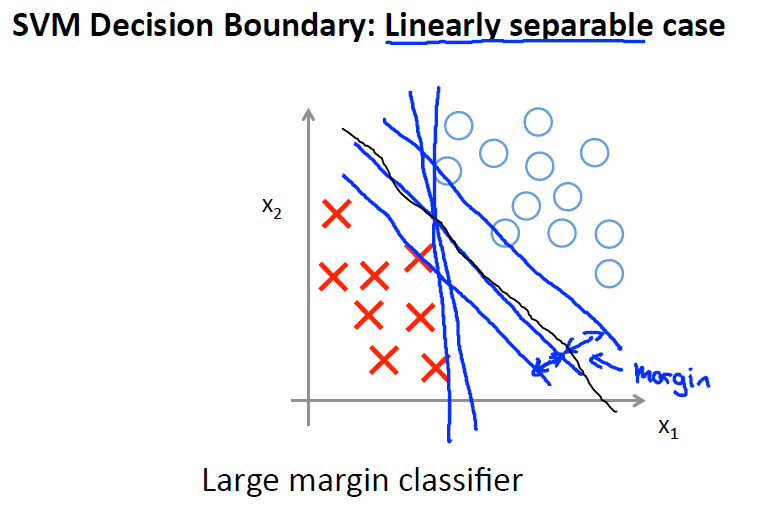
Large Margin Intuition(宽分类边距)
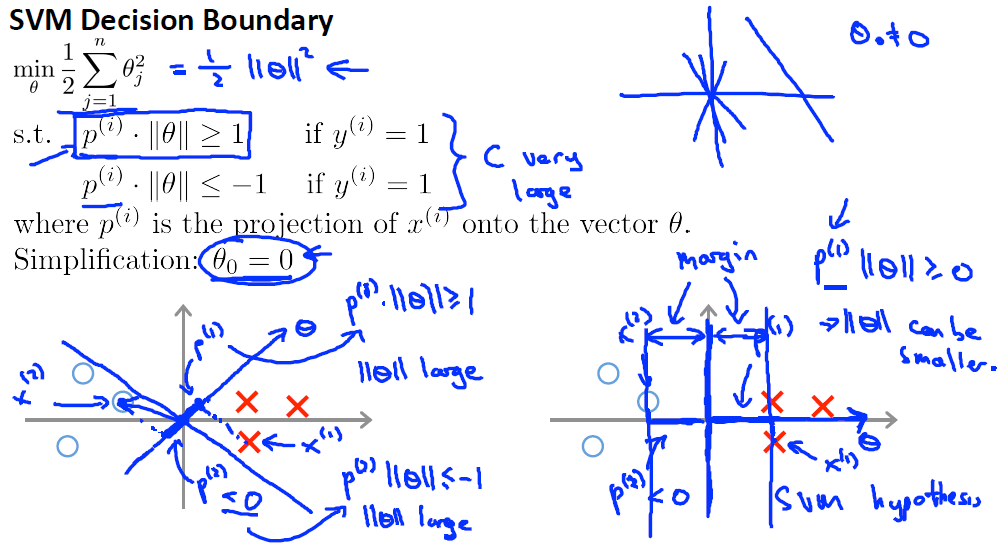
一般分类阈值要求:
实现:
两种情况:C值not large时,分类边界区域类间中心位置,对特殊个例值有较好忽略作用,C值very large时,不具有这种效应, lambda很小。
数学证明
简单理解:C值很大时,相当于拟合损失部分权值很大,为了最小化损失函数值,正则化部分趋于很小,即||θ||取值很小,同时在计算
时,为了使其绝对值大小满足分类要求,则要求θ方向与主体实验数据方向趋于一致,同时在分界线与θ垂直的前提下,可以明确分界线为两者的中间位置。
Kernels(核)
1.核函数有多种,这里举的例子是高斯核函数
2.当取值点同landmark相近时,f值为1,;距离较远时,f值为0;
3.对于高斯核函数,σ2小时,核函数下降较快,大时,核函数下降较慢
SVM Parameters(SVM参数)
1.C:大时,相当于小lambda,低偏差,高方差;小时相当于大lambda,高偏差,低方差
2.σ2:大时,核函数平滑,下降慢,高偏差,低方差;小时,核函数陡峭,下降快,低偏差,高方差
SVM使用
1.求解一般直接使用封装好的库函数,极少自己求解,典型的库有liblinear和libsvm
2.具体调制的一般是C和核函数
3.核函数有许多种,一般用的时无核函数(线性核函数)和高斯核函数,其余还有多项式核函数以及其他
4.高斯核函数使用前必须对原始数据进行特征缩放处理
5.使用的核函数必须满足默赛尔定理
Multi‐class Classification(多类别分类)
2种方法:直接调用可函数和使用one vs. all方法