PCA主成份分析
一.PCA原理
主成分分析Principal Component Analysis,主要用途:数据的降维。可以理解为提取数据中更有价值的信息
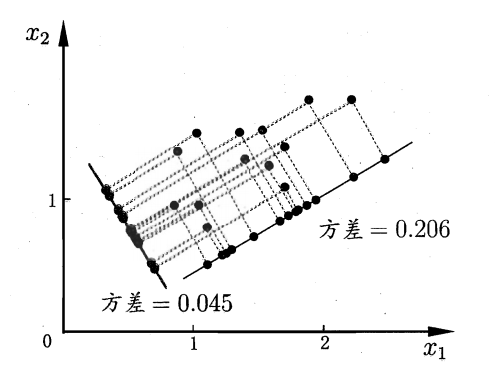
- 核心的思想:寻找一个新的坐标基,将原有的数据投影到新的坐标基中
1.1基本概念
-
样本均值
( x^-=frac{1}{n}sum^N_{i=1}x_i ) -
样本方差
( s^2=frac{1}{n-1}sum^n_{i=1}(x_i-x^-)^2 ) -
协方差
( Cov(X,Y)=frac{1}{n-1}sum^n_{i=1}(x_i-x^-)(y_i-y^-) ) -
协方差矩阵
假设有m个数据集,其中只有2个变量(特征),可以将数据表示为
[ X=
left[
egin{matrix}
a_1 & a_2 & cdots & a_m \
b_1 & b_2 & cdots & b_m \
end{matrix}
ight]
]
可以得到
[frac{1}{m}XX^T=
left[
egin{matrix}
frac{1}{m}sum^m_{i=1}a_i^2 & frac{1}{m}sum^m_{i=1}a_ib_i \
frac{1}{m}sum^m_{i=1}a_ib_i & frac{1}{m}sum^m_{i=1}b_i^2 \
end{matrix}
ight]
=
left[
egin{matrix}
Cov(a,a) & Cov(a,b) \
Cov(b,a) & Cov(b,b) \
end{matrix}
ight]
]
一般表示形式( 有d个特征值,协方差矩阵就是d*d )
[C=frac{1}{m}XX^T
]
另外,在numpy.cov中采用的是
[C=frac{1}{m-1}XX^T
]
因为最终我们需要计算的是协方差矩阵的特征向量,所以在上面的式子中m或者m-1不影响结果。
注意:上面的数据集中的X在进行协方差计算前需要进行去中心化处理,数据的均值为0
1.2计算步骤
- 去除平均值
- 计算协方差矩阵
- 计算协方差矩阵的特征值和特征向量
- 将特征值从大到小排序
- 保留最上面的N个特征向量
- 将数据转换到上述N个特征向量构建的新空间中
二.实例代码
2.1 实例1:简单数据

import numpy as np
data = np.mat([[-1,-1,0,2,0], [-2,0,0,1,1]]).T
# 计算协方差
## 方法1
cov_mat = np.cov(data, rowvar=0)
## 方法2
#mean_vec = np.mean(data, axis=0)
#print(mean_vec)
#cov_mat = (data - mean_vec).T.dot((data - mean_vec)) / (data.shape[0]-1)
#print('协方差矩阵
%s' %cov_mat)
# 计算特征值和特征向量
eig_als, eig_vecs = np.linalg.eig(cov_mat)
print('特征向量
%s' %eig_vecs)
print('
特征值
%s' %eig_vals)
# 投影到新的空间
new_vects = eig_vecs[:, 0]
new_data = data * new_vects
data:
matrix([[-1, -2],
[-1, 0],
[ 0, 0],
[ 2, 1],
[ 0, 1]])
cov_mat:
array([[1.5, 1. ],
[1. , 1.5]])
特征向量
[[ 0.70710678 -0.70710678]
[ 0.70710678 0.70710678]]
特征值
[2.5 0.5]
PCA降维后:
matrix([[-2.12132034],
[-0.70710678],
[ 0. ],
[ 2.12132034],
[ 0.70710678]])
2.2 实例2:莺尾花数据集
- 代码中是使用的数据集
链接:https://pan.baidu.com/s/1B-pgIzM-M-daPME8-14nQw
提取码:6abi
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
def plotData(dataX, dataY, stringX, stringY):
plt.figure(figsize=(6, 4))
for lab, col in zip(('Iris-setosa', 'Iris-versicolor', 'Iris-virginica'),
('blue', 'red', 'green')):
plt.scatter(dataX[dataY==lab, 0].tolist(),
dataX[dataY==lab, 1].tolist(),
label=lab, c=col)
plt.xlabel(stringX)
plt.ylabel(stringY)
plt.legend(loc='best')
plt.tight_layout()
plt.show()
# dataMat: 输入数据,每一行是一个样本
# topNfeat: 最终的维数
def pca(dataMat, topNfeat=9999999):
# 计算平均值,去中心化
meanVals = np.mean(dataMat, axis=0)
## 方法1
meanRemoved = dataMat - meanVals
## 方法2
# from sklearn.preprocessing import StandardScaler
# meanRemoved = StandardScaler().fit_transform(dataMat)
# 计算协方差
covMat = np.cov(meanRemoved, rowvar=0)
# 计算特征值和特征向量
eigVals,eigVects = np.linalg.eig(np.mat(covMat))
# 特征值排序
eigValInd = np.argsort(eigVals)
eigValInd = eigValInd[:-(topNfeat+1):-1]
redEigVects = eigVects[:,eigValInd]
# 映射出新的数据
lowDDataMat = meanRemoved * redEigVects
reconMat = (lowDDataMat * redEigVects.T) + meanVals
return lowDDataMat, reconMat
# 读取数据集
df = pd.read_csv('iris.data')
X = df.iloc[:,0:4].values
y = df.iloc[:,4].values
print(X.shape)
newX, recoMat = pca(X, 2)
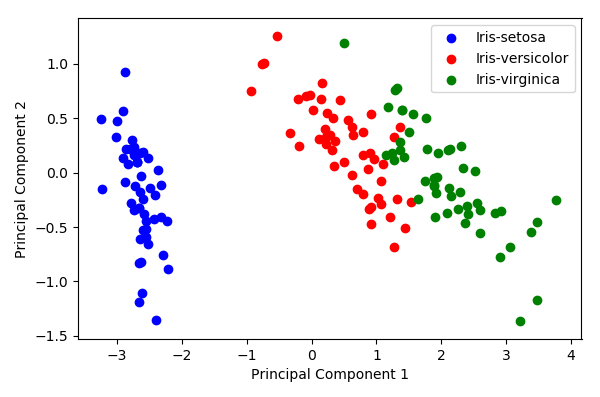
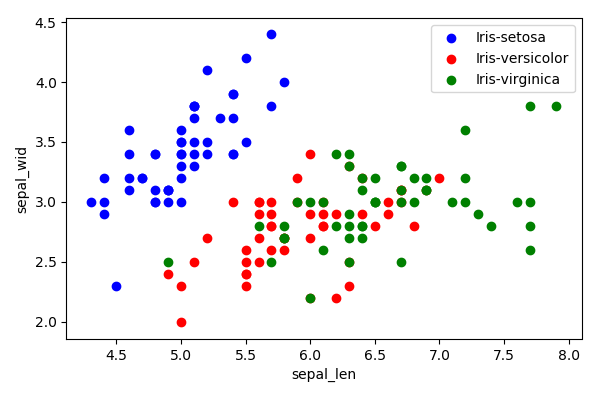
plotData(X, y, 'sepal_len', 'sepal_wid')
plotData(newX, y, 'Principal Component 1', 'Principal Component 2')
-
原始数据
-
PCA处理后