x的邻域基
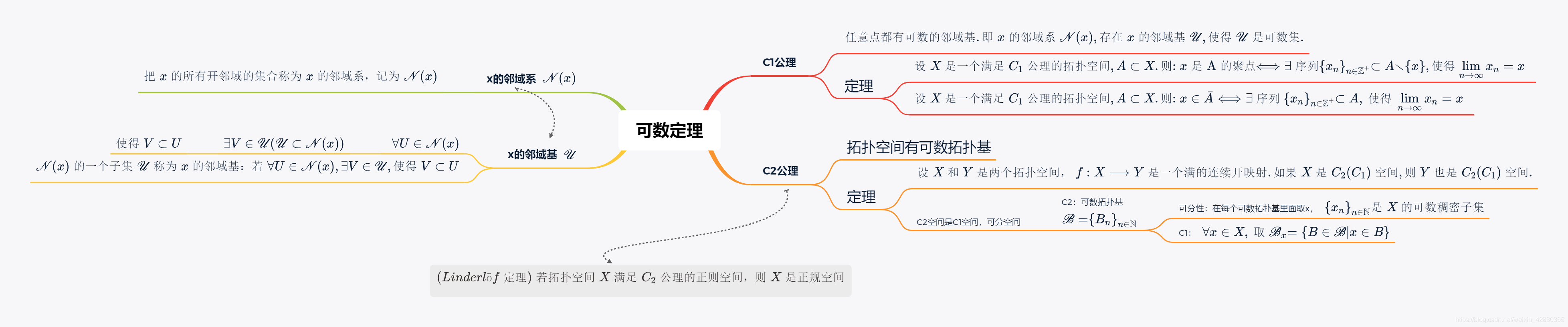
(mathscr{N}(x) 的一个子集 mathscr{U} 称为 x 的邻域基:若 forall U in mathscr{N}(x), 存 在 V in mathscr{U}, 使得 V subset U)
C1公理
任意点都有可数的邻域基.即 (x) 的邻域系 (mathscr{N}(x),) 存在 (x) 的邻域基 (mathscr{U},) 使得 (mathscr{U}) 是可数集
C2公理
C2:拓扑空间有可数拓扑基
C2空间是C1空间,可分空间
C2:定义可得可数集(mathscr{B}=left{B_{n}
ight}_{n in mathbb{N}})
可分性:
在每个可数拓扑基里面取(left{x_{n}
ight}_{n in mathbb{N}}) 是 (X) 的可数稠密子集
с1公理:
(forall x in X,) 取 (mathscr{B}_{x}={B in mathscr{B} | x in B})