线性滤波与卷积的基本概念
线性滤波可以说是图像处理最基本的方法,它可以允许我们对图像进行处理,产生很多不同的效果。做法很简单。首先,我们有一个二维的滤波器矩阵(有个高大上的名字叫卷积核)和一个要处理的二维图像。然后,对于图像的每一个像素点,计算它的邻域像素和滤波器矩阵的对应元素的乘积,然后加起来,作为该像素位置的值。这样就完成了滤波过程。

对图像和滤波矩阵进行逐个元素相乘再求和的操作就相当于将一个二维的函数移动到另一个二维函数的所有位置,这个操作就叫卷积或者协相关。卷积和协相关的差别是,卷积需要先对滤波矩阵进行180的翻转,但如果矩阵是对称的,那么两者就没有什么差别了。
Correlation 和 Convolution可以说是图像处理最基本的操作,但却非常有用。这两个操作有两个非常关键的特点:它们是线性的,而且具有平移不变性shift-invariant。平移不变性指我们在图像的每个位置都执行相同的操作。线性指这个操作是线性的,也就是我们用每个像素的邻域的线性组合来代替这个像素。这两个属性使得这个操作非常简单,因为线性操作是最简单的,然后在所有地方都做同样的操作就更简单了。
实际上,在信号处理领域,卷积有广泛的意义,而且有其严格的数学定义,但在这里不关注这个。
2D卷积需要4个嵌套循环4-double loop,所以它并不快,除非我们使用很小的卷积核。这里一般使用3x3或者5x5。而且,对于滤波器,也有一定的规则要求:
1)滤波器的大小应该是奇数,这样它才有一个中心,例如3x3,5x5或者7x7。有中心了,也有了半径的称呼,例如5x5大小的核的半径就是2。
2)滤波器矩阵所有的元素之和应该要等于1,这是为了保证滤波前后图像的亮度保持不变。当然了,这不是硬性要求了。
3)如果滤波器矩阵所有元素之和大于1,那么滤波后的图像就会比原图像更亮,反之,如果小于1,那么得到的图像就会变暗。如果和为0,图像不会变黑,但也会非常暗。
4)对于滤波后的结构,可能会出现负数或者大于255的数值。对这种情况,我们将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
神奇的卷积核
上面说到,对图像的滤波处理就是对图像应用一个小小的卷积核,那这个小小的卷积核到底有哪些魔法。下面我们一起来领略下一些简单但不简单的卷积核的魔法。
1、啥也不做
哈哈,大家可以看到啥了吗?这个滤波器啥也没有做,得到的图像和原图是一样的。因为只有中心点的值是1。邻域点的权值都是0,对滤波后的取值没有任何影响。
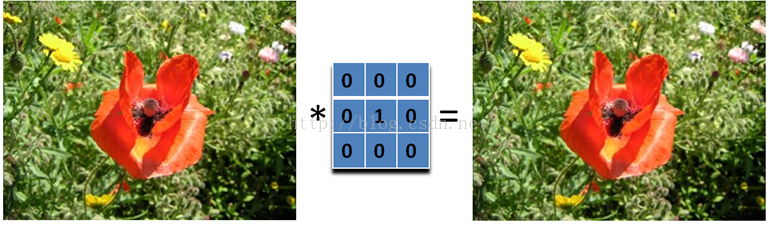
下面我们动点真格的。
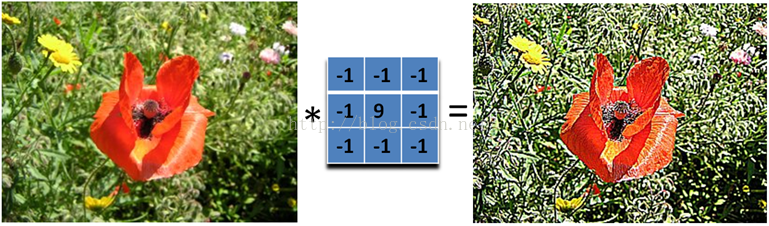
2、图像锐化滤波器Sharpness Filter
图像的锐化和边缘检测很像,首先找到边缘,然后把边缘加到原来的图像上面,这样就强化了图像的边缘,使图像看起来更加锐利了。这两者操作统一起来就是锐化滤波器了,也就是在边缘检测滤波器的基础上,再在中心的位置加1,这样滤波后的图像就会和原始的图像具有同样的亮度了,但是会更加锐利。
我们把核加大,就可以得到更加精细的锐化效果
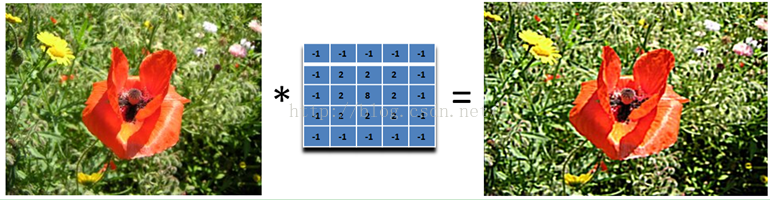
另外,下面的滤波器会更强调边缘:
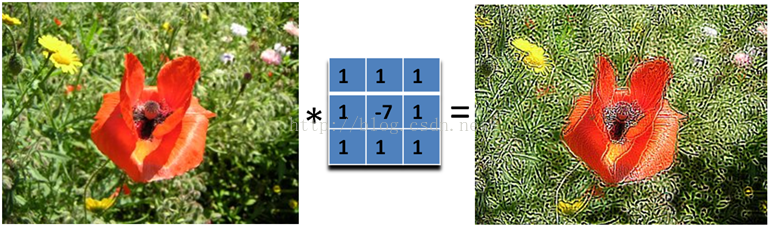
主要是强调图像的细节。最简单的3x3的锐化滤波器如下:
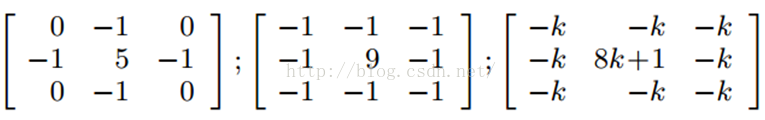
大家应该也看出来了,锐化滤波器实际上就是计算当前点和周围点的差别,然后将这个差别加到原来的位置上。
3、边缘检测Edge Detection
我们要找水平的边缘:需要注意的是,这里矩阵的元素和是0,所以滤波后的图像会很暗,只有边缘的地方是有亮度的。
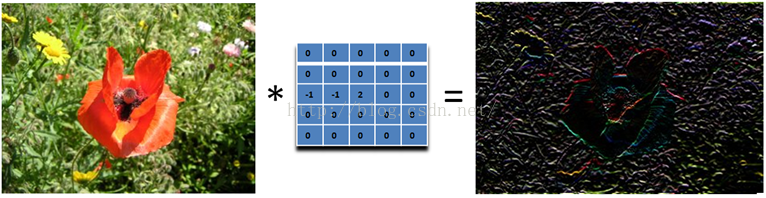
为什么这个滤波器可以寻找到水平边缘呢?因为用这个滤波器卷积相当于求导的离散版本:你将当前的像素值减去前一个像素值,这样你就可以得到这个函数在这两个位置的差别或者斜率。下面的滤波器可以找到垂直方向的边缘,这里像素上和下的像素值都使用:
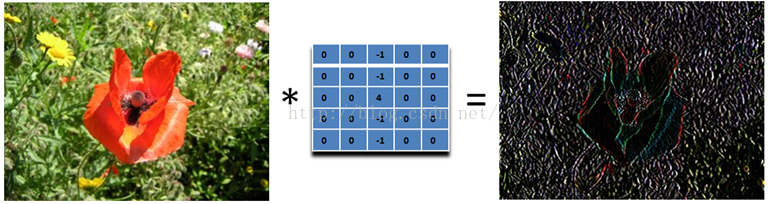
再下面这个滤波器可以找到45度的边缘:取-2不为了什么,只是为了让矩阵的元素和为0而已。
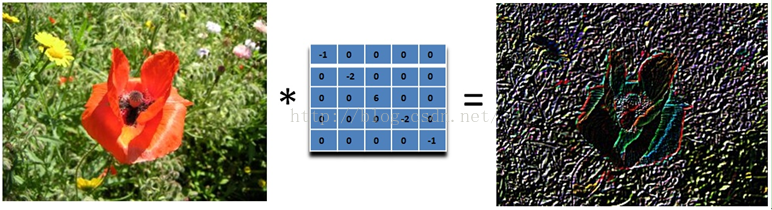
那下面这个滤波器就可以检测所有方向的边缘:
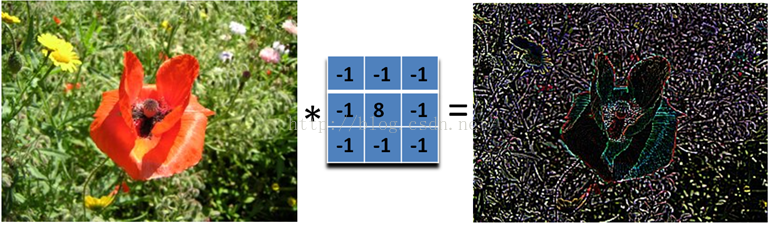
为了检测边缘,我们需要在图像对应的方向计算梯度。用下面的卷积核来卷积图像,就可以了。但在实际中,这种简单的方法会把噪声也放大了。另外,需要注意的是,矩阵所有的值加起来要是0.
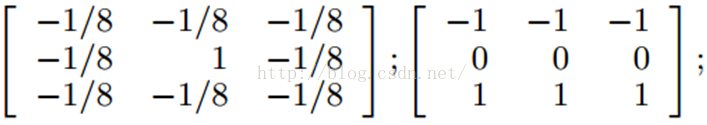
4、浮雕Embossing Filter
浮雕滤波器可以给图像一种3D阴影的效果。只要将中心一边的像素减去另一边的像素就可以了。这时候,像素值有可能是负数,我们将负数当成阴影,将正数当成光,然后我们对结果图像加上128的偏移。这时候,图像大部分就变成灰色了。
下面是45度的浮雕滤波器
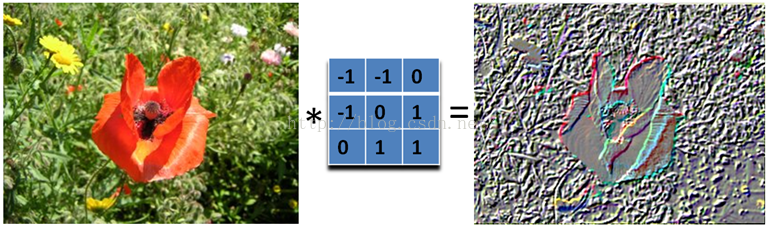
我们只要加大滤波器,就可以得到更加夸张的效果了
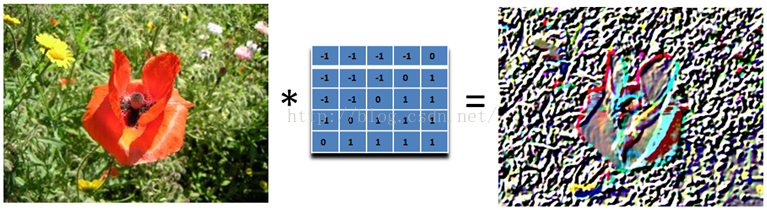
这种效果非常的漂亮,就像是将一副图像雕刻在一块石头上面一样,然后从一个方向照亮它。它和前面的滤波器不同,它是非对称的。另外,它会产生负数值,所以我们需要将结果偏移,以得到图像灰度的范围。


A:原图像。B:锐化。C:边缘检测。D:浮雕
5、运动模糊Motion Blur
运动模糊可以通过只在一个方向模糊达到,例如下面9x9的运动模糊滤波器。注意,求和结果要除以9。

这个效果就好像,摄像机是从左上角移动的右下角。
看了一些好玩的滤波器后我们来看均值模糊:
均值模糊Box Filter (Averaging)
我们可以将当前像素和它的四邻域的像素一起取平均,然后再除以5,或者直接在滤波器的5个地方取0.2的值即可,如下图:
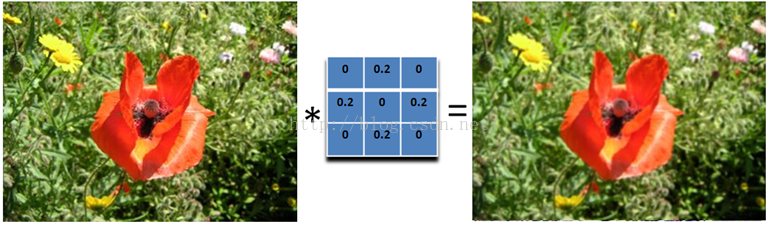
可以看到,这个模糊还是比较温柔的,我们可以把滤波器变大,这样就会变得粗暴了:注意要将和再除以13.
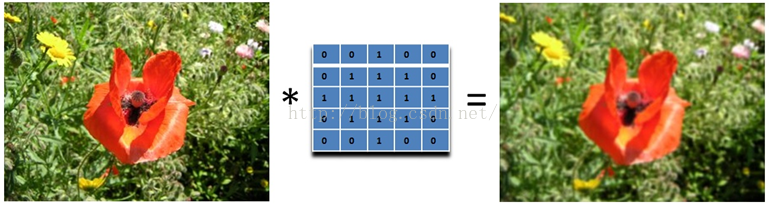
所以,如果你想要更模糊的效果,加大滤波器的大小即可。或者对图像应用多次模糊也可以。
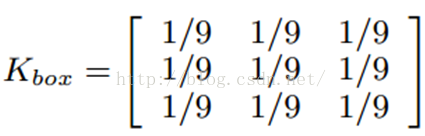

高斯模糊
其实模糊滤波器就是对周围像素进行加权平均处理,均值模糊很简单,周围像素的权值都相同,所以不是很平滑。高斯模糊就有这个优点,所以被广泛用在图像降噪上。特别是在边缘检测之前,都会用来移除细节。那么下面我们就看看高斯模糊的权值是如何分配的。

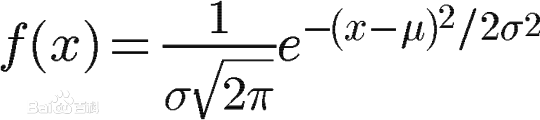
其中,μ是x的均值,σ是x的标准差。因为计算平均值的时候,中心点就是原点,所以μ等于0。即:

根据一维高斯函数,可以推导得到二维高斯函数:
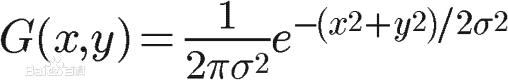
有了这个函数 ,就可以计算每个点的权重了。
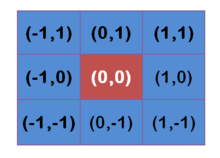
更远的点以此类推。下面就是5*5的高斯滤波器和平滑效果:
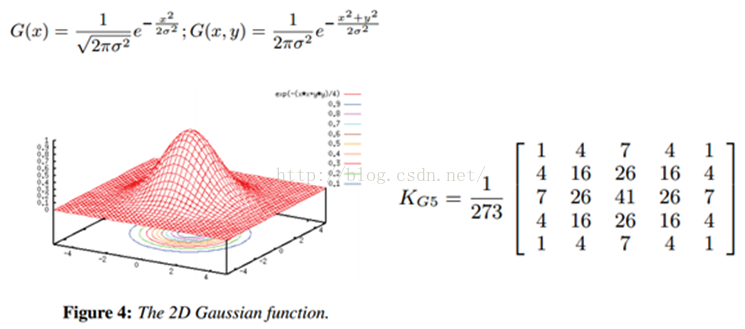

转自:https://www.cnblogs.com/magic8sky/p/6104377.html
