- 这里谈一下最小生成树
- 生成树的概念:连通图G的一个子图如果是一棵包含G的所有顶点的树,则该子图称为G的生成树。生成树是连通图的极小连通子图。所谓极小是指:若在树中任意增加一条边,则将出现一个回路;若去掉一条边,将会使之变成非连通图。 生成树各边的权值总和称为生成树的权。权最小的生成树称为最小生成树。
- 最小生成树一个有 n 个结点的连通图的生成树是原图的极小连通子图,且包含原图中的所有 n 个结点,并且有保持图连通的最少的边。常用于求最小生成树得算法包括kruskal(克鲁斯卡尔)算法或Prim(普里姆)算法。
- 最常用的是kruscal算法。kruscal算法的实质是用贪心策略来求得图的最小生成树。初始状态图中一条边也没有,每个点独立的存在于集合中;每次取出当前边权最小的边,判断能否将此边加入生成树中,判断依据:边的两个端点是否在一个集合中。若两点在一个集合中,则不需加入该边;若两点不在一个集合中,则将两点所在的集合合并,即集合中的点可以互相到达,无需两两之间再建边;如此做直到集合中各个点都联通或边全部枚举完毕;若此图联通,则为最小生成树。保证边权递增可以用快速排序的思想,维护集合关系可以用并查集的思想。排序复杂度O(eloge),枚举复杂度O(e),总体复杂度O(eloge)。
- 相比于kruscal算法,prim算法比较复杂;同样的是,prim算法也使用了贪心的策略,不过该算法是由点来贪心的。初始时边集u为空,点集v有一个点x,x为任意一点。操作步骤:在所有点中找到一点y,使d[y,r]最小,其中r∈v;把该边加入u,改点加入v,更新答案。如此做直到每个点都在点集中或某些点无法加入点集。若所有点都在点集中,则为最小生成树。枚举每个点加入集合,复杂度O(n),枚举该点与点集的距离,复杂度O(n),总体复杂度O(n2)。若用堆优化枚举距离的过程,复杂度降至O(nlogn)。
- 下面是关于最小生成树的几道杂题。
Problem 1 最小生成树
题目描述
如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出orz
输入输出格式
输入格式:
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式:
输出包含一个数,即最小生成树的各边的长度之和;如果该图不连通则输出orz
输入输出样例
4 5 1 2 2 1 3 2 1 4 3 2 3 4 3 4 3
7
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=20
对于40%的数据:N<=50,M<=2500
对于70%的数据:N<=500,M<=10000
对于100%的数据:N<=5000,M<=200000
样例解释:
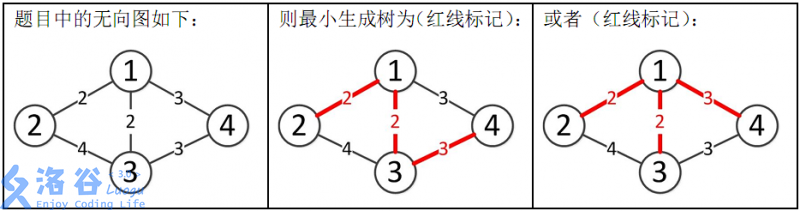
所以最小生成树的总边权为2+2+3=7
- 最小生成树模板题,由数据范围可知,kruscal算法即可。复杂度O(mlogm)。
1 #include <cstdio> 2 #include <iostream> 3 #include <algorithm> 4 using namespace std; 5 6 struct bian { 7 int x,y,a; 8 } e[200050]; 9 10 bool cmp(const bian p,const bian q){ 11 return p.a<q.a; 12 } 13 14 int n,m,ans,t,father[5050]; 15 16 int gf(int x) { 17 if (father[x]==x) return(x); 18 father[x]=gf(father[x]); 19 return(father[x]); 20 } 21 22 int main(){ 23 scanf("%d%d",&n,&m); 24 for (int i=1; i<=m; i++) scanf("%d%d%d",&e[i].x,&e[i].y,&e[i].a); 25 for (int i=1; i<=n; i++) father[i]=i; 26 sort(e+1,e+m+1,cmp); 27 for (int i=1; i<=m; i++) { 28 int fx=gf(e[i].x); 29 int fy=gf(e[i].y); 30 if (fx!=fy) { 31 father[fx]=fy; 32 ans+=e[i].a; 33 } 34 } 35 t=gf(1); 36 bool f=true; 37 for (int i=2; i<=n; i++) { 38 if (gf(i)!=t) { 39 printf("orz"); 40 f=0; 41 break; 42 } 43 } 44 if (f) printf("%d",ans); 45 return 0; 46 }
Problem 2 公路修建
题目描述
某国有n个城市,它们互相之间没有公路相通,因此交通十分不便。为解决这一“行路难”的问题,政府决定修建公路。修建公路的任务由各城市共同完成。
修建工程分若干轮完成。在每一轮中,每个城市选择一个与它最近的城市,申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。
政府审批的规则如下:
(1)如果两个或以上城市申请修建同一条公路,则让它们共同修建;
(2)如果三个或以上的城市申请修建的公路成环。如下图,A申请修建公路AB,B申请修建公路BC,C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请;

(3)其他情况的申请一律同意。
一轮修建结束后,可能会有若干城市可以通过公路直接或间接相连。这些可以互相:连通的城市即组成“城市联盟”。在下一轮修建中,每个“城市联盟”将被看作一个城市,发挥一个城市的作用。
当所有城市被组合成一个“城市联盟”时,修建工程也就完成了。
你的任务是根据城市的分布和前面讲到的规则,计算出将要修建的公路总长度。
输入输出格式
输入格式:
第一行一个整数n,表示城市的数量。(n≤5000)
以下n行,每行两个整数x和y,表示一个城市的坐标。(-1000000≤x,y≤1000000)
输出格式:
一个实数,四舍五入保留两位小数,表示公路总长。(保证有惟一解)
输入输出样例
4 0 0 1 2 -1 2 0 4
6.47
说明
修建的公路如图所示: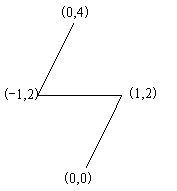
- 本题思路比较明确,即求出最小生成树即可。
- 数据范围,n≤5000。相当于5000*5000条边(kruscal已gg),那只能用prim了。
- 复杂度O(n2),应该是能通过的。
1 #include <cstdio> 2 #include <iostream> 3 #include <algorithm> 4 #include <cmath> 5 6 int n,x[5050],y[5050]; 7 double d[5050],ans; 8 bool v[5050]; 9 10 double cal(int a,int b) 11 { 12 double e1,e2; 13 e1=abs(x[a]-x[b]);e2=abs(y[a]-y[b]); 14 return sqrt(e1*e1+e2*e2); 15 } 16 17 int main() { 18 scanf("%d",&n); 19 for (int i=1; i<=n; i++) scanf("%d%d",&x[i],&y[i]); 20 for (int i=2; i<=n; i++) d[i]=cal(1,i); 21 d[1]=0; 22 v[1]=1; 23 for (int i=2; i<=n; i++) { 24 double minn=2147483647; 25 int cur=0; 26 for (int j=1; j<=n; j++) 27 if (!v[j] && d[j]<minn) { 28 minn=d[j]; 29 cur=j; 30 } 31 ans=ans+d[cur]; 32 v[cur]=1; 33 for (int j=1; j<=n; j++) if (!v[j] && d[j]>cal(cur,j)) d[j]=cal(cur,j); 34 } 35 printf("%.2lf",ans); 36 return 0; 37 }
Problem 3 清理仓库
题目描述
李老师的仓库已经有很多年没有清扫了,所以这次的计划是用河水来冲。仓库是一个N*M的矩形,且每个格子里都堆满了尘土。相邻的格子之间都有门,要想让水冲进去,就必须打开这些门。这可不是一件容易的事情。因为有些格子里土堆得很高,因此打开门就很费劲。推开(或拉开)一扇从A格子到B格子的门,需要的力度值为B房间里土堆的高度。写一个程序计算至少需要花费多少力气,才能使所有的格子都进水。
输入输出格式
输入格式:
第一行为N和M(N, M <= 40),代表仓库的大小。
以后N行,每行N个整数(每个数不超过100),分别表示每个格子里土堆的厚度。
输出格式:
你得到的结果。所有的格子必须都进水。水是从左上角的格子进去的。
输入输出样例
3 4 3 5 2 1 7 3 4 8 1 6 5 7
26
- 一道最小生成树建模的题。由题意,若要两个房间联通,需要打开中间的门,而开门只有两种方式,即推开和拉开,据此建边,求最小生成树即可。
- 时间复杂度O(n*m*4*log (n*m*4)),可以通过该题。
1 var 2 n,m,i,j,k,fx,fy,ans :longint; 3 father :array[0..2050] of longint; 4 a :array[0..2050] of longint; 5 l,r,w :array[0..10050] of longint; 6 7 procedure swap(var x,y:longint); 8 var 9 t :longint; 10 begin 11 t:=x; 12 x:=y; 13 y:=t; 14 end; 15 16 procedure sort(ll,rr:longint); 17 var 18 i,j,x :longint; 19 begin 20 i:=ll; j:=rr; x:=w[(ll+rr)>>1]; 21 while i<j do 22 begin 23 while w[i]<x do inc(i); 24 while w[j]>x do dec(j); 25 if i<=j then 26 begin 27 swap(w[i],w[j]); 28 swap(l[i],l[j]); 29 swap(r[i],r[j]); 30 inc(i); 31 dec(j); 32 end; 33 end; 34 if i<rr then sort(i,rr); 35 if j>ll then sort(ll,j); 36 end; 37 38 function min(x,y:longint):longint; 39 begin 40 if x<y then exit(x) else exit(y); 41 end; 42 43 function gf(x:longint):longint; 44 begin 45 if father[x]=x then exit(x); 46 father[x]:=gf(father[x]); 47 exit(father[x]); 48 end; 49 50 begin 51 read(n,m); 52 for i:=1 to n*m do read(a[i]); 53 for i:=1 to n*m do father[i]:=i; 54 for i:=1 to n*m do 55 begin 56 if i mod m<>0 then 57 begin 58 inc(k); 59 l[k]:=i; 60 r[k]:=i+1; 61 w[k]:=min(a[l[k]],a[r[k]]); 62 end; 63 if i<=(n-1)*m then 64 begin 65 inc(k); 66 l[k]:=i; 67 r[k]:=i+m; 68 w[k]:=min(a[l[k]],a[r[k]]); 69 end; 70 end; 71 sort(1,k); 72 for i:=1 to k do 73 begin 74 fx:=gf(l[i]); 75 fy:=gf(r[i]); 76 if fx<>fy then 77 begin 78 father[fx]:=fy; 79 inc(ans,w[i]); 80 end; 81 end; 82 writeln(ans); 83 end.
Problem 4 [NOIP2013] 货车运输
题目描述
A 国有 n 座城市,编号从 1 到 n,城市之间有 m 条双向道路。每一条道路对车辆都有重量限制,简称限重。现在有 q 辆货车在运输货物, 司机们想知道每辆车在不超过车辆限重的情况下,最多能运多重的货物。
输入输出格式
输入格式:
输入文件名为 truck.in。
输入文件第一行有两个用一个空格隔开的整数 n,m,表示 A 国有 n 座城市和 m 条道
路。 接下来 m 行每行 3 个整数 x、 y、 z,每两个整数之间用一个空格隔开,表示从 x 号城市到 y 号城市有一条限重为 z 的道路。意:x 不等于 y,两座城市之间可能有多条道路。
接下来一行有一个整数 q,表示有 q 辆货车需要运货。
接下来 q 行,每行两个整数 x、y,之间用一个空格隔开,表示一辆货车需要从 x 城市运输货物到 y 城市,注意:x 不等于 y。
输出格式:
输出文件名为 truck.out。
输出共有 q 行,每行一个整数,表示对于每一辆货车,它的最大载重是多少。如果货
车不能到达目的地,输出-1。
输入输出样例
4 3 1 2 4 2 3 3 3 1 1 3 1 3 1 4 1 3
3 -1 3
说明
对于 30%的数据,0 < n < 1,000,0 < m < 10,000,0 < q< 1,000; 对于 60%的数据,0 < n < 1,000,0 < m < 50,000,0 < q< 1,000; 对于 100%的数据,0 < n < 10,000,0 < m < 50,000,0 < q< 30,000,0 ≤ z ≤ 100,000。
- 由题意可知本题要求图中联通边尽量大,所以可以想到最大生成树。
- 首先可以用kruscal算法得到一颗最大生成树,接着要找出两点间连边最小边权的边。比较简单的想法:暴力的求出路径上边的最小值,但复杂度较高,不是理想的策略。我们可以用倍增的想法,维护两点的最近公共祖先(lca)以及它们到最近公共祖先之间的距离。该算法复杂度O(mlogm+qlogn),比较理想,可以通过本题。
1 type 2 rec =record 3 l,r,w :longint; 4 end; 5 6 var 7 n,m,i,j,x,y,z,q,fx,fy,root,l :longint; 8 e :array[0..100050] of rec; 9 pre,last,other,len,d :array[0..100050] of longint; 10 vis :Array[0..100050] of boolean; 11 father :array[0..100050] of longint; 12 anc :array[0..100050,0..30] of longint; 13 minn :Array[0..100050,0..30] of longint; 14 15 function min(x,y:longint):longint; 16 begin 17 if x<y then exit(x) else exit(y); 18 end; 19 20 procedure swap(var a,b:rec); 21 var 22 c :rec; 23 begin 24 c:=a; 25 a:=b; 26 b:=c; 27 end; 28 29 procedure sort(l,r:longint); 30 var 31 i,j,x :longint; 32 begin 33 i:=l; j:=r; x:=e[(l+r)>>1].w; 34 while i<j do 35 begin 36 while e[i].w<x do inc(i); 37 while e[j].w>x do dec(j); 38 if i<=j then 39 begin 40 swap(e[i],e[j]); 41 inc(i); 42 dec(j); 43 end; 44 end; 45 if i<r then sort(i,r); 46 if j>l then sort(l,j); 47 end; 48 49 function gf(x:longint):longint; 50 begin 51 if father[x]=x then exit(x); 52 father[x]:=gf(father[x]); 53 exit(father[x]); 54 end; 55 56 procedure add(u,v,r:longint); 57 begin 58 inc(l); 59 pre[l]:=last[u]; 60 last[u]:=l; 61 other[l]:=v; 62 len[l]:=r; 63 end; 64 65 procedure dfs(x:longint); 66 var 67 p,q :longint; 68 begin 69 p:=last[x]; 70 while p<>0 do 71 begin 72 q:=other[p]; 73 if (not vis[q]) then 74 begin 75 vis[q]:=true; 76 d[q]:=d[x]+1; 77 minn[q,0]:=len[p]; 78 anc[q,0]:=x; 79 dfs(q); 80 end; 81 p:=pre[p]; 82 end; 83 end; 84 85 procedure bz; 86 var 87 i,j :longint; 88 begin 89 for j:=1 to 25 do 90 for i:=1 to n do 91 begin 92 minn[i,j]:=min(minn[i,j-1],minn[anc[i,j-1],j-1]); 93 anc[i,j]:=anc[anc[i,j-1],j-1]; 94 end; 95 end; 96 97 function lca(u,v:longint):longint; 98 var 99 t,ans,i :longint; 100 begin 101 if d[u]<d[v] then 102 begin 103 t:=u; 104 u:=v; 105 v:=t; 106 end; 107 ans:=maxlongint; 108 for i:=25 downto 0 do 109 begin 110 if d[anc[u,i]]>=d[v] then 111 begin 112 ans:=min(ans,minn[u,i]); 113 u:=anc[u,i]; 114 end; 115 end; 116 if u=v then exit(ans); 117 for i:=25 downto 0 do 118 begin 119 if (anc[u,i]<>anc[v,i]) then 120 begin 121 ans:=min(ans,minn[u,i]); 122 ans:=min(ans,minn[v,i]); 123 u:=anc[u,i]; 124 v:=anc[v,i]; 125 end; 126 end; 127 ans:=min(ans,minn[u,0]); 128 ans:=min(ans,minn[v,0]); 129 exit(ans); 130 end; 131 132 begin 133 read(n,m); 134 for i:=1 to n do father[i]:=i; 135 for i:=1 to m do read(e[i].l,e[i].r,e[i].w); 136 sort(1,m); 137 for i:=m downto 1 do 138 begin 139 fx:=gf(e[i].l); 140 fy:=gf(e[i].r); 141 if (fx<>fy) then 142 begin 143 father[fx]:=fy; 144 add(e[i].l,e[i].r,e[i].w); 145 add(e[i].r,e[i].l,e[i].w); 146 root:=e[i].l; 147 end; 148 end; 149 d[root]:=1; 150 vis[root]:=true; 151 dfs(root); 152 bz; 153 {writeln(root); 154 for i:=1 to n do 155 begin 156 for j:=0 to 10 do write(anc[i,j]); 157 writeln; 158 end; 159 for i:=1 to n do writeln(d[i]);} 160 read(q); 161 for i:=1 to q do 162 begin 163 read(x,y); 164 if gf(x)<>gf(y) then writeln(-1) else writeln(lca(x,y)); 165 end; 166 end.