[NOIP2011] 聪明的质检员（二分答案）

题目描述

小T 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有 n 个矿石，从 1到n 逐一编号，每个矿石都有自己的重量 wi 以及价值vi 。检验矿产的流程是：

1 、给定m 个区间[Li,Ri]；

2 、选出一个参数 W；

3 、对于一个区间[Li,Ri]，计算矿石在这个区间上的检验值Yi：

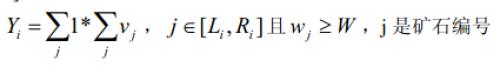
这批矿产的检验结果Y 为各个区间的检验值之和。即：Y1+Y2...+Ym

若这批矿产的检验结果与所给标准值S 相差太多，就需要再去检验另一批矿产。小T

不想费时间去检验另一批矿产，所以他想通过调整参数W 的值，让检验结果尽可能的靠近

标准值S，即使得S-Y 的绝对值最小。请你帮忙求出这个最小值。

输入输出格式

输入格式：

输入文件qc.in 。

第一行包含三个整数n，m，S，分别表示矿石的个数、区间的个数和标准值。

接下来的n 行，每行2个整数，中间用空格隔开，第i+1 行表示 i 号矿石的重量 wi 和价值vi。

接下来的m 行，表示区间，每行2 个整数，中间用空格隔开，第i+n+1 行表示区间[Li,Ri]的两个端点Li 和Ri。注意：不同区间可能重合或相互重叠

输出格式：

输出文件名为qc.out。

输出只有一行，包含一个整数，表示所求的最小值。

输入输出样例

输入样例#1：

5 3 15 
1 5 
2 5 
3 5 
4 5 
5 5 
1 5 
2 4 
3 3 

输出样例#1：

10

说明

【输入输出样例说明】

当W 选4 的时候，三个区间上检验值分别为 20、5 、0 ，这批矿产的检验结果为 25，此

时与标准值S 相差最小为10。

【数据范围】

对于10% 的数据，有 1 ≤n ，m≤10；

对于30% 的数据，有 1 ≤n ，m≤500 ；

对于50% 的数据，有 1 ≤n ，m≤5,000；

对于70% 的数据，有 1 ≤n ，m≤10,000 ；

对于100%的数据，有 1 ≤n ，m≤200,000，0 < wi, vi≤10^6，0 < S≤10^12，1 ≤Li ≤Ri ≤n 。

• NOIP2011 day2t2，不是很难
• 通过观察数据范围可知，本题要采用O(n)或O(nlogn)的算法，但O(n)显然不现实，所以要采用O(nlogn)的方法
• 既然已经确定了算法的时间复杂度范围，我们就会很容易想到二分答案的方法。
• 通过题意可知答案只与参数w有关，所以我们才用二分w的方法寻找最优答案。
• 二分的左右界分别为矿石的最小质量和最大质量（否则无意义）。
• 对于每个二分出的w，利用前缀和算出符合质量条件的矿石并记录这些矿石的价值和，生成这些矿石的检测结果。
• 利用结果更新答案：如果结果等于标准值则答案为0；若结果小于标准值则用两个数的差的绝对值更新答案，并二分左区间（因为结果随w单调递减），大于则同理。
• 要注意本题的数据范围，要开64位。
• 时间复杂度O((n+m)*log(wi_max))。
• 期望得分100分。

var
    n,m,i,j,k                                    :longint;
    s,l,r,ans,mid,p                                :int64;
    tot,sum,v,w                                    :Array[0..200050] of int64;
    ll,rr                                        :array[0..200050] of longint;
    
function find(ww:int64):int64;
var
    i,j                                            :longint;
    answ                                        :int64;
begin
    fillchar(tot,sizeof(tot),0);
    fillchar(sum,sizeof(sum),0);
    for i:=1 to n do
    begin
        if (w[i]>=ww) then
        begin
            tot[i]:=tot[i-1]+1;
            sum[i]:=sum[i-1]+v[i];
        end else
        begin
            tot[i]:=tot[i-1];
            sum[i]:=sum[i-1];
        end;
    end;
    answ:=0;
    for i:=1 to m do answ:=answ+(tot[rr[i]]-tot[ll[i]-1])*(sum[rr[i]]-sum[ll[i]-1]);
    exit(answ);
end;
    
begin
    read(n,m,s);
    l:=maxlongint;
    r:=0;
    for i:=1 to n do 
    begin
        read(w[i],v[i]);
        if w[i]<l then l:=w[i];
        if w[i]>r then r:=w[i];
    end;
    for i:=1 to m do read(ll[i],rr[i]);
    ans:=4000000000000000000;
    while (l<=r) do
    begin
        mid:=(l+r)>>1;
        p:=find(mid);
        if p=s then
        begin
            ans:=0;
            break;
        end;
        if (p<s) then
        begin
            if s-p<ans then ans:=s-p;
            r:=mid-1;
        end else
        begin
            if p-s<ans then ans:=p-s;
            l:=mid+1;
        end;
    end;
    writeln(ans);
end.