csp-s模拟测试90「光线追踪,临面合并」

光线追踪

30分暴力就是看每个光线和每个矩形的下边界和左边界交点

发现询问很难,

离线下来操作,

可以把角度离散化,转化为区间赋值,单点查询问题

每次就是给属于下边界角度内赋max,左边界角度内赋max

我突然感觉没什么可写的

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define A 5471745
struct node{
    ll ord,x;
    node(){}
    node(const ll &a,const ll &b){ord=a,x=b;}
};    
node Min(node a,node b){
    return a.x<b.x?a:a.x==b.x?(a.ord<b.ord?b:a):b;
}
ll pan(ll x){
    if(x>1e9) return 0;
    return x;
}
struct tree{
    node w[A];
    ll cl[A],cr[A];
    void built(ll x,ll l,ll r){
        cl[x]=l,cr[x]=r;
        w[x]=node(1e9+7,1e9+7);
        if(l==r){
            return ;
        }
        ll mid=(l+r)>>1;
        built(x<<1,l,mid);
        built(x<<1|1,mid+1,r);
    }
    void change(ll x,ll l,ll r,ll ord,ll val){
        if(cl[x]>=l&&cr[x]<=r){
//            printf("l=%lld r=%lld w[].val=%lld val=%lld
",cl[x],cr[x],w[x].x,val);
            w[x]=Min(w[x],node(ord,val));
            return ;
        }
        ll mid=(cl[x]+cr[x])>>1;
        if(mid>=l) change(x<<1,l,r,ord,val);
        if(mid<r) change(x<<1|1,l,r,ord,val);
    }
    node ask(ll x,ll pla){
        if(cl[x]==cr[x]) return w[x];
        node p;
        ll mid=(cl[x]+cr[x])>>1;
        if(mid>=pla) p=ask(x<<1,pla);
        else p=ask(x<<1|1,pla);
        return Min(p,w[x]);//标记永久化
    }
}X,Y;
ll x[A],xx[A],y[A],yy[A],opt[A];
ll mnx0=1e9+7,mnxid,mny0=1e9+7,mnyid,cnt,q;
long double lsh[A];
long double cl(ll x){
    if(x) return 1.0*x;
    return 1e-7L;
}
int main(){
    scanf("%lld",&q);
    for(ll i=1;i<=q;i++){
        scanf("%lld",&opt[i]);
        if(opt[i]==1){
            scanf("%lld%lld%lld%lld",&x[i],&y[i],&xx[i],&yy[i]);
            lsh[++cnt]=1.0L*y[i]/cl(x[i]),lsh[++cnt]=1.0L*yy[i]/cl(x[i]),lsh[++cnt]=1.0L*y[i]/cl(xx[i]);
        }
        else {
            scanf("%lld%lld",&x[i],&y[i]);
            if(x[i]) lsh[++cnt]=1.0L*y[i]/x[i];
        }
    }
    sort(lsh+1,lsh+cnt+1);
    ll len=unique(lsh+1,lsh+cnt+1)-lsh-1;
    X.built(1,1,len),Y.built(1,1,len);
    for(ll i=1;i<=q;i++){
        if(opt[i]==1){
            if(!x[i])if(mnx0>=y[i])mnx0=y[i],mnxid=i;
            if(!y[i])if(mny0>=x[i])mny0=x[i],mnyid=i;
            ll x1=lower_bound(lsh+1,lsh+len+1,1.0L*y[i]/cl(x[i]))-lsh;
            ll x3=lower_bound(lsh+1,lsh+len+1,1.0L*y[i]/cl(xx[i]))-lsh;
            ll x2=lower_bound(lsh+1,lsh+len+1,1.0L*yy[i]/cl(x[i]))-lsh;
//            printf("i=%lld
",i);
            X.change(1,x1,x2,i,x[i]),Y.change(1,x3,x1,i,y[i]);
        }
        else {
            if(!x[i]){printf("%lld
",mnxid);continue;}
            if(!y[i]){printf("%lld
",mnyid);continue;}
//            printf("i=%lld lower_bound(lsh+1,lsh+1+len,1.0L*y[i]/x[i])-lsh=%lld
",i,1ll*(lower_bound(lsh+1,lsh+1+len,1.0L*y[i]/x[i])-lsh));
            node a1=X.ask(1,lower_bound(lsh+1,lsh+1+len,1.0L*y[i]/x[i])-lsh),
              a2=Y.ask(1,lower_bound(lsh+1,lsh+1+len,1.0L*y[i]/x[i])-lsh);
            ll fx=a1.x,fy=a2.x;
//            printf("fx=%lld fy=%lld
",fx,fy);
            if(fx*y[i]==fy*x[i])printf("%lld
",pan(max(a1.ord,a2.ord)));
            else if(fx*y[i]<fy*x[i])printf("%lld
",pan(a1.ord));
            else printf("%lld
",pan(a2.ord));
        }
    }
}

临面合并

奇怪的数据范围应该给了一定的提示,8以内就基本是明示状压了

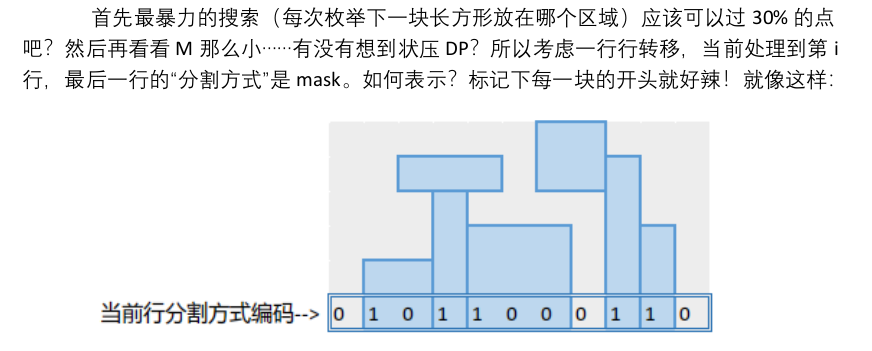
状态定义挺神的二进制下有一个1代表以当前点为右端点向左延伸出一个矩形

例如(假设原图是1 1 1 1)那么当前是0 1 0 1 表示两个矩形

判断一下是否可以与上面合并,减去相同贡献

过程可以预处理

不要用单调指针处理,单调指针细节特别多,

预处理

void fg(ll x){
    for(ll i=0;i<=maxn;i++){
        if((i&least[x])!=least[x]) continue ;
        if((i|maxx[x])!=maxx[x]) continue ;
        belong[x].push_back(i);
        ll cnt=0;
        for(ll j=1;j<=m;j++){
            if((i>>(j-1))&1)
                dl[++cnt]=j;
        }
        for(ll j=1;j<=cnt;j++){
            if(j==1) v[x][i].push_back(base[dl[1]]&a[x]);
            else v[x][i].push_back((base[dl[j]]^base[dl[j-1]])&a[x]);
        }
    }
}

减去相同贡献

                ll cnt=v[i][now].size();
                for(ll j1=0;j1<v[i][now].size();j1++)
                    for(ll j2=0;j2<v[i-1][last].size();j2++){
                        ll tox=v[i][now][j1],toy=v[i-1][last][j2];
                        if(tox==toy){
//                            printf("tox=%lld toy=%lld
",tox,toy);
                            cnt--;
                        }
                    }

 出题人题解