树上染色

树上染色

内存限制：256 MiB 时间限制：1000 ms 标准输入输出

 

 

题目描述

有一棵点数为 NNN 的树，树边有边权。给你一个在 0∼N0 sim N0∼N 之内的正整数 KKK，你要在这棵树中选择 KKK 个点，将其染成黑色，并将其他的 N−KN-KN−K 个点染成白色。将所有点染色后，你会获得黑点两两之间的距离加上白点两两之间距离的和的收益。

问收益最大值是多少。

输入格式

第一行两个整数 N,KN,KN,K。
接下来 N−1N-1N−1 行每行三个正整数 fr,to,dis ext{fr}, ext{to} , ext{dis}fr,to,dis，表示该树中存在一条长度为 dis ext{dis}dis 的边 (fr,to)( ext{fr}, ext{to})(fr,to)。
输入保证所有点之间是联通的。

输出格式

输出一个正整数，表示收益的最大值。

样例

样例输入

5 2
1 2 3
1 5 1
2 3 1
2 4 2

样例输出

17

样例解释

将点 1,21,21,2 染黑就能获得最大收益。

数据范围与提示

N≤2000, 0≤K≤NN leq 2000, 0 leq K leq NN≤2000, 0≤K≤N

第一次遇到这种题，我看了题解才过，觉得自己思维还有待提升

首先考虑f很好列但贡献特别难求难点就在于求贡献

设$f[x][j]$表示为以x为根时 给j个点染成黑色时最大值

我们轻易得到

$f[x][j]=max(f[x][j],f[x][j-w]+f[y][w]+val)$

注意这里f含义略微改变，我们把它当成背包一样转移

这是类似于一个子树合并的过程，假设当前枚举的是箭头指向的边

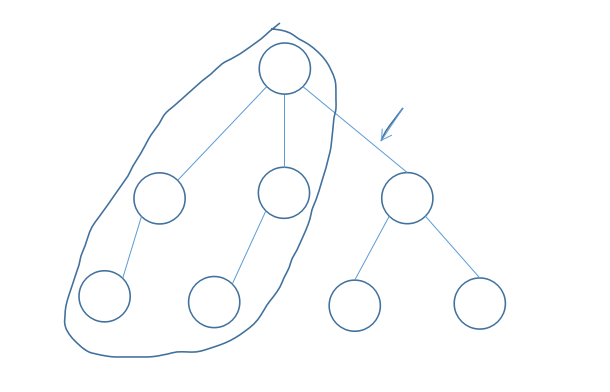
j-w是左边那一大堆，我们现在通过y这条边将子树合并过来使得最终状态为j

所以得到$f[x][j]=max(f[x][j],f[x][j-w]+f[y][w]+val)$

然后我们开始计算val

直接计算肯定不行，预处理也预处理不出来

然后我的思路就到这了，距离不是很好求

经过仔细思考（颓题解）

 发现其实我们要计算的val就是这条边的贡献

事实上这条边之外的点对是转移不过来的（图中圈中的相同颜色点对不用经过这条边）

那么我们就可以求出来这个边以下的黑点和y的兄弟为黑点构成的点对的贡献，

假设给y这个节点子树p个黑点，x兄弟共q-p个黑点

黑点之间贡献其实就是val*（p*（size[y]-p））

类似的，我们用容斥求出白点之间贡献最后得到

$(p*(k-p)+(size[y]-p)*(n-k-(size[y]-p)))*z$

转移就完了

你以为这是$n^3$的吗？

其实这有专门复杂度分析，具体可以查阅相关资料，大概是因为枚举点对之间贡献所以$n^2$

以下是本人丑陋的代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define A 6000
ll f[A][A],tot=0,deep[A],size[A],head[A],nxt[A],ver[A],edg[A],n,k;
bool flag[A];
void add(ll x,ll y,ll z){
    edg[++tot]=z,nxt[tot]=head[x],head[x]=tot,ver[tot]=y;
}
void dfs(ll x,ll pre){
    memset(f[x],-1,sizeof(f[x]));
    f[x][1]=f[x][0]=0;size[x]=1;
    for(ll i=head[x];i;i=nxt[i]){
        ll y=ver[i];
        if(y==pre) continue;
        dfs(y,x);
        size[x]+=size[y];
    }
    for(ll i=head[x];i;i=nxt[i]){
        ll y=ver[i],z=edg[i];
        if(y==pre) continue;
        for(ll q=min(k,size[x]);q>=0;q--)
            for(ll p=0;p<=min(q,size[y]);p++)
            if(q-p>=0&&f[x][q-p]!=-1)
            {
                ll val=(p*(k-p)+(size[y]-p)*(n-k-(size[y]-p)))*z;
//                printf("val=%lld x=%lld y=%lld q=%lld p=%lld
",val,x,y,q,p);
                f[x][q]=max(f[x][q],f[x][q-p]+f[y][p]+val);
            }
    }
}
int main(){
//    freopen("mkd.txt","r",stdin);
//    freopen("wa.txt","w",stdout);
    scanf("%lld%lld",&n,&k);
    for(ll i=1;i<=n-1;i++){
        ll xx,yy,zz;
        scanf("%lld%lld%lld",&xx,&yy,&zz);
        add(xx,yy,zz);add(yy,xx,zz);
    }
    dfs(1,0);
/*    for(ll i=1;i<=n;i++,puts(""))
        for(ll j=1;j<=k;j++){
            printf("f=%lld ",f[i][j]);
        }*/
    cout<<f[1][k]<<endl;
}