初识KMP（KMP模板 + KMP理论知识） hdu 1686

一，kmp 模板

前缀函数 即next函数

数组下标从0开始

void Prefix_Func()
 {
     int i,k;
     k=-1;
     next[0]=-1;
     for(i=1;i<m;i++)
     {
        while(k>=0 && P[k+1]!= P[i])
            k=next[k];
        if(P[k+1] == P[i])
            k++;
        next[i]=k;
     }
 }

匹配算法

 int Kmp()
 {
     int i,k;
     int cnt=0;
     k=-1;
     for(i=0;i<n;i++)
     {
        while(k>=0 && P[k+1]!= T[i])
            k=next[k];
        if(P[k+1] == T[i])
            k++;
        if(k == m-1)
        {
            //cnt++;
            k=next[k];
        }
     }
     //return cnt;
 }

二，理论介绍

模板 T，模式Pattern ，模式长度为m

关于模式的前缀函数；

1：模式P的前缀函数的定义，是函数∏：{1,2,……，m}→ {0,1,……，m-1}， 满足  ∏[q]=max{k:k<q 且 P_k ⊐ P_{q}。。。。。。。。。。。。可知 ∏[q] < q} 

_{2： w ⊐ x,w是x的后缀  ，w ⊏ x ， w是x的前缀。  符号⊏  ，竖线指向是头}

3： 定义： ∏^{*_{[q]= {∏[q] ,}}  ∏^{(2)_{[q] ,  ∏(3)[q],……，  ∏(t)[q]}   ,其中 ∏(i)[q]是按函数的迭代的概念来定义的，满足  ∏(0)[q]=q，并且对i≥ 1 ， ∏(i)[q]= ∏[ ∏(i-1)[q] ], 当达到 ∏(t)[q] =0 时，序列终止。}}

4：引理1

∏^{*_{[q]  =  {k: k<q 且  Pk ⊐ Pq}}}

5:引理2

如果  ∏[q] >0 ， 则  ∏[q]  - 1  ∈   ∏^*_[q-1]

6： 定义子集 E_q-1 = {k:k∈  ∏^{*_{[q-1],且 P[k+1] = P[q]}} }   = {k: k<q-1, P_k+1 ^⊐Pq }  

其中     ∏^{*_{[q-1]=    {∏[q-1] ,  ∏(2)[q-1] ,  ∏(3)[q-1],……，  ∏(t)[q-1]}}}   

7： 推论1

对q = 2 ,3,...,m      有 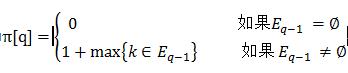   ， ∏[1]  = 0 ，因为要求∏[q] < q。

前缀函数的伪代码：

COMPUTE=PREFIX-FUNCTION(P)

 　　m=P.length

　　let  ∏[1,...,m] be a bew array

　　∏[1]=0       

　　k=0                                                 

　　for q 2 to m

　　　　while k>0 and P[k+1]‡P[q]

　　　　　　　　k=∏[k]

　　　　if P[k+1]==P[q]

　　　　　　　　k=k+1

　　　　∏[q] = k

 分析：

1:for 循环每次迭代开始时，k= ∏[q-1] ,初始 时，  ∏[1]=0 故令k=0

while 循环搜索所有 k∈  ∏*[q-1] ，直到找到一个k,使得  P[k+1]==P[q] ，此时的k也是满足条件的最大的。k是集合Eq-1 中的最大值， 然后设置 ∏[q]  = k+1 ,由推论可知。

2，这也算是一个递推，首项 ∏[1]=0  ，然后 由公式 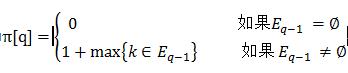       递推。

三，  kmp算法

---

用字符串匹配自动机来比喻说明：

字符串匹配自动机 M =（Q,q₀  ,A, Σ , δ） 五元组。

Q 是状态的 集合  {0 ，1 ，..., m} 

q_{0  表示初始状态   q0  = 0}

A 是一个特殊的接受状态集合   此时的 A= {m}

Σ   模板和模式  的元素都是来自 字母集 Σ

δ  转移函数  δ（q, a）= σ(P_q a)  

其中 ，q 是表示读完T_i 之后，自动机所处状态， 也是表示 P的前缀和T_i 后缀的最长匹配长度。

---

 kmp 算法伪代码

KMP-MATCHER(T ,P)
　　n=T.length
　　m=P.length
　　COMPUTER-PREFIX-FUNCTION(P) // 计算模式的前缀函数
　　k=0
　　for i=1 to n
　　　　　　while k>0 and P[k+1] != T[i] //搜索所有k'  ∈ ∏^{*_{[k]   , 找出满足  P[k+1] == T[i]  的最大的前缀k,然后继续匹配， 否则 k走到状态0}} 
　　　　　　　　k=∏[k]
　　　　　　if P[k+1] == T[i]
　　　　　　　　k=k+1
　　　　　　if k==m        状态k ==m  字符被接受
　　　　　　　　printf""
　　　　　　　　q=∏[q] // 避免在找到P的一次后，出现 P[m+1]错误，所以需要计算m的前缀

k表示自动机的状态，读完T_i 之后，自动机所处状态， 也是表示 P的前缀和T_i 后缀的最长匹配长度。  

状态转移公式 %%%%%%%%%%%%%%%%

   if  P[k + 1] = T'[i]     k' = k + 1  

 if  P[k + 1] != T'[i]        字符不能继续匹配，   这时我们必须找到一个更小的字串   k'   ∈ ∏^{*_{[k]  ,满足P[k + 1] = T'[i]      ，就停在k'这个状态，进行P[k' + 1] = T'[i]  匹配， 不然， k状态走完变成0 .}}

hdu  1686 代码

#include<iostream>
#include<stdio.h>
#include<string>
#include<string.h>
#define N 1000005  //模板长度
#define M 10005  //模式长度
using namespace std;
char T[N];      //
char P[M];     //
int next[M];     // 前缀函数值 next = pi
int n,m;

//求前缀函数
 void Prefix_Func()
 {
     int i,k;   
     k=-1;                  //下标从 0开始 的 ， 故 k = -1  满足 next[k]<k   ,循环第一次是i= 1 ，故满足 next[0]  = -1
     next[0]=-1;
     for(i=1;i<m;i++)  //    for循环入口条件是 next[i-1] = k 
     {
        while(k>=0 && P[k+1]!= P[i])        //证明过的函数 循环体内，要么就是找到 k  满足 P[k+1] = P[i] ，要么就是走到了 状态 -1 
            k=next[k];
        if(P[k+1] == P[i])    
            k++;
        next[i]=k;
     }
 }
 int Kmp()
 {
     int i,k;
     int cnt=0;
     k=-1;   // 初始状态为 -1 
     for(i=0;i<n;i++)
     {
        while(k>=0 && P[k+1]!= T[i])     // 状态转移公式     循环结束 k=-1 或者 P[k+1] = =  T[i]
            k=next[k];
        if(P[k+1] == T[i])
            k++;
        if(k == m-1)
        {
            cnt++;
            //k=next[k];
        }
     }
     return cnt;
 }
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        scanf("%s",P);
        scanf("%s",T);
        n=strlen(T);
        m=strlen(P);
        Prefix_Func();
        printf("%d
",Kmp());
    }
    return 0 ;
}