[NOI Online #2 提高组]涂色游戏

description:

solution:

不妨设(p_1le p_2)
首先(lcm(p_1,p_2))一定会成为一个循环节，于是我们只用考虑一个循环节的情况就可以了
那么最坏的情况就是对于某个正整数(m),([m*p_2+1,(m+1)*p_2-1])中间有最多的(p_1)的倍数

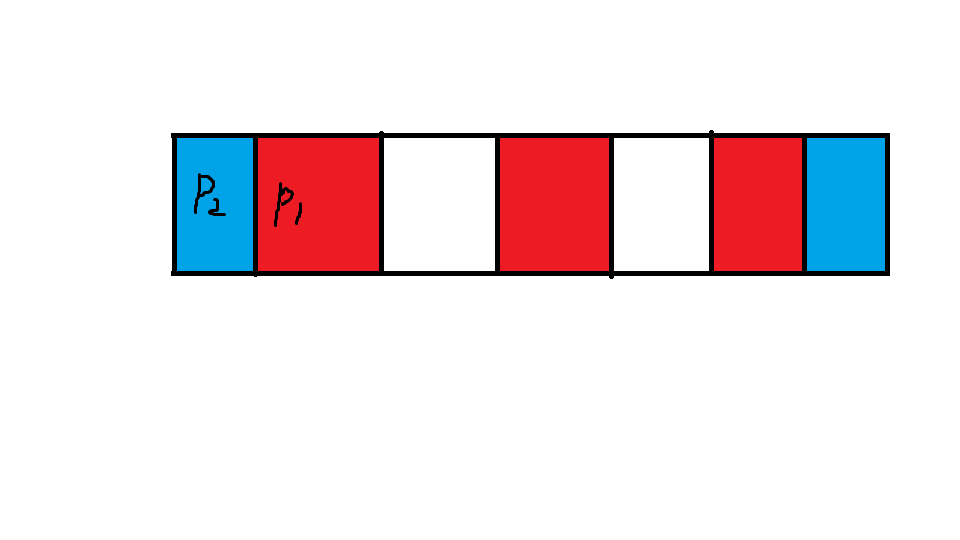
（这个图仅仅是为了方便理解，真正的情况下是不会出现这种情况的（毕竟这是(p1=2,p2=6)的情况啊,为什么会交错呢））
那么我们考虑最小化(n*p_1-m*p_2其中m,nin Z^*),因为这样我们就可以在([m*p_2+1,(m+1)*p_2-1])放下尽量多的(p_1)的倍数
根据裴蜀定理，(min(n*p_1-m*p_2)=gcd(p_1,p_2))
于是我们就可以快速计算出这个位置，然后判断最多放多少个(p_1)的倍数，最后再和(k)比较就行了
不过似乎要特判(p_1==p_2==k==1)的情况，不判断好像可以直接挂成20分（好数据）

code:

#include<bits/stdc++.h>
using namespace std;
int t;
int p1,p2,k;
int gcd(int a,int b){return !b?a:gcd(b,a%b);}
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d%d%d",&p1,&p2,&k);
		if(k==1){puts("No");continue;}
		int g=gcd(p1,p2);
		if(p1>p2)swap(p1,p2);
		if((p2-1-g)/p1+1<k)puts("Yes");
		else puts("No");
	}
	return 0;
}