A. Inscribed Figures
The math faculty of Berland State University has suffered the sudden drop in the math skills of enrolling students. This year the highest grade on the entrance math test was 8. Out of 100! Thus, the decision was made to make the test easier.
Future students will be asked just a single question. They are given a sequence of integer numbers a1,a2,…,ana1,a2,…,an, each number is from 11to 33 and ai≠ai+1ai≠ai+1 for each valid ii. The ii-th number represents a type of the ii-th figure:
- circle;
- isosceles triangle with the length of height equal to the length of base;
- square.
The figures of the given sequence are placed somewhere on a Cartesian plane in such a way that:
- (i+1)(i+1)-th figure is inscribed into the ii-th one;
- each triangle base is parallel to OX;
- the triangle is oriented in such a way that the vertex opposite to its base is at the top;
- each square sides are parallel to the axes;
- for each ii from 22 to nn figure ii has the maximum possible length of side for triangle and square and maximum radius for circle.
Note that the construction is unique for some fixed position and size of just the first figure.
The task is to calculate the number of distinct points (not necessarily with integer coordinates) where figures touch. The trick is, however, that the number is sometimes infinite. But that won't make the task difficult for you, will it?
So can you pass the math test and enroll into Berland State University?
The first line contains a single integer nn (2≤n≤1002≤n≤100) — the number of figures.
The second line contains nn integer numbers a1,a2,…,ana1,a2,…,an (1≤ai≤31≤ai≤3, ai≠ai+1ai≠ai+1) — types of the figures.
The first line should contain either the word "Infinite" if the number of distinct points where figures touch is infinite or "Finite" otherwise.
If the number is finite than print it in the second line. It's guaranteed that the number fits into 32-bit integer type.
3 2 1 3
Finite 7
3 1 2 3
Infinite
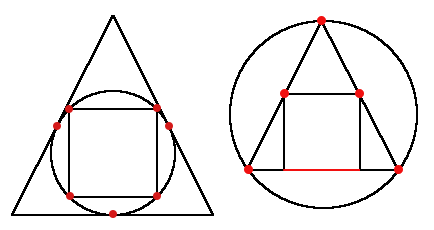
Here are the glorious pictures for the examples. Note that the triangle is not equilateral but just isosceles with the length of height equal to the length of base. Thus it fits into a square in a unique way.
The distinct points where figures touch are marked red.
In the second example the triangle and the square touch each other for the whole segment, it contains infinite number of points.
代码:

#include <bits/stdc++.h> using namespace std; const int maxn = 1e3 + 10; int N; int a[maxn]; int num[4]; void init() { num[1] = 9; num[2] = 3; num[3] = 4; } int main() { scanf("%d", &N); bool flag = true; for(int i = 0; i < N; i ++) { scanf("%d", &a[i]); if(i > 0) { if((a[i] == 3 && a[i - 1] == 2) || (a[i] == 2 && a[i - 1] == 3)) flag = false; } } if(!flag) printf("Infinite "); else { init(); int ans = 0; for(int i = 1; i < N; i ++) { ans += min(num[a[i]], num[a[i - 1]]); if(a[i - 1] == 3 && a[i] == 1 && a[i + 1] == 2) ans --; } printf("Finite %d ", ans); } return 0; }
B. Ugly Pairs
You are given a string, consisting of lowercase Latin letters.
A pair of neighbouring letters in a string is considered ugly if these letters are also neighbouring in a alphabet. For example, string "abaca" contains ugly pairs at positions (1,2)(1,2) — "ab" and (2,3)(2,3) — "ba". Letters 'a' and 'z' aren't considered neighbouring in a alphabet.
Can you rearrange the letters of a given string so that there are no ugly pairs? You can choose any order of the letters of the given string but you can't add any new letters or remove the existing ones. You can also leave the order the same.
If there are multiple answers, print any of them.
You also have to answer TT separate queries.
The first line contains a single integer TT (1≤T≤1001≤T≤100) — the number of queries.
Each of the next TT lines contains string ss (1≤|s|≤100)(1≤|s|≤100) — the string for the next query. It is guaranteed that it contains only lowercase Latin letters.
Note that in hacks you have to set T=1T=1.
Print TT lines. The ii-th line should contain the answer to the ii-th query.
If the answer for the ii-th query exists, then print such a rearrangment of letters of the given string that it contains no ugly pairs. You can choose any order of the letters of the given string but you can't add any new letters or remove the existing ones. You can also leave the order the same.
If there are multiple answers, print any of them.
Otherwise print "No answer" for that query.
4 abcd gg codeforces abaca
cadb gg codfoerces No answer
In the first example answer "bdac" is also correct.
The second example showcases the fact that only neighbouring in alphabet letters are not allowed. The same letter is ok.
There are lots of valid answers for the third example.
代码:

#include <bits/stdc++.h> using namespace std; int T; int num[30]; int main() { scanf("%d", &T); getchar(); while(T --) { memset(num, 0, sizeof(num)); string s; cin >> s; int len = s.length(); for(int i = 0; i < len; i ++) num[s[i] - 'a'] ++; string t = "", p = "", ans1 = "", ans2 = ""; for(int i = 0; i < 26; i ++) { if(num[i] == 0) continue; if(i % 2 == 0) { for(int it = 0; it < num[i]; it ++) t += ('a' + i); } else { for(int it = 0; it < num[i]; it ++) p += (i + 'a'); } } ans1 = p + t; ans2 = t + p; bool flag1 = true, flag2 = true; for(int i = 1; ans1[i]; i ++) if(abs(ans1[i] - ans1[i - 1]) == 1) flag1 = false; for(int i = 1; ans2[i]; i ++) if(abs(ans2[i] - ans2[i - 1]) == 1) flag2 = false; if(!flag1 && !flag2) printf("No answer "); else { if(flag1) cout << ans1 << endl; else cout << ans2 << endl; } } return 0; }
C. Match Points
You are given a set of points x1x1, x2x2, ..., xnxn on the number line.
Two points ii and jj can be matched with each other if the following conditions hold:
- neither ii nor jj is matched with any other point;
- |xi−xj|≥z|xi−xj|≥z.
What is the maximum number of pairs of points you can match with each other?
The first line contains two integers nn and zz (2≤n≤2⋅1052≤n≤2⋅105, 1≤z≤1091≤z≤109) — the number of points and the constraint on the distance between matched points, respectively.
The second line contains nn integers x1x1, x2x2, ..., xnxn (1≤xi≤1091≤xi≤109).
Print one integer — the maximum number of pairs of points you can match with each other.
4 2 1 3 3 7
2
5 5 10 9 5 8 7
1
In the first example, you may match point 11 with point 22 (|3−1|≥2|3−1|≥2), and point 33 with point 44 (|7−3|≥2|7−3|≥2).
In the second example, you may match point 11 with point 33 (|5−10|≥5|5−10|≥5).
代码:

#include <bits/stdc++.h> using namespace std; const int maxn = 2e5 + 10; int N, Z; int a[maxn]; map<int, int> mp; bool check(int x) { for(int i = 0; i < x; i ++) if(a[i] + Z > a[N - x + i]) return false; return true; } int main() { scanf("%d%d", &N, &Z); for(int i = 0; i < N; i ++) scanf("%d", &a[i]); sort(a, a + N); int l = 0, r = N / 2, mid, p = 0; while(l <= r) { mid = (l + r) / 2; if(check(mid)) { l = mid + 1; p = mid; } else r = mid - 1; } printf("%d ", p); return 0; }
明天上班今天就不想写题 厌学了 综艺两小时编码五分钟
