The following problem is well-known: given integers n and m, calculate
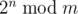 ,
,where 2n = 2·2·...·2 (n factors), and 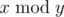 denotes the remainder of division of x by y.
denotes the remainder of division of x by y.
You are asked to solve the "reverse" problem. Given integers n and m, calculate
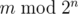 .
.The first line contains a single integer n (1 ≤ n ≤ 108).
The second line contains a single integer m (1 ≤ m ≤ 108).
Output a single integer — the value of 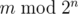 .
.
4
42
10
1
58
0
98765432
23456789
23456789
In the first example, the remainder of division of 42 by 24 = 16 is equal to 10.
In the second example, 58 is divisible by 21 = 2 without remainder, and the answer is 0.
特判一下,
然后就直接模了;
1 #include <iostream> 2 #define ll long long int 3 using namespace std; 4 ll n,m; 5 6 int main(){ 7 cin>>n>>m; 8 ll sum = 1; 9 if(n>=27){ 10 cout<<m<<endl; 11 }else{ 12 while(n--){ 13 sum*=2; 14 } 15 cout<<m%sum<<endl; 16 } 17 return 0; 18 }
Consider a rooted tree. A rooted tree has one special vertex called the root. All edges are directed from the root. Vertex u is called a child of vertex v and vertex v is called a parent of vertex u if there exists a directed edge from v to u. A vertex is called a leaf if it doesn't have children and has a parent.
Let's call a rooted tree a spruce if its every non-leaf vertex has at least 3 leaf children. You are given a rooted tree, check whether it's a spruce.
The definition of a rooted tree can be found here.
The first line contains one integer n — the number of vertices in the tree (3 ≤ n ≤ 1 000). Each of the next n - 1 lines contains one integer pi (1 ≤ i ≤ n - 1) — the index of the parent of the i + 1-th vertex (1 ≤ pi ≤ i).
Vertex 1 is the root. It's guaranteed that the root has at least 2 children.
Print "Yes" if the tree is a spruce and "No" otherwise.
4
1
1
1
Yes
7
1
1
1
2
2
2
No
8
1
1
1
1
3
3
3
Yes
The first example:
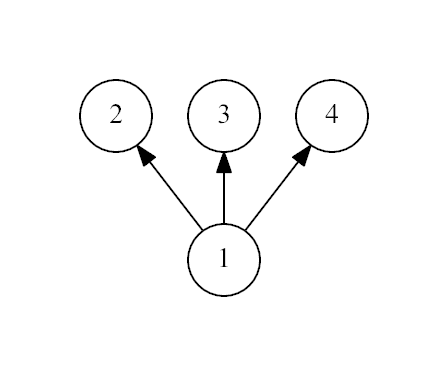
The second example:

It is not a spruce, because the non-leaf vertex 1 has only 2 leaf children.
The third example:
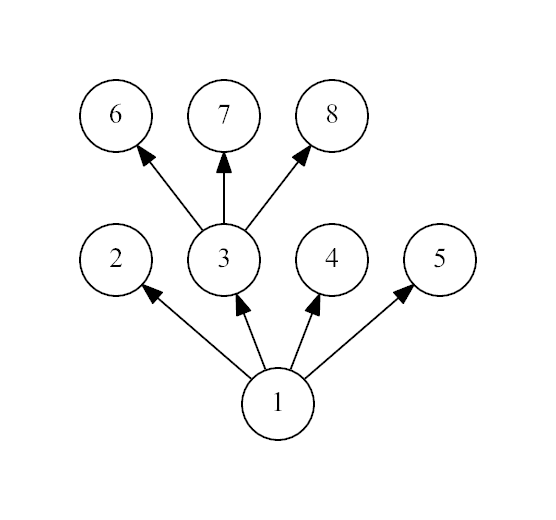
这题就判断了,多开几个数组标记就行,如果不是叶子,那么它就一定要有三个或以上的叶子。
1 #include <iostream> 2 using namespace std; 3 int n; 4 int k[1010]; 5 int ans[1010]; 6 int vis[1010]; 7 int main(){ 8 cin>>n; 9 for(int i=2;i<=n;i++){ 10 cin>>k[i]; 11 ans[k[i]] = 1; 12 } 13 for(int i=n;i>=2;i--){ 14 if(vis[i]==0){ 15 vis[k[i]]++; 16 } 17 } 18 for(int i=1;i<=n;i++){ 19 if(vis[i]<3&&vis[i]!=0){ 20 cout<<"No"<<endl; 21 return 0; 22 }else if(ans[i]&&vis[i]<3){ 23 cout<<"No"<<endl; 24 return 0; 25 } 26 } 27 cout<<"Yes"<<endl; 28 return 0; 29 }
A New Year party is not a New Year party without lemonade! As usual, you are expecting a lot of guests, and buying lemonade has already become a pleasant necessity.
Your favorite store sells lemonade in bottles of n different volumes at different costs. A single bottle of type i has volume 2i - 1 liters and costs ci roubles. The number of bottles of each type in the store can be considered infinite.
You want to buy at least L liters of lemonade. How many roubles do you have to spend?
The first line contains two integers n and L (1 ≤ n ≤ 30; 1 ≤ L ≤ 109) — the number of types of bottles in the store and the required amount of lemonade in liters, respectively.
The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 109) — the costs of bottles of different types.
Output a single integer — the smallest number of roubles you have to pay in order to buy at least L liters of lemonade.
4 12
20 30 70 90
150
4 3
10000 1000 100 10
10
4 3
10 100 1000 10000
30
5 787787787
123456789 234567890 345678901 456789012 987654321
44981600785557577
In the first example you should buy one 8-liter bottle for 90 roubles and two 2-liter bottles for 30 roubles each. In total you'll get 12 liters of lemonade for just 150 roubles.
In the second example, even though you need only 3 liters, it's cheaper to buy a single 8-liter bottle for 10 roubles.
In the third example it's best to buy three 1-liter bottles for 10 roubles each, getting three liters for 30 roubles.
这题看大佬的代码都是dp,dp,dp, 还有用二进制的,表示不懂,
所以就自己一直找bug,终于写出来了自己的思路的代码。
算是暴力过吧,思想就是找k[i]/list[i]最小的。特别要注意余数。
1 #include <bits/stdc++.h> 2 #define ll long long int 3 #define inf 1000000000000000000 4 using namespace std; 5 ll n,m; 6 ll k[35]; 7 ll List[35]; 8 double vis[35]; 9 double an[35]; 10 int main(){ 11 cin>>n>>m; 12 for(int i=0;i<n;i++){ 13 cin>>k[i]; 14 } 15 ll sum=1; 16 for(int i=0;i<n;i++){ 17 vis[i] = k[i]*1.0/sum*1.0; 18 an[i] = vis[i]; 19 List[i] = sum; 20 sum*=2; 21 } 22 sort(an,an+n); 23 ll cnt=0; 24 ll ans = inf; 25 ll nt = inf; 26 for(int i=0;i<n;i++){ 27 for(int j=0;j<n;j++){ 28 if(vis[j]==an[i]){ 29 if(List[j]<=m){ 30 ll x = (m/List[j])*k[j]; 31 ll y = m/List[j]; 32 if(x>=nt*(List[j]*1.0*y/m)){ 33 cnt+=nt; 34 m = 0; 35 }else{ 36 cnt+=x; 37 m = m%List[j]; 38 } 39 ans = min(cnt+k[j],ans),nt = min(k[j],nt); 40 break; 41 } 42 ans = min(cnt+k[j],ans),nt = min(k[j],nt); 43 break; 44 } 45 } 46 if(!m) 47 break; 48 } 49 cnt = min(ans,cnt); 50 cout<<cnt<<endl; 51 return 0; 52 }