迷宫的最短路径(bfs)

宽度优先搜索（BFS，Breadth-First Search）也是搜索的手段之一，与深度优先搜索类似，从某个状态出发搜索所有可以到达的状态。

与深度优先搜索的不同之处在于搜索的顺序，宽度优先搜索总是先搜索距离初始状态最近的状态。也就是说，它是按照开始状态→只需一次转移就能到达的所有状态→只需2次就可以到达的所有状态→…按照这样的顺序进行搜索。对于同一个状态，宽度优先搜索只经过一次，因此时间复杂度为O（状态数×转移的方式）。

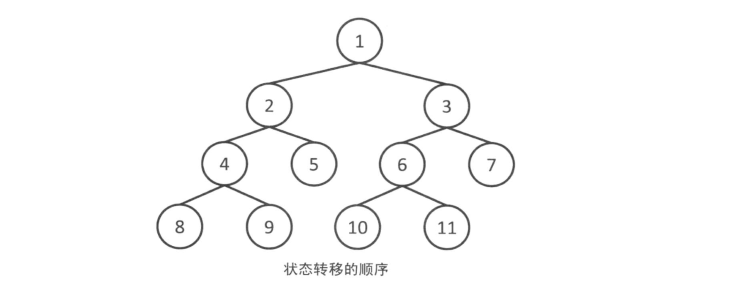
深度优先搜索利用了栈进行计算，而宽度优先搜索则利用了队列进行计算。搜索时首先将状态添加进队列里，此后从队列的最前端不断取出状态，把从该状态可以转移到的状态尚未访问过的部分加入到队列中，如此往复，直至队列被取空或找到了问题的解。通过观察这个队列，我们就可以知道所有的状态都是按照距初始状态由近及远的顺序遍历的。

例题：

迷宫的最短路径

　　给定一个大小为N×M的迷宫。迷宫由通道和墙壁组成，每一步可以向邻接的上下左右四个的通道移动。请求出从起点到终点所需的最小步数。请注意，本题假定从起点一定可以移动到终点。（N,M≤100）（'#', '.' , 'S', 'G'分别表示墙壁、通道、起点和终点）

输入：

10 10

#S######.#
......#..#
.#.##.##.#
.#........
##.##.####
....#....#
.#######.#
....#.....
.####.###.
....#...G#

输出：

22

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#define N 105
#define inf 1000000000
using namespace std;
int dir[4][2]={{1,0},{-1,0},{0,1},{0,-1}};
char k[N][N];
int vis[N][N];
int n,m;
int px,py,nx,ny;
typedef pair<int,int> p;
queue<p> q;
int bfs(){
  while(q.size()){
    p r=q.front();q.pop();
    if(r.first==nx&&r.second==ny){
      break;
    }
    for(int i=0;i<4;i++){
      int xx=r.first+dir[i][0];
      int yy=r.second+dir[i][1];
      if(xx>=0&&xx<=n&&yy>=0&&yy<=m&&k[xx][yy]!='#'&&vis[xx][yy]==inf){
        q.push(p(xx,yy));
        vis[xx][yy]=vis[r.first][r.second]+1;
    }
  }
}
return vis[nx][ny];
}
int main(){
  cin>>n>>m;
  for(int i=0;i<n;i++)
    for(int j=0;j<m;j++)
      vis[i][j]=inf;
  for(int i=0;i<n;i++)
    for(int j=0;j<m;j++){
      cin>>k[i][j];
      if(k[i][j]=='S')
        px=i,py=j;
      if(k[i][j]=='G')
        nx=i,ny=j;
    }
  q.push(p(px,py));
  vis[px][py]=0;
  printf("%d
",bfs());
  return 0;
}