算法入门刷题笔记 算法竞赛入门经典++第六章例题 6-6--6-9，6-12，6-14，6-15 树与二叉树

写在前面

好久没更新公众号和博客了，因为最近在研究新的方向，所以很少发文。
笔者接触编程只有一年，这一年间主要研究启发式算法在运筹学中的应用。但是由于编程基础薄弱，在进一步研究复杂运筹学问题时发现基础算法不过关导致写出的代码运行速度很慢，因此很苦恼。所以决定这个暑假补习一下基础算法，主要是刷一些简单的ACM入门题。偶尔会发一些刷题笔记（偶尔！）。和作者有类似目标的同学可以一起交流共勉！

目前在看的教程：
北京理工大学ACM冬季培训课程

算法竞赛入门经典/刘汝佳编著．－2版
点击下载

课程刷题点
Virtual Judge

刷题代码都会放在github上，欢迎一起学习进步！

6-6 Dropping Balls

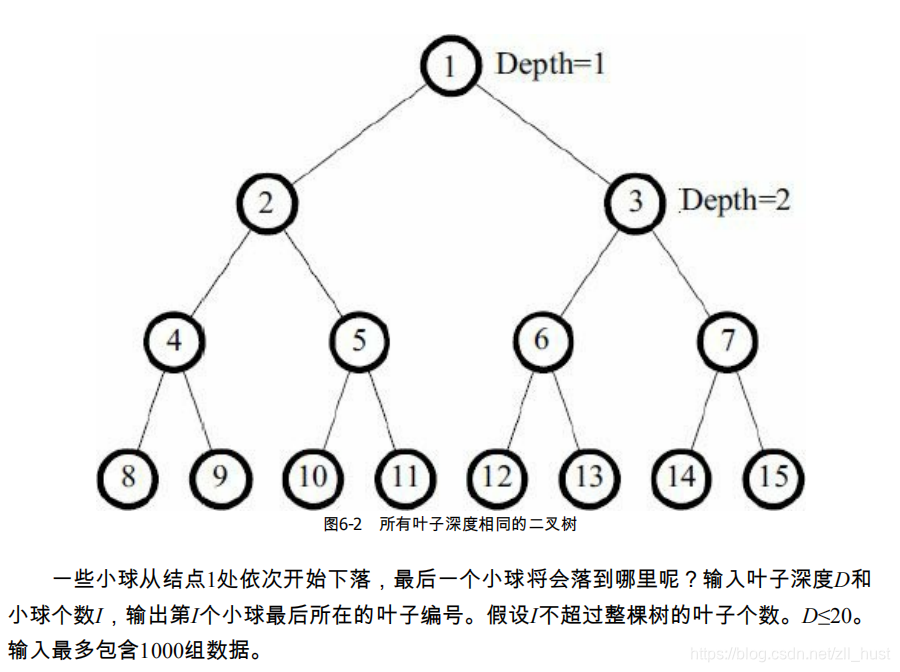
模拟小球掉落的情况。我一开始想，这个应该有公式，毕竟特征很明显，应该可以转化为包含$2^k+n$的公式。事实也确实如此。

书中一开始是从模拟角度出发，直接模拟每个节点的开关。但是计算量太大，可能造成TLE，所以改善为不断除二的方式优化模拟过程，余数为1则往左走，余数为0则往右走。其实和公式是类似的，相当于模拟了计算过程。

#include <iostream>
#include <sstream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <stack>
#include <unordered_map>
using namespace std;

typedef long long ll;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

void swap(int &x, int &y)
{
    int temp = x;
    x = y;
    y = temp;
}

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    int kase;
    cin >> kase;
    int D, I;
    while (scanf("%d%d", &D, &I) == 2)
    {
        int k = 1;
        for (int i = 0; i < D - 1; i++)
            if (I % 2)
            {
                k = k * 2;
                I = (I + 1) / 2;
            }
            else
            {
                k = k * 2 + 1;
                I /= 2;
            }
        printf("%d
", k);
    }

    return 0;
}

6-7 Trees on the level

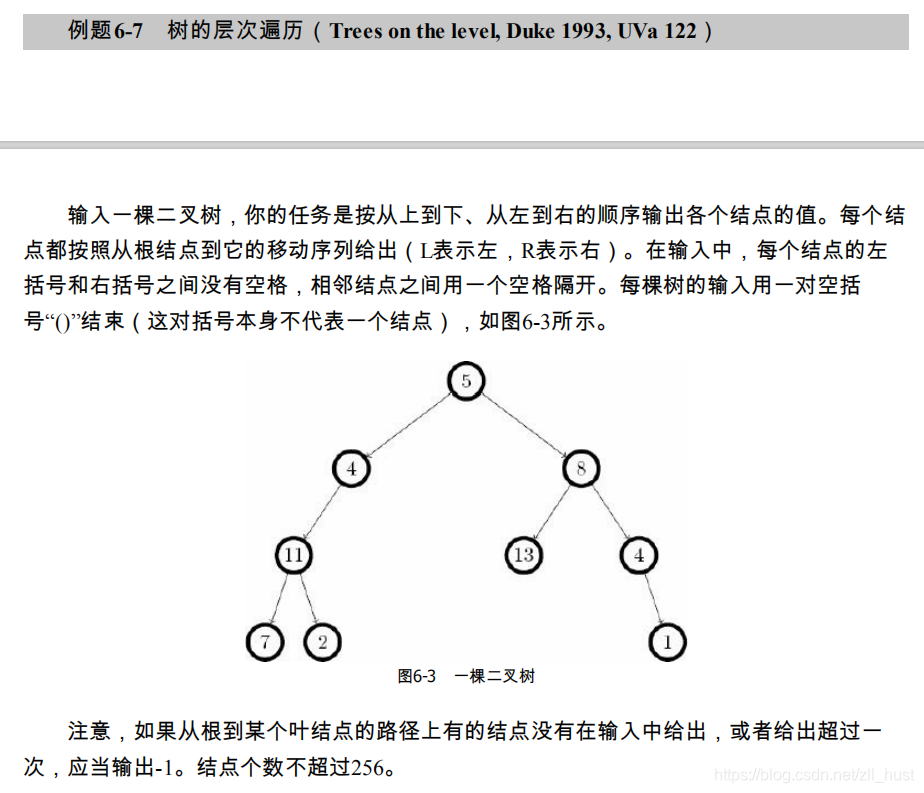
注意是不完全二叉树，256个节点意味着最大可能达到$2^{256}$的级别，开数组是不行的，所以考虑动态分配内存。书中直接用指针模拟二叉树，就当练习一下了。

C++没有自动内存清理机制，最好清理一下内存。

代码自建了比较完善的二叉树，很值得认真阅读。

#include <iostream>
#include <sstream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <stack>
#include <unordered_map>
using namespace std;

typedef long long ll;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

void swap(int &x, int &y)
{
    int temp = x;
    x = y;
    y = temp;
}

//结点类型
struct Node
{
    bool have_value; //是否被赋值过
    int v;           //结点值
    Node *left, *right;
    Node() : have_value(false), left(NULL), right(NULL) {} //构造函数
};
Node *root; //二叉树的根结点
bool failed;

Node *newnode() { return new Node(); }

void addnode(int v, string s)
{
    int n = s.length();
    Node *u = root; //从根结点开始往下走
    for (int i = 0; i < n; i++)
    {
        if (s[i] == 'L')
        {
            if (u->left == NULL)
                u->left = newnode(); //结点不存在，建立新结点
            u = u->left;             //往左走
        }
        else if (s[i] == 'R')
        {
            if (u->right == NULL)
                u->right = newnode();
            u = u->right;
        } //忽略其他情况，即最后那个多余的右括号
    }
    if (u->have_value)
        failed = true; //已经赋过值，表明输入有误
    u->v = v;
    u->have_value = true; //别忘记做标记
}

void remove_tree(Node *u)
{
    if (u == NULL)
        return;            //提前判断比较稳妥
    remove_tree(u->left);  //递归释放左子树的空间
    remove_tree(u->right); //递归释放右子树的空间
    delete u;              //调用u的析构函数并释放u结点本身的内存
}

bool read_input()
{
    failed = false;
    remove_tree(root); //释放内存
    root = newnode();  //创建根结点

    while (true)
    {
        string str;
        if (!(cin >> str))
            return false;
        if (str == "()")
            return true;
        str = str.substr(1, str.length() - 2);
        str[str.find(',')] = ' ';
        stringstream input(str);
        int id;
        string pos;
        input >> id >> pos;
        addnode(id, pos); //查找逗号，然后插入结点
    }
    return true;
}

bool bfs(vector<int> &ans)
{
    queue<Node *> q;
    ans.clear();
    q.push(root); //初始时只有一个根结点
    while (!q.empty())
    {
        Node *u = q.front();
        q.pop();
        if (!u->have_value)
            return false;    //有结点没有被赋值过，表明输入有误
        ans.push_back(u->v); //增加到输出序列尾部
        if (u->left != NULL)
            q.push(u->left); //把左子结点（如果有）放进队列
        if (u->right != NULL)
            q.push(u->right); //把右子结点（如果有）放进队列
    }
    return true; //输入正确
}

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    while (read_input())
    {
        vector<int> ans;
        if (bfs(ans))
        {
            for (int i = 0; i < ans.size(); i++)
                cout << ans[i] << " ";
            cout << endl;
        }
        else
            cout << "not complete" << endl;
    }
    return 0;
}

6-8 Tree

直白的标题…

通过中序遍历和后序遍历构造二叉树，再通过dfs搜索最短路。也可以在构造二叉树的过程中搜索最短路，太麻烦了我就不管了…

一开始搜中序后序构造二叉树，看到的一篇文章和原书代码中的方法不一样。这里简单mark一下书里的方法。（为了防止忘记，我特地提前跑来写博客的）

先简单mark一下前中后序遍历：三个节点ABC，A为根节点，B为左节点，C为右节点，前序顺序是ABC（根节点排最先，然后同级先左后右）；中序顺序是BAC(先左后根最后右）；后序顺序是BCA（先左后右最后根）。

下面利用这幅图来讲下刘大爷代码里的方法。

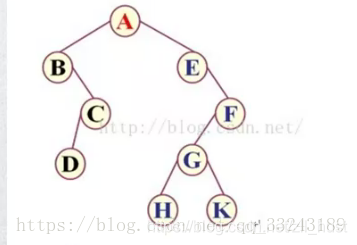
中序遍历：BDCAEHGKF

后序遍历：DCBHKGFEA

二叉树的方法都离不开递归。要构造二叉树，最重要的就是找到根节点然后递归。那么构造二叉树的要点就是找到根节点，然后划分左右子树范围，进一步递归。

后序遍历的特点是“左→右→根”，那么找到根节点就很容易。第一个根节点就是A。

中序遍历的特点是“左→根→右”，那么在知道根节点的情况下划分出左右节点的范围就很容易。比方说第一层划分时左子树就是A左边的BDC，右子树就是A右边的EHGKF。由此划分就可以知道左右子树的中序遍历字符串，以及左右子树节点的个数。

再回到后序遍历，知道了左右子树节点的个数，再根据“左→右→根”的特点划分出左右子树的范围就很容易了，直接取最前面n个（n代表左子树节点个数），就可以分开了。如第一层划分时，BDC是3个节点，那么在后序遍历中取前三个DCB，就是左子树的后序遍历。

核心代码在这里：

//把in_order[L1..R1]和post_order[L2..R2]建成一棵二叉树，返回树根
int build(int L1, int R1, int L2, int R2)
{
    if (L1 > R1)
        return 0; //空树
    int root = post_order[R2];
    int p = L1;
    while (in_order[p] != root)
        p++;
    int cnt = p - L1; //左子树的结点个数
    lch[root] = build(L1, p - 1, L2, L2 + cnt - 1);
    rch[root] = build(p + 1, R1, L2 + cnt, R2 - 1);
    return root;
}

完整代码：

#include <iostream>
#include <sstream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <stack>
#include <unordered_map>
using namespace std;

typedef long long ll;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

void swap(int &x, int &y)
{
    int temp = x;
    x = y;
    y = temp;
}

//因为各个结点的权值各不相同且都是正整数，直接用权值作为结点编号
const int maxv = 10000 + 10;
int in_order[maxv]; //中序
int post_order[maxv]; //后序
int lch[maxv]; //左子树编号
int rch[maxv]; //右子树编号
int n; //节点数量
bool read_list(int *a)
{
    string line;
    if (!getline(cin, line))
        return false;
    stringstream ss(line);
    n = 0;
    int x;
    while (ss >> x)
        a[n++] = x;
    return n > 0;
}

//把in_order[L1..R1]和post_order[L2..R2]建成一棵二叉树，返回树根
int build(int L1, int R1, int L2, int R2)
{
    if (L1 > R1)
        return 0; //空树
    int root = post_order[R2];
    int p = L1;
    while (in_order[p] != root)
        p++;
    int cnt = p - L1; //左子树的结点个数
    lch[root] = build(L1, p - 1, L2, L2 + cnt - 1);
    rch[root] = build(p + 1, R1, L2 + cnt, R2 - 1);
    return root;
}

int best, best_sum; //目前为止的最优解和对应的权和
void dfs(int u, int sum)
{
    sum += u;
    if (!lch[u] && !rch[u])//叶子，左子树和右子树为空
    { 
        if (sum < best_sum || (sum == best_sum && u < best))
        {
            best = u;
            best_sum = sum;
        }
    }
    if (lch[u])
        dfs(lch[u], sum);
    if (rch[u])
        dfs(rch[u], sum);
}
int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    while (read_list(in_order))
    {
        read_list(post_order);
        build(0, n - 1, 0, n - 1);
        best_sum = 1000000000;
        dfs(post_order[n - 1], 0);
        cout << best << "
";
    }
    return 0;
}

6-9 Trees on the level

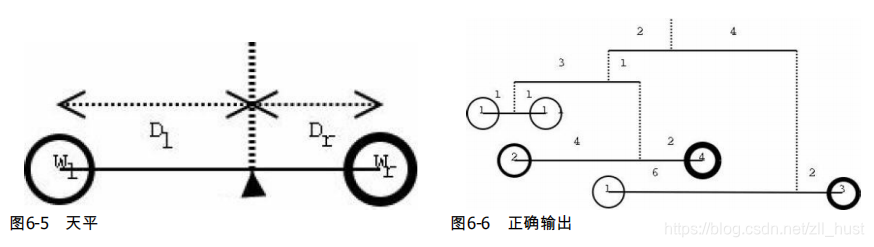
简单的二叉树，由于是输入是顺序遍历（根→左→右），所以可以一边输入一边判断叶子是否平衡，返回两片叶子质量总和。

#include <iostream>
#include <sstream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <stack>
#include <unordered_map>
using namespace std;

typedef long long ll;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

void swap(int &x, int &y)
{
    int temp = x;
    x = y;
    y = temp;
}

//输入一个子天平，返回子天平是否平衡，参数W修改为子天平的总重量
bool solve(int &W)
{
    int W1, D1, W2, D2;
    bool b1 = true, b2 = true;
    cin >> W1 >> D1 >> W2 >> D2;
    if (!W1)
        b1 = solve(W1);
    if (!W2)
        b2 = solve(W2);
    W = W1 + W2;
    return b1 && b2 && (W1 * D1 == W2 * D2);
}

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    int kase, W;
    cin >> kase;
    while (kase--)
    {
        if (solve(W))
            cout << "YES
";
        else
            cout << "NO
";
        if (kase)
            cout << "
";
    }
    return 0;
}

这题书里描述的有点诡异，其实就是在“#”和“@”构成的图里判断有多少块联通的@。其中斜对角线也算联通。

可以通过dfs遍历，或者bfs二重循环，反正图里只有两种符号，很好判断。

#include <iostream>
#include <sstream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <stack>
#include <unordered_map>
using namespace std;

typedef long long ll;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

void swap(int &x, int &y)
{
    int temp = x;
    x = y;
    y = temp;
}

const int maxn = 100 + 5;
char pic[maxn][maxn];
int m, n;
int idx[maxn][maxn]; //idx标记是否访问过

void dfs(int r, int c, int id)
{
    if (r < 0 || r >= m || c < 0 || c >= n)
        return; //"出界"的格子
    if (idx[r][c] > 0 || pic[r][c] != '@')
        return;     //不是"@"或者已经访问过的格子
    idx[r][c] = id; //连通分量编号 (其实标记为1就够了)
    for (int dr = -1; dr <= 1; dr++)
        for (int dc = -1; dc <= 1; dc++)
            if (dr != 0 || dc != 0)
                dfs(r + dr, c + dc, id);
}

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    while (scanf("%d%d", &m, &n) == 2 && m && n)
    {
        for (int i = 0; i < m; i++)
            scanf("%s", pic[i]);
        memset(idx, 0, sizeof(idx));
        int cnt = 0;
        for (int i = 0; i < m; i++)
            for (int j = 0; j < n; j++)
                if (idx[i][j] == 0 && pic[i][j] == '@')
                    dfs(i, j, ++cnt);
        printf("%d
", cnt);
    }
    return 0;
}

6-14 Abbotts Revenge

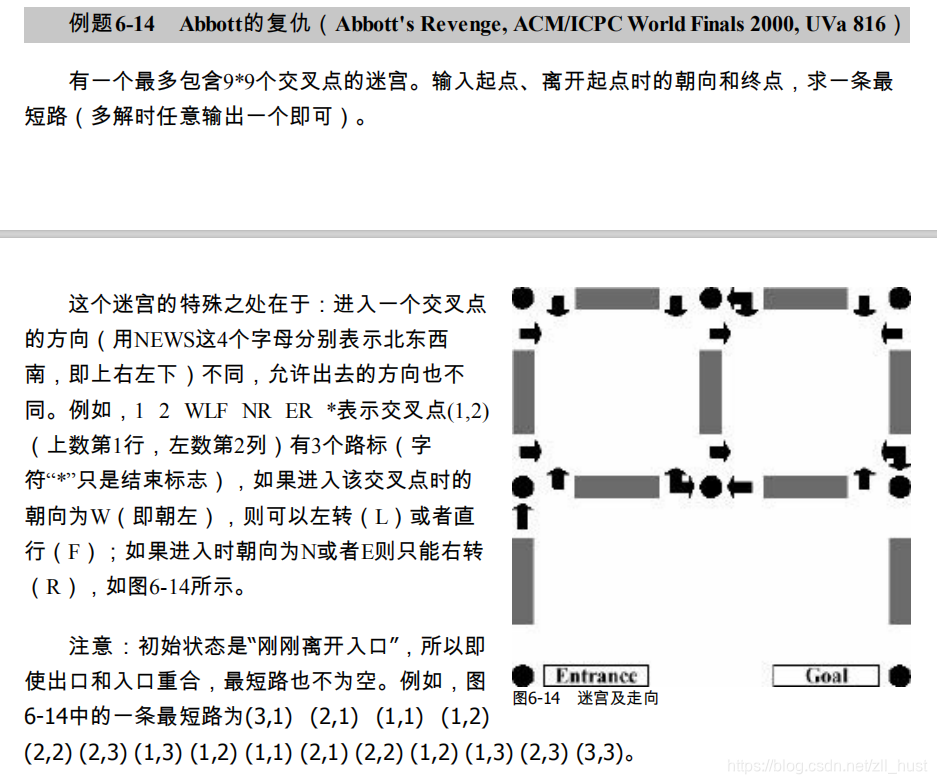
蛮复杂的题目，整了我好久…主要还是输入比较恶心…哎，早知道跳过了…（看评论区说输出也比较恶心，我都懒得submit了）（还要吐槽一句刘大爷能不能把代码放放全，放一半补了半年）

题目本身很简单，就是一个bfs走迷宫，只不过多加了一个方向，那就只需要加一个方向变量就好。

#include <iostream>
#include <sstream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <stack>
#include <unordered_map>
using namespace std;

typedef long long ll;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

struct Node
{
    int dir;
    int r; //row
    int c; //col
    Node()
    {
        r = 0;
        c = 0;
        dir = 0;
    }

    Node(int r, int c, int dir)
    {
        this->r = r;
        this->c = c;
        this->dir = dir;
    }
};

const char *dirs = "NESW"; //顺时针旋转
const char *turns = "FLR";
int dir_id(char c) { return strchr(dirs, c) - dirs; }
int turn_id(char c) { return strchr(turns, c) - turns; }
int has_edge[15][15][10][10]; //r,c,dir,trun是否可以行走
int d[15][15][10]; //最短路是否经过
Node pre[15][15][10]; //前一个点
int r_end, c_end, r1, c1, r_start, c_start, dir;
int inside[15][15];

const int dr[] = {-1, 0, 1, 0};
const int dc[] = {0, 1, 0, -1};
Node walk(const Node &u, int turn)
{
    int dir = u.dir;
    if (turn == 1)
        dir = (dir + 3) % 4; //逆时针
    if (turn == 2)
        dir = (dir + 1) % 4; //顺时针
    return Node(u.r + dr[dir], u.c + dc[dir], dir);
}

void print_ans(Node);
void solve() //bfs
{
    queue<Node> q;
    memset(d, -1, sizeof(d));
    Node u(r1, c1, dir);
    d[u.r][u.c][u.dir] = 0;
    q.push(u);
    while (!q.empty())
    {
        Node u = q.front();
        q.pop();
        if (u.r == r_end && u.c == c_end) //终点判断
        {
            print_ans(u);
            return;
        }
        for (int i = 0; i < 3; i++) //四个方向
        {
            Node v = walk(u, i);
            if (has_edge[u.r][u.c][u.dir][i] && inside[v.r][v.c] && d[v.r][v.c][v.dir] < 0) //存在边，存在点，未循环(循环则impossible)
            {
                d[v.r][v.c][v.dir] = d[u.r][u.c][u.dir] + 1;
                pre[v.r][v.c][v.dir] = u;
                q.push(v);
            }
        }
    }
    printf("No Solution Possible
");
}

void print_ans(Node u) //从目标结点逆序追溯到初始结点
{
    vector<Node> nodes;
    while(true)
    {
        nodes.push_back(u);
        if (d[u.r][u.c][u.dir] == 0)
            break;
        u = pre[u.r][u.c][u.dir];
    }
    nodes.push_back(Node(r_start, c_start, dir)); //打印解，每行10个
    int cnt = 0;
    for (int i = nodes.size() - 1; i >= 0; i--)
    {
        if (cnt % 10 == 0)
            printf(" ");
        printf(" (%d,%d)", nodes[i].r, nodes[i].c);
        if (++cnt % 10 == 0)
            printf("
");
    }
    if (nodes.size() % 10 != 0)
        printf("
");
}

int find(const char *str, char v)
{
    int len = strlen(str);
    for (int i = 0; i < len; i++)
        if (str[i] == v)
            return i;
    return -1;
}

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    char tag[20];
    while (scanf("%s", &tag) == 1)
    {
        if (tag[0] == 'E' && tag[1] == 'N' && tag[2] == 'D')
            break;
        printf("%s", tag);
        memset(d, -1, sizeof(d));
        memset(inside, -1, sizeof(inside));
        memset(has_edge, 0, sizeof(has_edge));
        char firstd;
        scanf("%d %d %c %d %d
", &r_start, &c_start, &firstd, &r_end, &c_end);
        inside[r_start][c_start] = 1;
        inside[r_end][c_end] = 1;
        dir = dir_id(firstd);
        r1 = r_start + dr[dir];
        c1 = c_start + dc[dir];
        while (true)
        {
            int r, c;
            scanf("%d", &r);
            if (r == 0)
                break;
            scanf("%d", &c);
            inside[r][c] = 1;
            char temp[20];
            memset(temp, 0, sizeof(temp));
            while (scanf("%s", &temp) == 1 && temp[0] != '*')
            {
                int *temp2 = has_edge[r][c][find(dirs, temp[0])];
                int len = strlen(temp);
                for (int i = 1; i < len; i++)
                    temp2[find(turns, temp[i])] = 1;
            }
        }
        solve();
    }

    return 0;
}

6-15 Ordering Tasks

不用看题目，只要知道是拓扑排序就好。

拓扑排序的特点是，入度为0的点可以放到队首；出度为0的点可以放到队尾。用dfs做就是找最深点，也就是出度为0的点，回溯时一层层放到队首。

#include <iostream>
#include <sstream>
#include <vector>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <string>
#include <set>
#include <queue>
#include <map>
#include <stack>
#include <unordered_map>
using namespace std;

typedef long long ll;
#define INT_MAX 0x7fffffff
#define INT_MIN 0x80000000
#define LOCAL

int t, n;
int c[105]; //访问状态
int topo[105];
int graph[105][105]; //记录有向边

bool dfs(int u)
{
    c[u] = -1; //正在访问
    for (int v = 0; v < n; v++)
        if (graph[u][v])
        {
            if (c[v] < 0)
                return false; //存在有向环，失败退出
            else if (!c[v] && !dfs(v))
                return false;
        }
    c[u] = 1;
    topo[--t] = u; //放到首部
    return true;
}

int main()
{
#ifdef LOCAL
    freopen("data.in", "r", stdin);
    // freopen("data.out", "w", stdout);
#endif
    int m;
    cin >> n >> m;
    for (int i = 0; i < m; i++)
    {
        int pre, nex;
        cin >> pre >> nex;
        graph[pre - 1][nex - 1] = 1;
    }

    t = n;
    memset(c, 0, sizeof(c));
    for (int i = 0; i < n; i++)
        if (!c[i])
            if (!dfs(i))
                cout << "impossible" << endl;

    for(int i = 0; i < n; i++)
        printf("%d ", topo[i] + 1);
    cout << endl;
    return 0;
}

Euler circuit

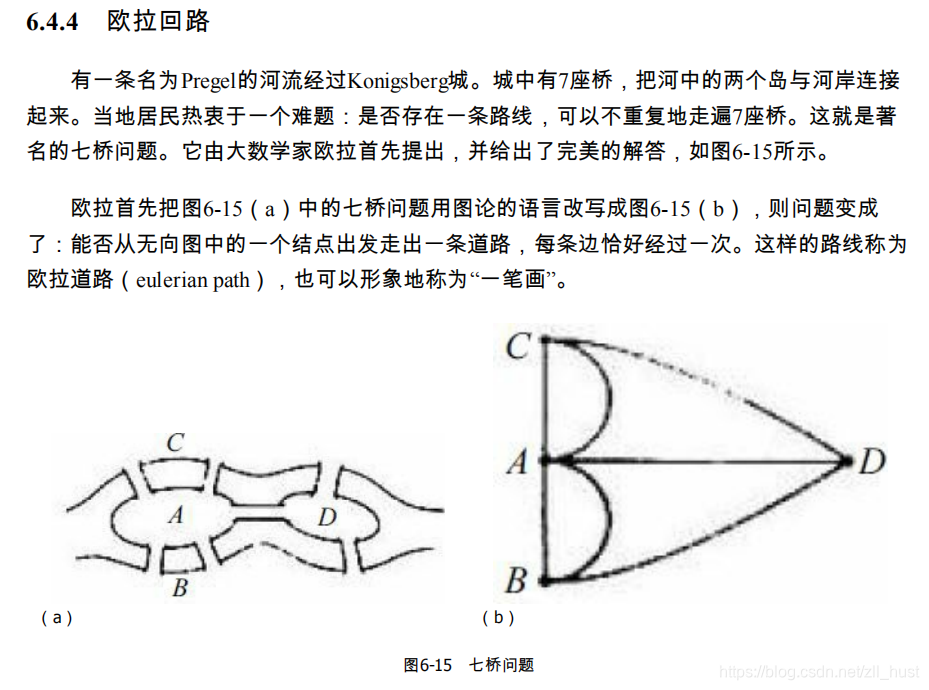
因为每条边都是要经过一次的，所以如果定点的度数为奇数，必然会出现停在这个点上无法移动的时候。有向图的结论进一步加强，相等一定是偶数。

（人家既然没证明充分条件，我也就不管了先吧~）