题目:Fansblog
题意大致描述:给定一个质数P(1e9≤P≤1e14),找到比P小的最大的质数Q,并求出Q!%P
需要了解的知识
在初等数论中,威尔逊定理给出了判定一个自然数是否为素数的充分必要条件。即:当且仅当p为素数时:( p -1 )! ≡ -1 ( mod p ),但是由于阶乘是呈爆炸增长的,其结论对于实际操作意义不大。
题解上给的是质数密度分布,我百度之后认为这个意思是两个质数之间相隔的不多,可以直接枚举找
逆元,逆元我们根据费马小定理可以很容易的求出来,经常用在分数和除法取模当中,逆元其实特别简单,用公式来说就是a的逆元等于a的(mod-2)次方,用一个快速幂就可以搞定。
公式的推理过程:
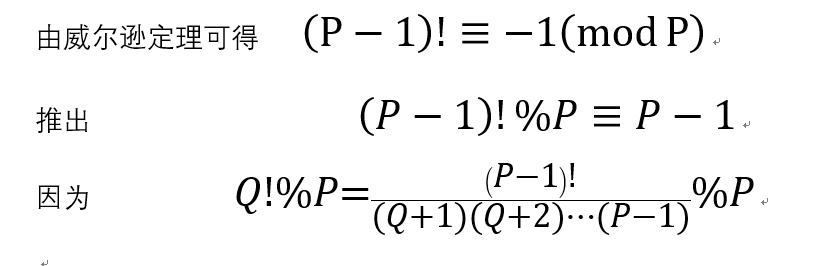
所以我们只需要从P-1开始找到Q为止,最后把P-1乘以(Q,P-1]的逆元就可以了
目前航电多校还不能补题,只过了样例,能补题了再回来改233
#include <iostream> #include <cstring> #include <string> #include <algorithm> #include <queue> #include <stack> #include <stdio.h> #include <cmath> #include <string.h> #define ll long long using namespace std; bool Is_prime(ll n) { if(n==1)return false; if(n==2)return true; for(register ll i=2;i*i<=n;i++) if(n%i==0)return false; return true; } long long Mode(long long a,long long b,ll m) { long long sum=1; a=a%m; while(b>0) { if(b%2==1) sum=(sum*a)%m; b/=2; a=(a*a)%m; } return sum; } int main() { //freopen("C:\Users\16599\Desktop\in.txt","r",stdin); int T; cin>>T; ll P; while(T--) { cin>>P; ll fz=P-1; ll fm=P-1; while(!Is_prime(fm)) { fz=fz*Mode(fm,P-2,P)%P; fm--; } cout<<fz<<endl; } return 0; }