转载自:http://blog.csdn.net/ggggiqnypgjg/article/details/6645824
manacher算法在O(n)的时间复杂度内解决了求字符串最大回文子串问题。
这个算法有一个很巧妙的地方,它把奇数的回文串和偶数的回文串统一起来考虑了。这个算法还有一个很好的地方就是充分利用了字符匹配的特殊性,避免了大量不必要的重复匹配。
算法大致过程是这样。
(1)先在每两个相邻字符中间插入一个分隔符,当然这个分隔符要在原串中没有出现过。一般可以用‘#’分隔。这样就非常巧妙的将奇数长度回文串与偶数长度回文串统一起来考虑了(见下面的一个例子,回文串长度全为奇数了),然后用一个辅助数组P记录以每个字符为中心的最长回文串的信息。P[id]记录的是以字符str[id]为中心的最长回文串,当以str[id]为第一个字符,这个最长回文串向右延伸了P[id]个字符。
原串: w aa bwsw f d
新串: # w# a # a # b# w # s # w # f # d #
辅助数组P: 1 2 1 2 3 2 1 2 1 2 1 4 1 2 1 2 1 2 1
这里有一个很好的性质,P[id]-1就是该回文子串在原串中的长度(包括‘#’)。如果这里不是特别清楚,可以自己拿出纸来画一画,自己体会体会。当然这里可能每个人写法不尽相同,不过我想大致思路应该是一样的吧。
好,我们继续。现在的关键问题就在于怎么在O(n)时间复杂度内求出P数组了。只要把这个P数组求出来,最长回文子串就可以直接扫一遍得出来了。
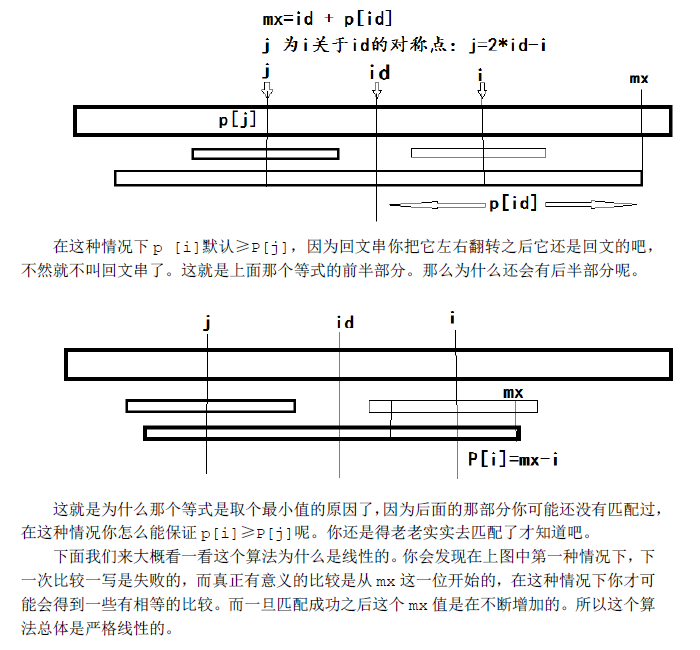
由于这个算法是线性从前往后扫的。那么当我们准备求P[i]的时候,i以前的P[j]我们是已经得到了的。我们用mx记在i之前的回文串中,延伸至最右端的位置。同时用id这个变量记下取得这个最优mx时的id值。
1 void pk() 2 { 3 int i; 4 int mx = 0; 5 int id; 6 for(i=1; i<n; i++) 7 { 8 if( mx > i ) 9 p[i] = MIN( p[2*id-i], mx-i ); 10 else 11 p[i] = 1; 12 for(; str[i+p[i]] == str[i-p[i]]; p[i]++) 13 ; 14 if( p[i] + i > mx ) 15 { 16 mx = p[i] + i; 17 id = i; 18 } 19 } 20 }