120. Triangle(动态规划 三角形最小路径 难 想)

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

For example, given the following triangle

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).

Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.

从下往上 

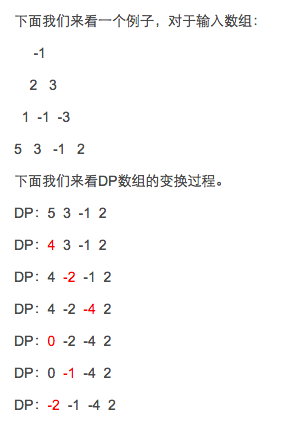
// Find the lesser of its two children, and sum the current value in the triangle with it

class Solution:
    def minimumTotal(self, a):
        """
        :type triangle: List[List[int]]
        :rtype: int
        """
        n = len(a)
        dp = a[n-1]
        for layer in range(0,n-1)[::-1]:
            for i in range(layer+1):
                dp[i] = min(dp[i],dp[i+1]) + a[layer][i]
        return dp[0]