89. 格雷编码

难度中等536收藏分享切换为英文接收动态反馈

n 位格雷码序列 是一个由 2n 个整数组成的序列，其中：

• 每个整数都在范围 [0, 2n - 1] 内（含 0 和 2n - 1）
• 第一个整数是 0
• 一个整数在序列中出现 不超过一次
• 每对 相邻 整数的二进制表示 恰好一位不同 ，且
• 第一个 和 最后一个 整数的二进制表示 恰好一位不同

给你一个整数 n ，返回任一有效的 n 位格雷码序列 。

示例 1：

输入：n = 2
输出：[0,1,3,2]
解释：
[0,1,3,2] 的二进制表示是 [00,01,11,10] 。
- 00 和 01 有一位不同
- 01 和 11 有一位不同
- 11 和 10 有一位不同
- 10 和 00 有一位不同
[0,2,3,1] 也是一个有效的格雷码序列，其二进制表示是 [00,10,11,01] 。
- 00 和 10 有一位不同
- 10 和 11 有一位不同
- 11 和 01 有一位不同
- 01 和 00 有一位不同

交替回溯

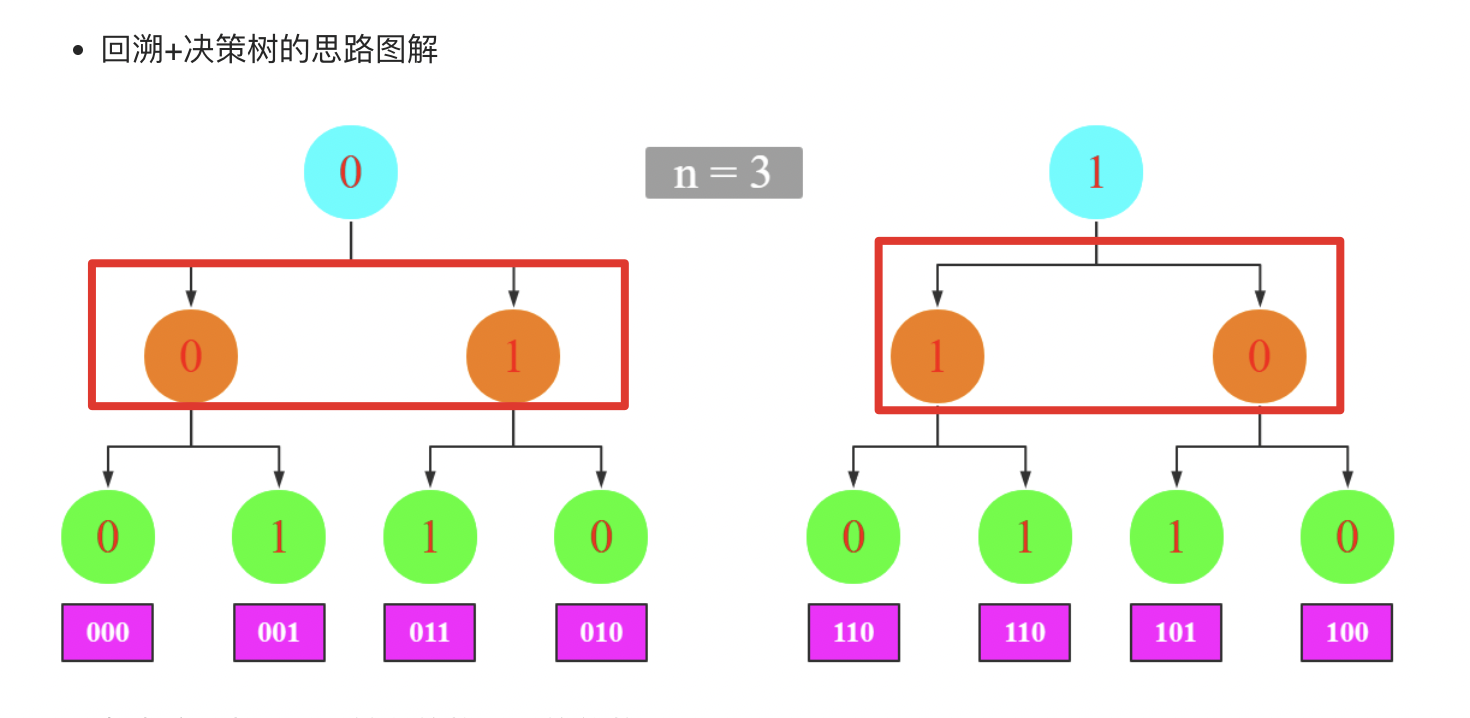
class Solution {
public:
    vector<int> res;
    void backtrack(string path, int k,int n,string choice) {
        if (n == k) {
            // 二进制转十进制
            int x = stoi(path, nullptr, 2);
            res.push_back(x);
            return;
        }
        backtrack(path+choice[0],k+1,n,"01");        
        backtrack(path+choice[1],k+1,n,"10");
        
    }
    vector<int> grayCode(int n) {
        string path = "";
        backtrack(path,0,n,"01");
        return res;
    }
};

class Solution {
public:
    vector<int> res;
    void backtrack(string& path, int k,int n,string choice) {
        if (n == k) {
            // 二进制转十进制
            int x = stoi(path, nullptr, 2);
            res.push_back(x);
            return;
        }
        path+=choice[0];
        backtrack(path,k+1,n,"01");        
        path.pop_back();
        
        path+=choice[1];
        backtrack(path,k+1,n,"10");
        path.pop_back();
    }
    vector<int> grayCode(int n) {
        string path = "";
        backtrack(path,0,n,"01");
        return res;
    }
};

class Solution {
public:
    vector<int> grayCode(int n) {
        vector<int> res;
        res.reserve(1<<n);// 2**n
        res.emplace_back(0);
        for(int i = 1; i <= n;i++) {
            int m = res.size();
            for(int j = m-1; j >=0 ;j--){
                res.emplace_back(res[j] | 1 << (i-1));
            }
        }
        return res;

    }
};

class Solution {
public:
    vector<int> res;
    void backtrack(bitset<32>& path, int k,int n) {
        if (n == k) {
            res.push_back(path.to_ulong());
            return;
        }
        backtrack(path,k+1,n);
        path.flip(n-k-1);// 从最高位开始反转
        backtrack(path,k+1,n);

    }
    vector<int> grayCode(int n) {
        bitset<32> path;
        backtrack(path,0,n);
        return res;
    }
};