给定一个字符串 s,返回 s 中不同的非空「回文子序列」个数 。
通过从 s 中删除 0 个或多个字符来获得子序列。
如果一个字符序列与它反转后的字符序列一致,那么它是「回文字符序列」。
如果有某个 i , 满足 ai != bi ,则两个序列 a1, a2, ... 和 b1, b2, ... 不同。
注意:
- 结果可能很大,你需要对
109 + 7取模 。
示例 1:
输入:s = 'bccb' 输出:6 解释:6 个不同的非空回文子字符序列分别为:'b', 'c', 'bb', 'cc', 'bcb', 'bccb'。 注意:'bcb' 虽然出现两次但仅计数一次。
示例 2:
输入:s = 'abcdabcdabcdabcdabcdabcdabcdabcddcbadcbadcbadcbadcbadcbadcbadcba' 输出:104860361 解释:共有 3104860382 个不同的非空回文子序列,104860361 对 109 + 7 取模后的值。
由于长字符串会依赖短字符串的回文序列数量,所以我们可以采用动态规划来实现。
设dp[i][j]表示字符串从i到j的回文序列个数,我们可以将长字符串看作短字符串左右加上两个字符
于是我们有s[i,j] = s[i] + s [i+1,j-1] + s[j],如:"bccb" 可以看作 "cc"两边分别加上"b",此时我们分情况进行讨论
(1)若s[i] == s[j],相当于我们给s[i+1,j-1] 左右加上两个相同的字符,然后我们计算回文序列的个数
①s[i+1,j-1]中没有字符和s[i]相等
设有字符串"bcb",则"bcb"的回文子序列是:b、c、bb、bcb
若两边加上相同的字符,相当于给"bcb"的回文子序列左右个加一个相同字符,仍然构成回文子序列
假设我们给"bcb"左右加一个字符"a",则相当于给"bcb"的子序列都左右加一个字符可构成新的回文子序列

在加上"a"(字符本身就是一个回文子序列)和"aa"(两个相同字符的回文子序列)
所以此时dp[i][j] = 2dp[i+1][j-1] + 2(本身的4个+新生成的4个+2个单独生成的)
②s[i+1,j-1]中有一个字符和s[i]相等
假设有一个字符相等,则之前已经记录了此单字符的回文子序列(只能加上"aa",不能加"a")
所以此时dp[i][j] = 2dp[i+1][j-1] + 1(本身的4个+新生成的4个+1个单独生成的)
③s[i+1,j-1]中有两个及以上字符和s[i]相等
若有两个及以上的字符,则我们需要找到其位置,并删掉重复计算的回文子序列,并且两个单独的之前也已经计算。
假设有字符串"dabcbad",我们向两边加入字符"a"
则此时的"a"字符会和中间的"bcb"组成重复的回文子序列,因为之前已经有"a"和"bcb"组成回文子序列
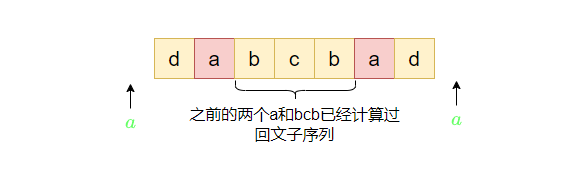

(2)若s[i] != s[j],则我们给之前任何一个回文子序列左右加上s[i]和s[j]都不能组成回文子序列,只能单独计算

综上所述,状态转移方程为:
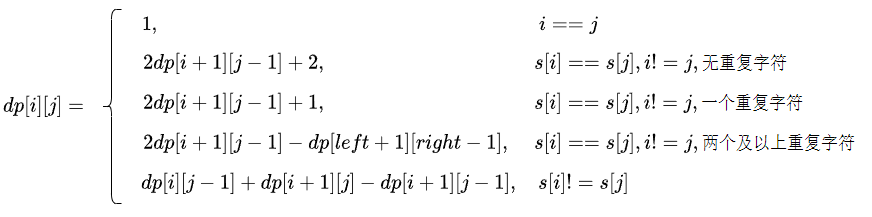
作者:capital-worker
链接:https://leetcode.cn/problems/count-different-palindromic-subsequences/solution/tong-ji-butong-by-jiang-hui-4-q5xf/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。