329. 矩阵中的最长递增路径(dp，bfs, 拓扑排序)

 

难度困难642收藏分享切换为英文接收动态反馈

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

 

 

 

BFS 

从每一个节点出发，像水波一样往外扩散，看它能扩散多远，然后记录所有节点的最大扩散路径长度即可。

 

class Solution {
public:

    int longestIncreasingPath(vector<vector<int>>& matrix) {

        int n = matrix.size();
        int m = matrix[0].size();
        
        queue<vector<int>> q;
        //假设每个数字都做为树的root
        for (int i = 0; i < n;i++) {
            for(int j = 0; j < m;j++) {
                q.push({i,j});
            }
        }
        
        int res = 0;
        vector<vector<int>> tt = {{-1,0},{1,0},{0,-1},{0,1}};
        while(!q.empty()) {
            int size = q.size();
            // 遍历当前层
            for (int k = 0; k < size; k++) {
                int i = q.front()[0];
                int j = q.front()[1];
                q.pop();
                // 遍历邻居
                for (auto t : tt) {
                    int new_i = i + t[0];
                    int new_j = j + t[1];
                    if (0 <= new_i && new_i < n && 0 <= new_j && new_j < m) {
                        if (matrix[i][j] < matrix[new_i][new_j]) {
                            q.push({new_i,new_j});     
                        }
                    }
                }
            }
            res++;
        }

        return res;
    }
};

 

 

拓扑排序

 

题目的意思已经非常明显了，某个节点上下左右的值只要比它大，就在它们之间连接一条有向边，比如下面这样：

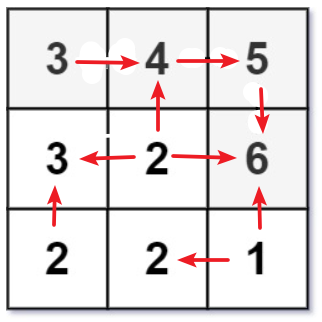
按照拓扑排序的思想，我们先把出度为 0 （即没有向外的箭头）的元素先入队，在上图中有 [3, 6, 2] 三个元素，然后遍历这三个元素，把指向它们的元素的出度减 1，如果减到0了，则把那个元素也入队，直到队列中没有元素为止。

class Solution {
public:

    int longestIncreasingPath(vector<vector<int>>& matrix) {

        int n = matrix.size();
        int m = matrix[0].size();
        
        queue<vector<int>> q;
        vector<vector<int>> tt = {{-1,0},{1,0},{0,-1},{0,1}};

        //先构图
        vector<vector<int>>outdegree(n,vector<int>(m,0));

        for (int i = 0; i < n;i++) {
            for(int j = 0; j < m;j++) {
                for (auto t :tt) {
                    int new_i = i + t[0];
                    int new_j = j + t[1];
                    if (0 <= new_i && new_i < n && 0 <= new_j && new_j < m && matrix[i][j] < matrix[new_i][new_j]) {
                        outdegree[i][j]++; 
                    }
                }
            }
        }

        for (int i = 0; i < n;i++) {
            for(int j = 0; j < m;j++) {
                if (outdegree[i][j] == 0) {
                    q.push({i,j});
                }
            }
        }
        int res = 0;
        while(!q.empty()) {
            int size = q.size();
            // 遍历当前层
            for (int k = 0; k < size; k++) {
                int i = q.front()[0];
                int j = q.front()[1];
                q.pop();
                // 遍历邻居
                for (auto t : tt) {
                    int new_i = i + t[0];
                    int new_j = j + t[1];
                    if (0 <= new_i && new_i < n && 0 <= new_j && new_j < m && matrix[i][j] > matrix[new_i][new_j]) {
                        outdegree[new_i][new_j]--;
                        if (outdegree[new_i][new_j]== 0) {
                            q.push({new_i,new_j});     
                        }
                    }
                }
            }
            res++;
        }

        return res;
    }
};

 

 

 

动态规划 

状态定义：dp[i][j]表示从 matrix[i, j] 位置出发的最长路径。

状态转移：dp[i][j]=max(dp[i'][j'] if matrix[i'][j'] > matrix[i][j]) + 1，表示dp[i][j]的值从相邻的比当前节点值大的节点中最长路径更长的转移而来。
初始状态：显然每个节点初始状态为1，表示初始时每个节点的最长路径就是当前节点本身。
这里的关键是，计算当前节点的时候要先把相邻的比它大的节点先计算出来。

比如，还是下面这张图，计算 3 的时候必须 4 的值已经计算出来了。

 

 

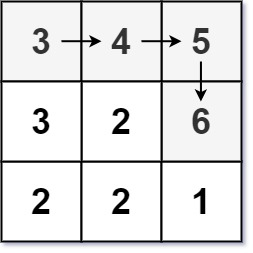
class Solution {
public:

    int longestIncreasingPath(vector<vector<int>>& matrix) {
        vector<vector<int>> num2ids;
        int n = matrix.size();
        int m = matrix[0].size();
        for (int i = 0; i < n;i++) {
            for(int j = 0; j < m;j++) {
                vector<int> temp = {matrix[i][j],i,j};
                num2ids.emplace_back(temp);
            }
        }
        // 记录从大到小排序的 index
        sort(num2ids.begin(),num2ids.end(),[](vector<int>a, vector<int>b)
        {
            return a[0]>b[0];
        });

        int res = 1;
        vector<vector<int>>dp(n,vector<int>(m,1));
        // 遍历的时候从大到小遍历
        for(auto num2id : num2ids) {
            int num = num2id[0];
            int i = num2id[1];
            int j = num2id[2];

            //max(dp[i-1][j] ,dp[i][j-1],dp[i+1][j],dp[i][j+1] if matrix[i][j] < matrix[i-1][j]
            vector<vector<int>> tt = {{-1,0},{1,0},{0,-1},{0,1}};
            int cur_max = 0;
            for (auto t : tt) {
                int new_i = i + t[0];
                int new_j = j + t[1];
                if (0 <= new_i && new_i < n && 0 <= new_j && new_j < m) {
                    if (matrix[i][j] < matrix[new_i][new_j]) {
                        cur_max = max(cur_max,dp[new_i][new_j]);
                    }
                }
                dp[i][j] = 1 + cur_max; 
                //cout <<i << " " << j << " " <<  dp[i][j] << endl;
                res = max(res,dp[i][j]);
            }
        }

        return res;
    }
};