# 定义
元学习,meta-learning,又叫learning to learn。传统的深度学习从头开始学习(训练),即learning from scratch,对算力和时间都是更大的消耗和考验。
元学习包括:
1、Zero-Shot/One-Shot/Few-Shot 学习.
2、模型无关元学习(Model Agnostic Meta Learning).
3、元强化学习(Meta Reinforcement Learning)
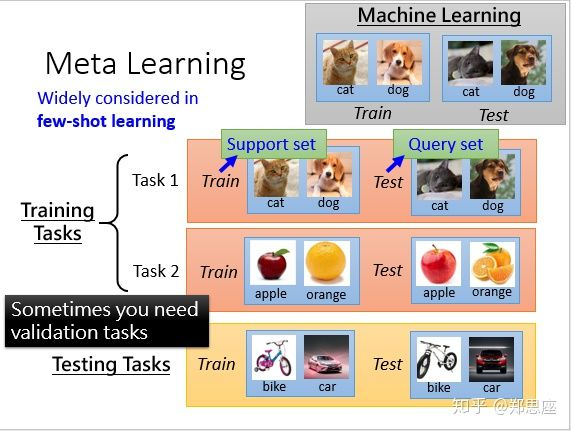
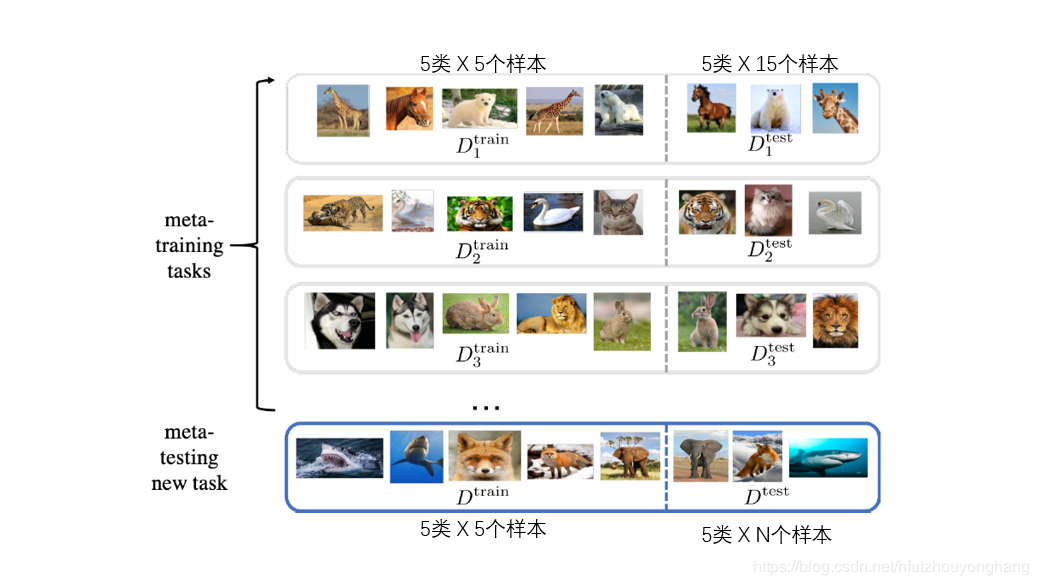
元学习的核心:task。元学习的训练样本和测试样本都是基于任务的。元学习的训练过程是在task1和task2上训练模型(更新模型参数),测试过程是在测试任务上评估模型好坏,从图中可以看出,测试任务和训练任务内容完全不同。
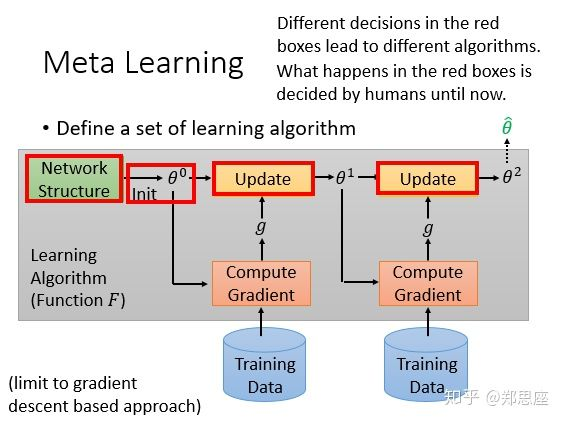
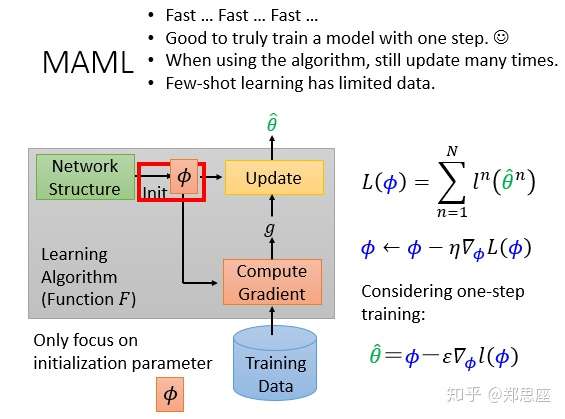
传统深度学习的操作方式如下图,先定义一个网络架构,初始化参数,然后通过自己选择的优化器更新参数,图中通过两次epoch更新最终得到网络输出 ,那元学习与传统深度学习的联系在哪儿呢?
注意到红色方框中的东西都是人为设计定义的,其实元学习的目标就是去自动学习或者说代替方框中的东西,不同的代替方式就发明出不同的元学习算法。比如说对于一个新任务的初始参数部分来说,如果能够提前获得一个来自其他任务学习到的较好的初始参数,可能经过很快的训练就能收敛到全局最优,也就是fast adaption。
以下两个经典算法都把学习目标定义在初始化参数的部分,所以接下来的解读都以此假设为学习目标。在神经网络算法,都需定义一个损失函数来评价模型好坏,元学习的损失通过N个任务的测试损失相加得到。定义在第n个任务上的测试损失是 ,则对于N个任务来说,总的损失为
,这就是元学习的优化目标。
MAML
Model Agnostic Meta Learning,简称MAML,发音酷似英文中的哺乳动物mammal,是近两年元学习领域的典型代表。理解MAML算法的损失函数含义和推导过程,首先得严格区分pre-training。我们定义初始化参数为 ,其初始化参数为
,定义在第n个测试任务上训练之后的模型参数为
,于是总的损失函数为
。pre-training的损失函数是
,直观上理解是MAML所评测的损失是在任务训练之后的测试loss,而pre-training是直接在原有基础上求损失没有经过训练。
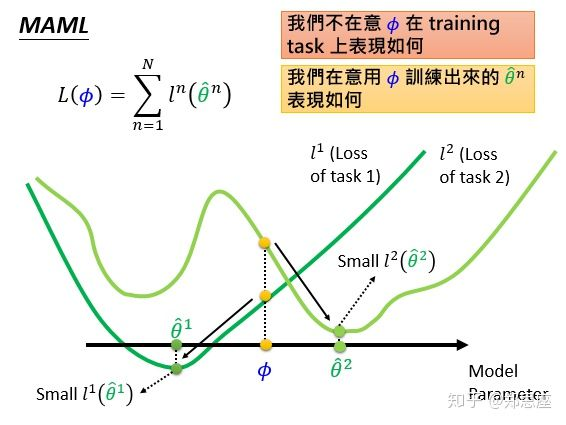
假设模型参数的 和
向量都是一维的,MAML不在乎当前参数在训练数据上loss的表现,MAML是找到一个不偏不倚的
,使得不管是在任务1的loss曲线
还是任务2的loss曲线
上,都能快速梯度下降到分别的全局最优。
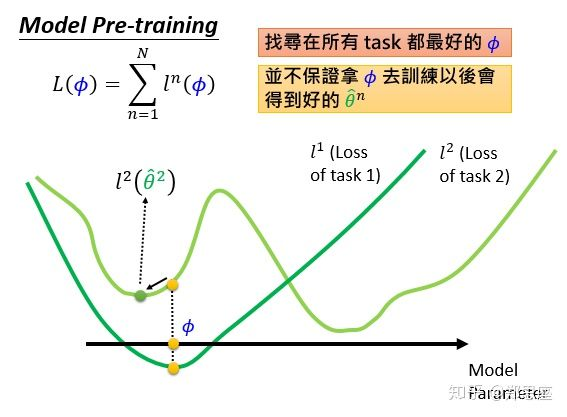
而model pre-training的初衷是寻找一个从一开始就让所有任务的损失之和处于最小状态 ,它并不保证所有任务都能训练到最好的
,如上图所示,
即收敛到局部最优。MAML比作选择读博,意味着在意的是以后的表现如何,即潜力;而model pre-training就相当于选择毕业直接去互联网大厂工作,马上就把所学技能兑现金钱,在意的是当下表现如何。
总结起来,MAML算法的框架其实很简单,值得注意的是两个学习率 和
所用的地方不同:
1、对于采样出来的所有任务 ,在support set上计算梯度并更新参数
2、计算所有任务在query set上的损失之和
3、更新初始化参数
这是训练过程的流程,所有的更新参数步骤都被限制在了一次,即one-step,但在用这个算法时,即测试新任务的表现时可以更新更多次。
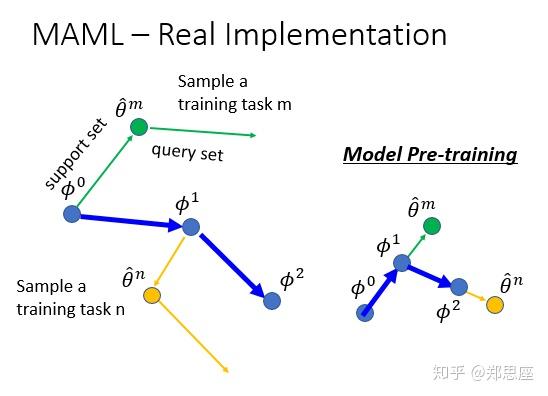
原始论文中提到一个词gradient by gradient,在左图体现得淋漓尽致,从 到
是流程中的第一步,在support set上训练得到;
继续往前一步是流程中的第二步,并不代表它又更新了,而是为了在query set上计算loss并把batch中的所有采样任务loss加起来(在图中batch为1);从
到
显而易见是第三步,沿着
梯度更新,这是第二次计算梯度。而从
到
是啥含义呢?是跑第二遍以上流程(包含三个步骤),更专业的术语叫做第二个epoch。接下来理解model pre-training简直就是易如反掌了,从
到
直接沿着步骤1的方向,没有gradien by gradient这一招。
用每个task 计算loss,更新参数seita,
把所有task 的loss(用每个task更新后的参数算) 加起来。更新梯度。

Reptile
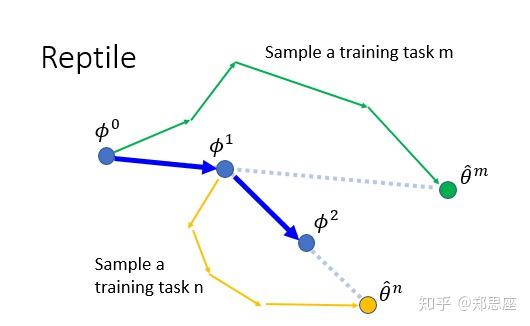
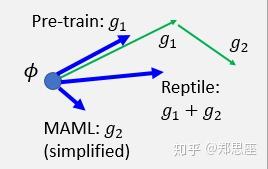
为什么叫reptile呢?因为从原论文上找不出任何蛛丝马迹,李宏毅老师开玩笑道可能是为了硬凑一个爬行动物。同样,我又要说一个词了,易如反掌——只要理解了上面的一切,理解Reptile的思想就是分分钟钟的事情。看图:简而言之,Reptile就是在算法流程中的第一步更新了多次,在第三步时用 到
的差向量作为更新方向。把MAML、model pre-training、Reptile三者的图放一起,用向量的运算规则,Reptile可以理解为前两者的梯度更新方向的综合。
https://www.youtube.com/watch?v=vUwOA3SNb_E&list=PLJV_el3uVTsOK_ZK5L0Iv_EQoL1JefRL4&index=36