七大查找十大排序算法（一）

转载自：https://www.cnblogs.com/wxisme/p/5243631.html

七大查找——十大排序算法

查找算法：顺序查找、插值查找（二分查找、斐波那契查找、插值查找）、哈希表查找、二叉树排序查找（树表查找）、分块查找

排序算法：内部排序{交换类排序（堆排序、快速排序）、选择类排序（简单选择排序、堆排序）、插入排序（直接插入排序、希尔排序）归并排序}

　　　　　外部排序{计数排序、基数排序、桶排序}

　　　　　图片来源：https://blog.csdn.net/u011552404/article/details/78973058

　　　　　查找：

　　　　　

 

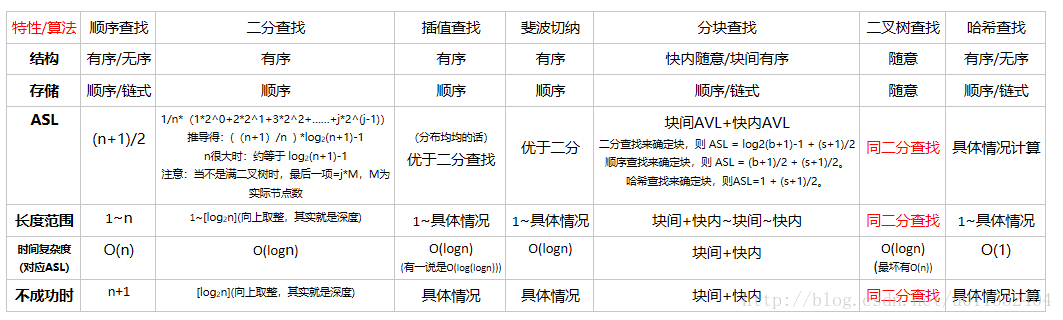
　　　　　排序：

　　　　　

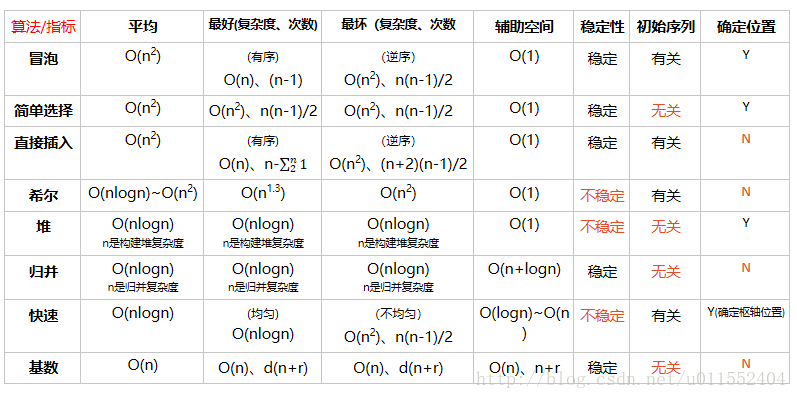
一、查找

　　数据结构——七大查找算法

　　查找是在大量的信息中寻找一个特定的信息元素，在计算机应用中，查找是常用的基本运算，例如编译程序中符号表的查找。本文简单概括性的介绍了常见的七种查找算法，说是七种，其实二分查找、插值查找以及斐波那契查找都可以归为一类——插值查找。插值查找和斐波那契查找是在二分查找的基础上的优化查找算法

　　

查找定义：根据给定的某个值，在查找表中确定一个其关键字等于给定值的数据元素（或记录）。

　　查找算法分类： 
　　1）静态查找和动态查找； 
　　　　注：静态或者动态都是针对查找表而言的。动态表指查找表中有删除和插入操作的表。 
　　2）无序查找和有序查找。 
　　　　无序查找：被查找数列有序无序均可； 
　　　　有序查找：被查找数列必须为有序数列。 
　　平均查找长度（Average Search Length，ASL）：需和指定key进行比较的关键字的个数的期望值，称为查找算法在查找成功时的平均查找长度。 
　　对于含有n个数据元素的查找表，查找成功的平均查找长度为：ASL = Pi*Ci的和。 
　　Pi：查找表中第i个数据元素的概率。 
　　Ci：找到第i个数据元素时已经比较过的次数。

在大量数据中常用的查找数据的做法有四类：顺序查找，二分查找，二叉树查找（BST），红黑树查找（RBT）。 
这四类查找方法分别对应着四种基本思想原理：

顺序查找 —— 无序简单查找

二分查找 —— 有序查找，每次折半搜索，插入数据费时

二叉树查找（BST） —— 不平衡二叉树有序查找，插入与搜索综合性能较优

红黑树查找（RBT） —— 平衡二叉树有序查找，插入与搜索综合性能最优

注：从上至下平均性能变优，算法难度增大，后三种查找为有序查找

　　1、顺序查找

　　说明：顺序查找适合于存储结构为顺序存储或链接存储的线性表。 
　　基本思想：顺序查找也称为线形查找，属于无序查找算法。从数据结构线形表的一端开始，顺序扫描，依次将扫描到的结点关键字与给定值k相比较，若相等则表示查找成功；若扫描结束仍没有找到关键字等于k的结点，表示查找失败。 
　　复杂度分析：　 
　　查找成功时的平均查找长度为：（假设每个数据元素的概率相等） ASL = 1/n(1+2+3+…+n) = (n+1)/2 ; 
　　当查找不成功时，需要n+1次比较，时间复杂度为O(n); 
　　所以，顺序查找的时间复杂度为O(n)。

　　C++实现源码：

　　//顺序查找
　　int SequenceSearch(int a[], int value, int n)
　　{
　　int i;
　　for(i=0; i<n; i++)
　　if(a[i]==value)
　　return i;
　　return -1;
　　}

java实现源码：

public class sequence{

public static  boolean SequenceSearch(int a[],int k,int value){

for( int i = 0 ; i<k;i++){

if( value == a[i])

return true;

else

return false;

}

return false;

}

public static void main(String[] args) {

int[] a = {8,2,4,5,3,10,11,6,9};

System.out.println(SequenceSearch(a,a.length,20));

}

}

//printf: false

2、折半查找 （二分查找）

说明：元素必须是有序的，如果是无序的则要先进行排序操作。

　　基本思想：也称为二分查找，属于有序查找算法。用给定值k先与中间结点的关键字比较，中间结点把线形表分成两个子表，若相等则查找成功；若不相等，再根据k与该中间结点关键字的比较结果确定下一步查找哪个子表，这样递归进行，直到查找到或查找结束发现表中没有这样的结点。

　　复杂度分析：最坏情况下，关键词比较次数为log2(n+1)log2(n+1)，且期望时间复杂度为O(log2n)O(log2n)；

　　注：折半查找的前提条件是需要有序表顺序存储，对于静态查找表，一次排序后不再变化，折半查找能得到不错的效率。但对于需要频繁执行插入或删除操作的数据集来说，维护有序的排序会带来不小的工作量，那就不建议使用。——《大话数据结构》 
　　 
　　折半查找算法要求数组本身是排序好的，折半查找算法每次可以排除掉一半的数字，采用了递归的方法。折半查找法不适合采用链式物理结构。 
实现代码：

/*查找算法练习*/
#include<stdio.h>
int search(int*p_num,intsize,int num){
    int pos = 0;
    for (pos = 0;pos <= size - 1;pos++){
        if (*(p_num + pos) == num){
            return pos;
        }
    }
}

 //折半查找函数

int half_search(int*p_num,intsize,int num){
    if (size > 0){
        if (*(p_num + size / 2) == num){
            returnsize / 2;
        }
        elseif (*(p_num + size / 2) > num){
            return half_search(p_num,size / 2,num);
        }
        else {
            return half_search(p_num + size / 2 + 1,size -
                    size / 2 - 1,num) + size / 2 + 1;   
        }
    }
    else {
        return -1;
        }
}

int main(){
    //int num[] = {6,9,3,2,10,7,8};int num[] = {1,2,3,4,5,6,7,8};
    printf("数字7的下标是%d
",half_search(num,8,7));
    return0;
}

java实现源码：

/*1.*/

public class BinarySearch1{

 

public static int binarysearch(int[] a,int n,int value){

int low = 0;

int high = n - 1;

int mid;

while(low < high){

mid = (low + high)/2;

if(value < a[mid])

high = mid - 1;

if(value > a[mid])

low = mid + 1;

if(value == a[mid])

return mid;

}

return -1;

}

public static void main(String[] args) {

//int[] a = {1,4,2,9,8,6,7,0,3,5}

int[] a = {0,1,2,3,4,5,6,7,8,9};

System.out.println(binarysearch(a,a.length,7));

} 

}

3、插值查找

在介绍插值查找之前，首先考虑一个新问题，为什么上述算法一定要是折半，而不是折四分之一或者折更多呢？ 
　　打个比方，在英文字典里面查“apple”，你下意识翻开字典是翻前面的书页还是后面的书页呢？如果再让你查“zoo”，你又怎么查？很显然，这里你绝对不会是从中间开始查起，而是有一定目的的往前或往后翻。 
　　同样的，比如要在取值范围1 ~ 10000 之间 100 个元素从小到大均匀分布的数组中查找5， 我们自然会考虑从数组下标较小的开始查找。 
　　经过以上分析，折半查找这种查找方式，不是自适应的（也就是说是傻瓜式的）。二分查找中查找点计算如下： 
　　mid=(low+high)/2, 即mid=low+1/2*(high-low); 
　　通过类比，我们可以将查找的点改进为如下： 
　　mid=low+(key-a[low])/(a[high]-a[low])*(high-low)， 
　　也就是将上述的比例参数1/2改进为自适应的，根据关键字在整个有序表中所处的位置，让mid值的变化更靠近关键字key，这样也就间接地减少了比较次数。 
　　基本思想：基于二分查找算法，将查找点的选择改进为自适应选择，可以提高查找效率。当然，插值查找也属于有序查找。 
　　注：对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。 
　　复杂度分析：查找成功或者失败的时间复杂度均为O(log2(log2n))。 
　　C++实现源码： 

/插值查找

//二分查找（折半查找），版本1
int BinarySearch1(int a[], int value, int n)
{
    int low, high, mid;
    low = 0;
    high = n-1;
    while(low<=high)
    {
        mid = (low+high)/2;
        if(a[mid]==value)
            return mid;
        if(a[mid]>value)
            high = mid-1;
        if(a[mid]<value)
            low = mid+1;
    }
    return -1;
}
 
//二分查找，递归版本
int BinarySearch2(int a[], int value, int low, int high)
{
    int mid = low+(high-low)/2;
    if(a[mid]==value)
        return mid;
    if(a[mid]>value)
        return BinarySearch2(a, value, low, mid-1);
    if(a[mid]<value)
        return BinarySearch2(a, value, mid+1, high);
}

java实现源码：

/*1.*/
public class BinarySearch1{
    
    public static int binarysearch(int[] a,int n,int value){
        int low = 0;
        int high = n - 1;
        int mid;
        while(low < high){
            mid = (low + high)/2;
            if(value < a[mid])
                high = mid - 1;
            if(value > a[mid])
                low = mid + 1;
            if(value == a[mid])
                return mid;
        }
        return -1;
    }
    public static void main(String[] args) {
        //int[] a = {1,4,2,9,8,6,7,0,3,5}
        int[] a = {0,1,2,3,4,5,6,7,8,9};
        System.out.println(binarysearch(a,a.length,7));
    } 
}

4、斐波那契查找

在介绍斐波那契查找算法之前，我们先介绍一下很它紧密相连并且大家都熟知的一个概念——黄金分割。

　　黄金比例又称黄金分割，是指事物各部分间一定的数学比例关系，即将整体一分为二，较大部分与较小部分之比等于整体与较大部分之比，其比值约为1:0.618或1.618:1。

　　0.618被公认为最具有审美意义的比例数字，这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐、建筑等艺术领域，而且在管理、工程设计等方面也有着不可忽视的作用。因此被称为黄金分割。

　　大家记不记得斐波那契数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…….（从第三个数开始，后边每一个数都是前两个数的和）。然后我们会发现，随着斐波那契数列的递增，前后两个数的比值会越来越接近0.618，利用这个特性，我们就可以将黄金比例运用到查找技术中。

　　基本思想：也是二分查找的一种提升算法，通过运用黄金比例的概念在数列中选择查找点进行查找，提高查找效率。同样地，斐波那契查找也属于一种有序查找算法。

　　相对于折半查找，一般将待比较的key值与第mid=（low+high）/2位置的元素比较，比较结果分三种情况：

　　 1）相等，mid位置的元素即为所求

　　 2）>，low=mid+1;

        3）<，high=mid-1。

　　斐波那契查找与折半查找很相似，他是根据斐波那契序列的特点对有序表进行分割的。他要求开始表中记录的个数为某个斐波那契数小1，及n=F(k)-1;

 开始将k值与第F(k-1)位置的记录进行比较(及mid=low+F(k-1)-1),比较结果也分为三种

　　1）相等，mid位置的元素即为所求

　　2）>，low=mid+1,k-=2;

　　    说明：low=mid+1说明待查找的元素在[mid+1,high]范围内，k-=2 说明范围[mid+1,high]内的元素个数为n-(F(k-1))= Fk-1-F(k-1)=Fk-F(k-1)-1=F(k-2)-1个，所以可以递归的应用斐波那契查找。

　　3）<，high=mid-1,k-=1。

　　    说明：low=mid+1说明待查找的元素在[low,mid-1]范围内，k-=1 说明范围[low,mid-1]内的元素个数为F(k-1)-1个，所以可以递归 的应用斐波那契查找。

　　复杂度分析：最坏情况下，时间复杂度为O(log2n)，且其期望复杂度也为O(log2n)。

 

public class Fibonacci {

    public static void main(String[] args) {
        int[] arr = {1, 8, 10, 89, 1000, 1234};
        System.out.println(fibSearch(arr , 99));
    }

    public static int maxSize = 20;

    public static int[] fib() {
        int[] f = new int[maxSize];
        f[0] = 1;
        f[1] = 1;
        for(int i = 2; i < maxSize; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }
        return f;
    }

    // 斐波那契查找（其实就是每次查找的点，都接近把数组划分成0.618比率，左边元素个数/总元素个数 约等于 0.618）
    // 大致就是想要每次查找按照（查找点左侧元素/总元素个数）接近0.618的比率获取查找元素下标。
    // 因为斐波那契查找，相邻两项前后的比值接近0.618，然后就根据斐波那契数列的规律利用到查找算法中。
    public static int fibSearch(int[] a, int key) {
        int low = 0;
        int high = a.length - 1;
        // 表示斐波那契分割数值的下标
        int k = 0;
        int mid = 0;
        int f[] = fib();
        // 获取斐波那契分割数值下标，根据查找数组的长度，决定需要多少个斐波那契数值
        while(high > f[k] - 1) {
            k++;
        }
        // 因为f[k]值可能大于a的长度，因此我们需要使用Arrays类，构造一个新的数组，并指向a[]
        // 不足的部分会使用0填充
        int[] temp = Arrays.copyOf(a, f[k]);
        // 实际上需求使用a数组最后的数填充temp
        // 例如：temp = {1,8,10,89,1000,1234,0,0,0} => {1,8,10,89,1000,1234,1234,1234}
        for(int i = high + 1; i < temp.length; i++) {
            temp[i] = a[high];
        }
        // 使用while来循环处理，找到我们的数key
        while(low <= high) {
            mid = low + f[k - 1] - 1;
            // 我们应该继续向数组左边查找
            if(key < temp[mid]) {
                high = mid - 1;
                // 为什么是k--
                // 全部元素 = 前面元素 + 后边元素 f[k] = f[k - 1] + f[k - 2]
                // 因为前面有f[k - 1]个元素，所以可以继续拆分f[k - 1] = f[k - 2] + f[k - 3]
                // 即在f[k - 1]左部继续查找k--，即下次循环mid = f[k - 1 - 1] - 1
                k--;
            } else if(key > temp[mid]) {
                // 全部元素 = 前面元素 + 后边元素 f[k] = f[k - 1] + f[k - 2]
                // 右边查找
                low = mid + 1;
                k -= 2;
            } else {
                return Math.min(mid, high);
            }
        }
        return -1;
    }
}

 

5、树表查找

　　5.1 最简单的树表查找算法——二叉树查找算法。

　　基本思想：二叉查找树是先对待查找的数据进行生成树，确保树的左分支的值小于右分支的值，然后在就行和每个节点的父节点比较大小，查找最适合的范围。 这个算法的查找效率很高，但是如果使用这种查找方法要首先创建树。 

　　二叉查找树（BinarySearch Tree，也叫二叉搜索树，或称二叉排序树Binary Sort Tree）或者是一棵空树，或者是具有下列性质的二叉树：

　　1）若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

　　2）若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

　　3）任意节点的左、右子树也分别为二叉查找树。

　　二叉查找树性质：对二叉查找树进行中序遍历，即可得到有序的数列。

        不同形态的二叉查找树如下图所示：

 

复杂度分析：它和二分查找一样，插入和查找的时间复杂度均为O(logn)，但是在最坏的情况下仍然会有O(n)的时间复杂度。原因在于插入和删除元素的时候，树没有保持平衡（比如，我们查找上图（b）中的“93”，我们需要进行n次查找操作）。我们追求的是在最坏的情况下仍然有较好的时间复杂度，这就是平衡查找树设计的初衷。

　　下图为二叉树查找和顺序查找以及二分查找性能的对比图：

 

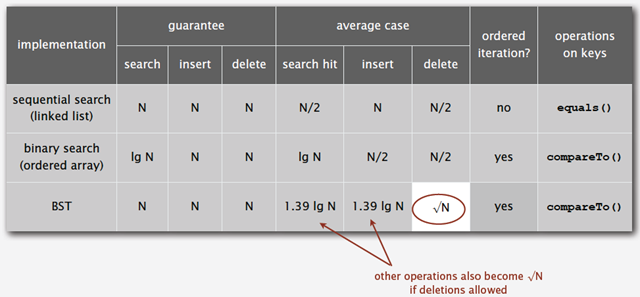
　　基于二叉查找树进行优化，进而可以得到其他的树表查找算法，如平衡树、红黑树等高效算法

 

二叉排序树的查找

public class BinarySearchTree {
    public static void main(String[] args) {
        // 主要是表达查询，所以手动构造一棵二叉排序树
        BinaryTree binaryTree1 = new BinaryTree();
        binaryTree1.data = 62;

        BinaryTree binaryTree2 = new BinaryTree();
        binaryTree1.lchild = binaryTree2;
        binaryTree2.data = 58;

        BinaryTree binaryTree3 = new BinaryTree();
        binaryTree2.lchild = binaryTree3;
        binaryTree3.data = 47;

        BinaryTree binaryTree4 = new BinaryTree();
        binaryTree3.lchild = binaryTree4;
        binaryTree4.data = 35;

        BinaryTree binaryTree5 = new BinaryTree();
        binaryTree4.rchild = binaryTree5;
        binaryTree5.data = 37;

        BinaryTree binaryTree6 = new BinaryTree();
        binaryTree3.rchild = binaryTree6;
        binaryTree6.data = 51;

        BinaryTree binaryTree7 = new BinaryTree();
        binaryTree1.rchild = binaryTree7;
        binaryTree7.data = 88;

        BinaryTree binaryTree8 = new BinaryTree();
        binaryTree7.lchild = binaryTree8;
        binaryTree8.data = 73;

        BinaryTree binaryTree9 = new BinaryTree();
        binaryTree7.rchild = binaryTree9;
        binaryTree9.data = 99;

        BinaryTree binaryTree10 = new BinaryTree();
        binaryTree9.lchild = binaryTree10;
        binaryTree10.data = 93;

        boolean search = serachBinaryTree(binaryTree1, 37, null);
        System.out.println(search == true ? "查找成功" + parentNode.data : "查找失败");
    }
    /**
     * 全局变量，存放查找到的关键字所在的父节点
     */
    static BinaryTree parentNode = new BinaryTree();

    /**
     * 二叉排序树
     * 
     * @param bt
     *            待查询的二叉排序树
     * @param key
     *            查找关键字
     * @param parent
     *            指向bt的双亲，其初始调用值为null
     * @return 查找成功返回true，并将树节点赋值给全局变量result，查找失败返回false
     */
    public static boolean serachBinaryTree(BinaryTree bt, int key, BinaryTree parent) {
        if (bt == null || bt.data == 0) { // 树节点不存在，返回
            parentNode = parent;
            return false;
        } else if (key == bt.data) { // 查找成功
            parentNode = bt;
            return true;
        } else if (key < bt.data) { // 关键字小于根节点查找左子树
            return serachBinaryTree(bt.lchild, key, bt);
        } else { // 关键字大于根节点查找右子树
            return serachBinaryTree(bt.rchild, key, parent);
        }
    }
    /**
     * 二叉树，数据结构
     * 
     */
    private static class BinaryTree {
        int data;
        BinaryTree lchild;
        BinaryTree rchild;
    }
}

二叉排序树插入操作

二叉排序树的插入，是将关键字放到树中的合适位置

package com.wzl.binary;

public class BinarySearchTree {
    public static void main(String[] args) {
        // 主要是表达查询，所以手动构造一棵二叉排序树
        BinaryTree binaryTree1 = new BinaryTree();
        binaryTree1.data = 62;

        BinaryTree binaryTree2 = new BinaryTree();
        binaryTree1.lchild = binaryTree2;
        binaryTree2.data = 58;

        BinaryTree binaryTree3 = new BinaryTree();
        binaryTree2.lchild = binaryTree3;
        binaryTree3.data = 47;

        BinaryTree binaryTree4 = new BinaryTree();
        binaryTree3.lchild = binaryTree4;
        binaryTree4.data = 35;

        BinaryTree binaryTree5 = new BinaryTree();
        binaryTree4.rchild = binaryTree5;
        binaryTree5.data = 37;

        BinaryTree binaryTree6 = new BinaryTree();
        binaryTree3.rchild = binaryTree6;
        binaryTree6.data = 51;

        BinaryTree binaryTree7 = new BinaryTree();
        binaryTree1.rchild = binaryTree7;
        binaryTree7.data = 88;

        BinaryTree binaryTree8 = new BinaryTree();
        binaryTree7.lchild = binaryTree8;
        binaryTree8.data = 73;

        BinaryTree binaryTree9 = new BinaryTree();
        binaryTree7.rchild = binaryTree9;
        binaryTree9.data = 99;

        BinaryTree binaryTree10 = new BinaryTree();
        binaryTree9.lchild = binaryTree10;
        binaryTree10.data = 93;

        insertBinaryTree(binaryTree1, 68);
    }

    /**
     * 全局变量，存放查找到的关键字所在的父节点
     */
    static BinaryTree parentNode = new BinaryTree();

    /**
     * 二叉排序树
     * 
     * @param bt
     *            待查询的二叉排序树
     * @param key
     *            查找关键字
     * @param parent
     *            指向bt的双亲，其初始调用值为null
     * @return 查找成功返回true，并将树节点赋值给全局变量result，查找失败返回false
     */
    public static boolean serachBinaryTree(BinaryTree bt, int key, BinaryTree parent) {
        if (bt == null || bt.data == 0) { // 树节点不存在，返回
            parentNode = parent;
            return false;
        } else if (key == bt.data) { // 查找成功
            parentNode = bt;
            return true;
        } else if (key < bt.data) { // 关键字小于根节点查找左子树
            return serachBinaryTree(bt.lchild, key, bt);
        } else { // 关键字大于根节点查找右子树
            return serachBinaryTree(bt.rchild, key, parent);
        }
    }

    /**
     * 在二叉树中插入关键字key
     * 
     * @param bt
     *            二叉排序树
     * @param key
     *            插入的关键字
     * @return 插入成功返回true，失败返回false
     */
    public static boolean insertBinaryTree(BinaryTree bt, int key) {
        BinaryTree binaryTree;
        if (!serachBinaryTree(bt, key, null)) {
            binaryTree = new BinaryTree();
            binaryTree.data = key;
            binaryTree.lchild = binaryTree.rchild = null;
            if (null == parentNode) {// 不存在，证明是父节点，将binaryTree指向bt成为新的根节点
                bt = binaryTree;
            } else if (key < parentNode.data) { // 当key小于子根节点，插入为左孩子
                parentNode.lchild = binaryTree;
            } else { // 当key大于子根节点，插入为右孩子
                parentNode.rchild = binaryTree;
            }

            preOrderTraverse(bt);
            return true;
        } else {
            System.out.println("该节点已存在");
        }

        return false;
    }
    /**
     * 中序遍历打印线索二叉树
     * 
     * @param t
     */
    static void preOrderTraverse(BinaryTree t) {
        if (null == t || t.data == 0) {
            return;
        }
        if (t.lchild != null) {
            preOrderTraverse(t.lchild); // 中序遍历左子树
        }
        if (t.data != 0) {
            System.out.println("[" + t.data + "]"); // 显示当前节点的数据
        }

        if (t.rchild != null) {
            preOrderTraverse(t.rchild); // 最后遍历右子树
        }
    }

    /**
     * 二叉树，数据结构
     * 
     */
    private static class BinaryTree {
        int data;
        BinaryTree lchild;
        BinaryTree rchild;
    }
}

二叉排序树的构建

package com.wzl.binary;

public class BinarySearchTree {
    public static void main(String[] args) {
        int[] a = { 62, 88, 58, 47, 35, 73, 51, 99, 37, 93 };  
        for (int i = 0; i < a.length; i++) {  
            System.out.println("第" + i+"次");  
            generateBinaryTree(a[i]);  
        }  

    }

     static BinaryTree newTree = new BinaryTree();  

    /**
     * 全局变量，存放查找到的关键字所在的父节点
     */
    static BinaryTree parentNode = new BinaryTree();

    /**
     * 二叉排序树
     * 
     * @param bt
     *            待查询的二叉排序树
     * @param key
     *            查找关键字
     * @param parent
     *            指向bt的双亲，其初始调用值为null
     * @return 查找成功返回true，并将树节点赋值给全局变量result，查找失败返回false
     */
    public static boolean serachBinaryTree(BinaryTree bt, int key, BinaryTree parent) {
        if (bt == null || bt.data == 0) { // 树节点不存在，返回
            parentNode = parent;
            return false;
        } else if (key == bt.data) { // 查找成功
            parentNode = bt;
            return true;
        } else if (key < bt.data) { // 关键字小于根节点查找左子树
            return serachBinaryTree(bt.lchild, key, bt);
        } else { // 关键字大于根节点查找右子树
            return serachBinaryTree(bt.rchild, key, parent);
        }
    }

    /**
     * 生成二叉树
     * @param key
     * @return
     */
    public static boolean generateBinaryTree(int key) {
        BinaryTree binaryTree;
        if (!serachBinaryTree(newTree, key, null)) {
            binaryTree = new BinaryTree();
            binaryTree.data = key;
            binaryTree.lchild = binaryTree.rchild = null;
            if (null == parentNode) {// 不存在，证明是父节点，将binaryTree指向bt成为新的根节点
                newTree = binaryTree;
            } else if (key < parentNode.data) { // 当key小于子根节点，插入为左孩子
                parentNode.lchild = binaryTree;
            } else { // 当key大于子根节点，插入为右孩子
                parentNode.rchild = binaryTree;
            }
            preOrderTraverse(newTree);
            return true;
        } else {
            System.out.println("该节点已存在");
        }

        return false;
    }
    /**
     * 中序遍历打印线索二叉树
     * 
     * @param t
     */
    static void preOrderTraverse(BinaryTree t) {
        if (null == t || t.data == 0) {
            return;
        }
        if (t.lchild != null) {
            preOrderTraverse(t.lchild); // 中序遍历左子树
        }
        if (t.data != 0) {
            System.out.println("[" + t.data + "]"); // 显示当前节点的数据
        }

        if (t.rchild != null) {
            preOrderTraverse(t.rchild); // 最后遍历右子树
        }
    }

    /**
     * 二叉树，数据结构
     * 
     */
    private static class BinaryTree {
        int data;
        BinaryTree lchild;
        BinaryTree rchild;
    }

}

5.2 平衡查找树之2-3查找树（2-3 Tree）

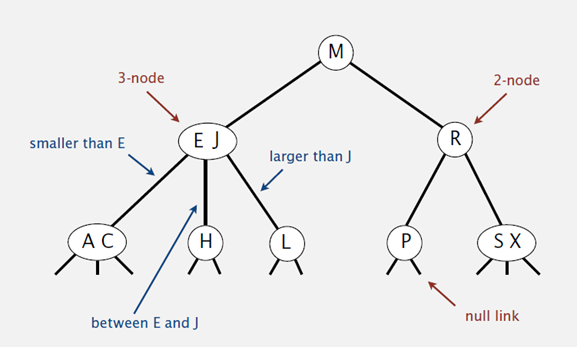
　　2-3查找树定义：和二叉树不一样，2-3树运行每个节点保存1个或者两个的值。对于普通的2节点(2-node)，他保存1个key和左右两个自己点。对应3节点(3-node)，保存两个Key，2-3查找树的定义如下：

　　1）要么为空，要么：

　　2）对于2节点，该节点保存一个key及对应value，以及两个指向左右节点的节点，左节点也是一个2-3节点，所有的值都比key要小，右节点也是一个2-3节点，所有的值比key要大。

　　3）对于3节点，该节点保存两个key及对应value，以及三个指向左中右的节点。左节点也是一个2-3节点，所有的值均比两个key中的最小的key还要小；中间节点也是一个2-3节点，中间节点的key值在两个跟节点key值之间；右节点也是一个2-3节点，节点的所有key值比两个key中的最大的key还要大。

2-3查找树的性质：

　　1）如果中序遍历2-3查找树，就可以得到排好序的序列；

　　2）在一个完全平衡的2-3查找树中，根节点到每一个为空节点的距离都相同。（这也是平衡树中“平衡”一词的概念，根节点到叶节点的最长距离对应于查找算法的最坏情况，而平衡树中根节点到叶节点的距离都一样，最坏情况也具有对数复杂度。）

　　性质2）如下图所示：

 

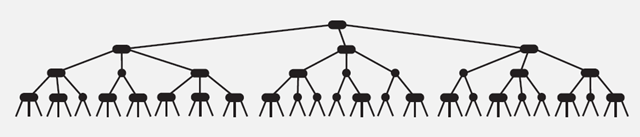
复杂度分析：

　　2-3树的查找效率与树的高度是息息相关的。

• 在最坏的情况下，也就是所有的节点都是2-node节点，查找效率为lgN
• 在最好的情况下，所有的节点都是3-node节点，查找效率为log3N约等于0.631lgN

　　距离来说，对于1百万个节点的2-3树，树的高度为12-20之间，对于10亿个节点的2-3树，树的高度为18-30之间。

　　对于插入来说，只需要常数次操作即可完成，因为他只需要修改与该节点关联的节点即可，不需要检查其他节点，所以效率和查找类似。下面是2-3查找树的效率：

　

5.3 平衡查找树之红黑树（Red-Black Tree）

　　2-3查找树能保证在插入元素之后能保持树的平衡状态，最坏情况下即所有的子节点都是2-node，树的高度为lgn，从而保证了最坏情况下的时间复杂度。但是2-3树实现起来比较复杂，于是就有了一种简单实现2-3树的数据结构，即红黑树（Red-Black Tree）。

　　基本思想：红黑树的思想就是对2-3查找树进行编码，尤其是对2-3查找树中的3-nodes节点添加额外的信息。红黑树中将节点之间的链接分为两种不同类型，红色链接，他用来链接两个2-nodes节点来表示一个3-nodes节点。黑色链接用来链接普通的2-3节点。特别的，使用红色链接的两个2-nodes来表示一个3-nodes节点，并且向左倾斜，即一个2-node是另一个2-node的左子节点。这种做法的好处是查找的时候不用做任何修改，和普通的二叉查找树相同。

 

 

　　红黑树的定义：

　　红黑树是一种具有红色和黑色链接的平衡查找树，同时满足：

• 红色节点向左倾斜
• 一个节点不可能有两个红色链接
• 整个树完全黑色平衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同。

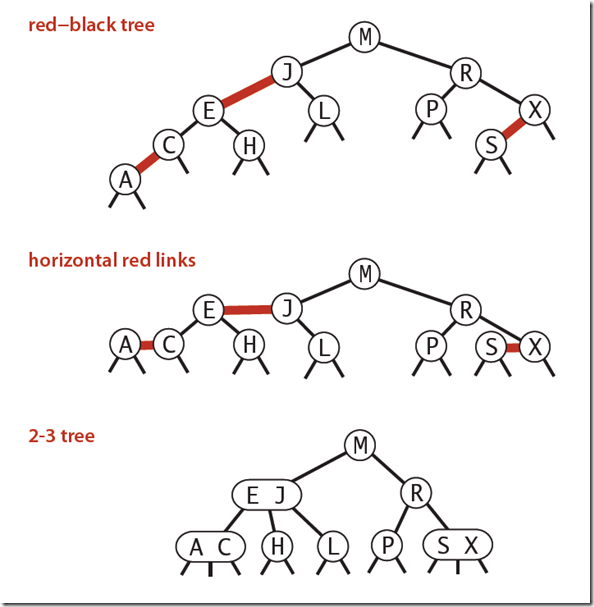
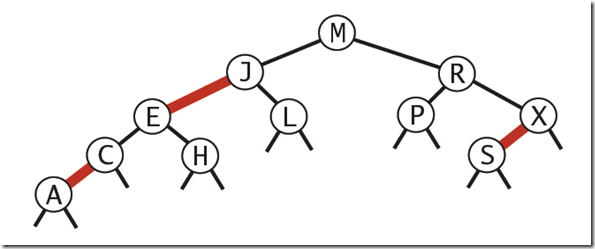
　　下图可以看到红黑树其实是2-3树的另外一种表现形式：如果我们将红色的连线水平绘制，那么他链接的两个2-node节点就是2-3树中的一个3-node节点了。

 

红黑树的性质：整个树完全黑色平衡，即从根节点到所以叶子结点的路径上，黑色链接的个数都相同（2-3树的第2）性质，从根节点到叶子节点的距离都相等）。咋·    

　　复杂度分析：最坏的情况就是，红黑树中除了最左侧路径全部是由3-node节点组成，即红黑相间的路径长度是全黑路径长度的2倍。

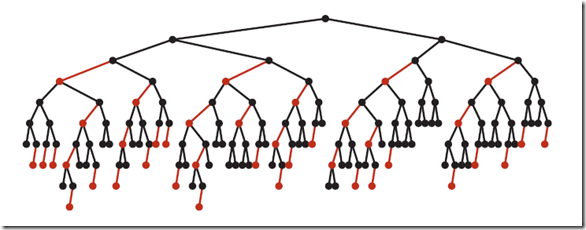
　　下图是一个典型的红黑树，从中可以看到最长的路径(红黑相间的路径)是最短路径的2倍：

红黑树的平均高度大约为logn。

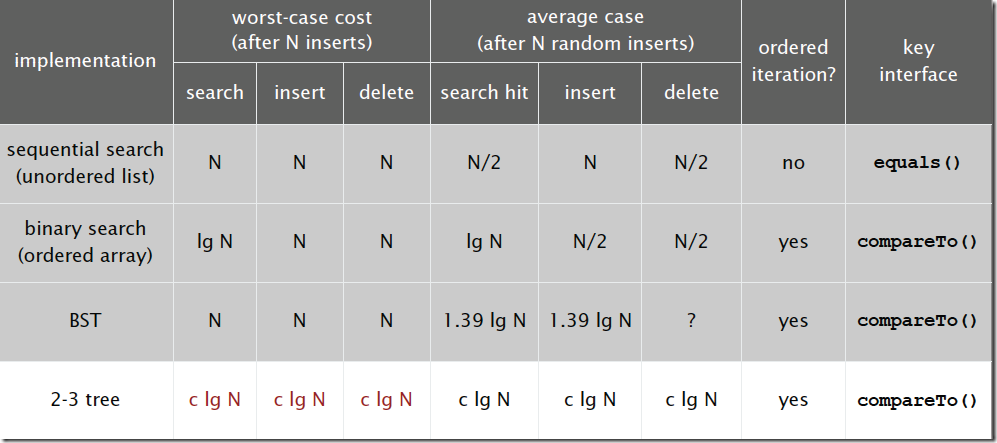
　　下图是红黑树在各种情况下的时间复杂度，可以看出红黑树是2-3查找树的一种实现，它能保证最坏情况下仍然具有对数的时间复杂度。

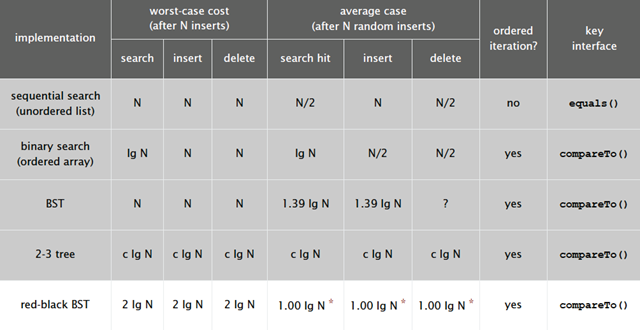
红黑树定义：

满足下列条件的二叉树是红黑树：

红链接均为左链接
没有任何一个结点同时和两条红链接相连
该树完美黑色平衡，即任意叶结点到根结点的路径上的黑链接数量相同

 

红黑树（RBT）基本结点

package Tree;

public class RBT<Key, Value> {

    private static final boolean RED = true;
    private static final boolean BLACK = false;
    private class Node {
        Key key;
        Value val;
        Node left, right;
        int N;
        boolean color;

        Node(Key key, Value val, int N, boolean color) {
            this.key = key;
            this.val = val;
            this.N = N;
            this.color = color;
        }
    }

    private boolean isRed(Node x) {
        if (x == null)
            return false;
        return x.color == RED;
    }
}

RED结点左右旋转

  private Node rotateLeft(Node h) {
        Node x = h.right;
        h.right = x.left;
        x.left = h;
        x.color = h.color;
        h.color = RED;
        x.N = h.N;
        h.N = size(h.left) + size(h.right) + 1;
        return x;
    }

    private Node rotateRight(Node h) {
        Node x = h.left;
        h.left = x.right;
        x.right = h;
        x.color = h.color;
        h.color = RED;
        x.N = h.N;
        h.N = h.left.N + h.right.N + 1;
        return x;
    }

    private void flipColors(Node h) {
        h.color = RED;
        h.left.color = BLACK;
        h.right.color = BLACK;
    }