1、基本概念
堆分为小根堆和大根堆,对于一个小根堆,它是具有如下特性的一棵完全二叉树:
(1)若树根结点存在左孩子或右孩子,则根结点的值(或某个域的值)小于等于左右孩子结点的值(或某个域的值)
(2)以左、右孩子为根的子树又各是一个堆。
大根堆的定义将上面的小于等于改成大于等于即可。
根据根的定义,小根堆的堆顶结点具有最小值,大根堆的堆顶结点具有最大值。
2、堆的存储结构
由于堆是一棵完全二叉树,所以适宜采用顺序存储结构,这样能够充分利用存储空间。
顺序存储结构:
对堆中所有结点进行编号,作为下标存储到指定数组的对应元素中,下标从0开始。按照从上到下,同一层从左到右进行。
设堆中有n个结点,则编号为 0 ~ n-1,则有如下性质:
(1)编号为 0 至 [n/2-1] 的结点为分支结点, 编号为 [n/2] 至 n-1 的结点为叶子结点;
(2)当 n 为奇数则每个分支结点既有左孩子又有右孩子,当 n 为偶数则每个分支结点只有左孩子没有右孩子
(3)对于每个编号为 i 的分支结点,其左孩子结点的编号为 2i+1,右孩子结点的编号为 2i+2
(4)除编号为0的堆顶结点外,对于其余编号为 i 的结点,其双亲结点的编号为 [(i-1)/2]
下图为一个堆及其顺序存储结构
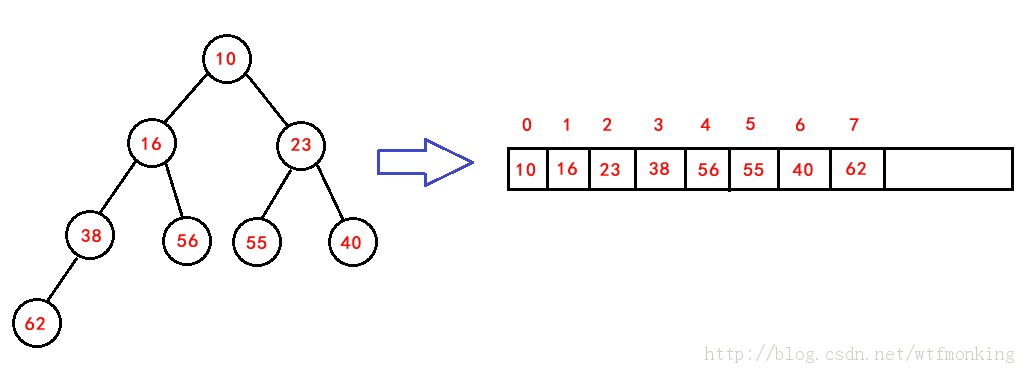
3、堆的操作及运算
用如下程序详细展示堆的操作及运算,程序之后将还会有详细的讲解操作过程的实现原理。
#include<stdio.h> #include<stdlib.h> typedef int ElemType; struct HeapSq //定义堆的顺序存储类型 { ElemType* heap; //定义指向动态数组空间的指针 int len; //定义保存堆长度的变量,即数组长度,数组下标从0开始 int MaxSize; //用于保存初始化时所给的动态数组空间的大小 }; //1、初始化堆 void InitHeap(struct HeapSq* HBT, int MS) { if (MS <= 0) { printf("数组长度参数不合适,需重新给定! "); exit(1); } HBT->heap = malloc(MS*sizeof(ElemType)); if (!HBT->heap) { printf("用于动态分配的内存空间用完,退出运行! "); exit(1); } HBT->MaxSize = MS; HBT->len = 0; } //2、清除堆 void ClearHeap(struct HeapSq* HBT) { if (HBT->heap != NULL) { free(HBT->heap); HBT->len = 0; HBT->MaxSize = 0; } } //3、检查一个堆是否为空 int EmptyHeap(struct HeapSq* HBT) { if (HBT->len == 0) return 1; else return 0; } //4、向堆中插入一个元素 void InsertHeap(struct HeapSq* HBT, ElemType x) { int i; if (HBT->len == HBT->MaxSize) //若堆满,将数组空间扩展为原来的2倍 { ElemType *p; p = realloc(HBT->heap, 2*HBT->MaxSize*sizeof(ElemType)); if (!p) { printf("存储空间用完! "); exit(1); } printf("存储空间已扩展为原来的2倍! "); HBT->heap = p; HBT->MaxSize = 2*HBT->MaxSize; } HBT->heap[HBT->len] = x; //向堆尾添加新元素 HBT->len++; //堆长度加1 i = HBT->len - 1; //i指向待调整元素的位置,即其数组下标,初始指向新元素所在的堆尾位置 while (i != 0) { int j = (i - 1) / 2; //j指向下标为i的元素的双亲 if (x >= HBT->heap[j]) //若新元素大于待调整元素的双亲,则比较调整结束,退出循环 break; HBT->heap[i] = HBT->heap[j]; //将双亲元素下移到待调整元素的位置 i = j; //使待调整位置变为其双亲位置,进行下一次循环 } HBT->heap[i] = x;//把新元素调整到最终位置 } //5、从堆中删除堆顶元素并返回 ElemType DeleteHeap(struct HeapSq* HBT) { ElemType temp, x; int i, j; if (HBT->len == 0) { printf("堆已空,退出运行! "); exit(1); } temp = HBT->heap[0]; //暂存堆顶元素 HBT->len--; if (HBT->len == 0) //若删除操作后堆为空则返回 return temp; x = HBT->heap[HBT->len]; //将待调整的原堆尾元素暂存x中,以便放入最终位置 i = 0; //用i指向待调整元素的位置,初始指向堆顶位置 j = 2 * i + 1;//用j指向i的左孩子位置,初始指向下标为1的位置 while (j <= HBT->len - 1)//寻找待调整元素的最终位置,每次使孩子元素上移一层,调整到孩子为空时止 { if (j < HBT->len - 1 && HBT->heap[j] > HBT->heap[j+1])//若存在右孩子且较小,使j指向右孩子 j++; if (x <= HBT->heap[j]) //若x比其较小的孩子还小,则调整结束,退出循环 break; HBT->heap[i] = HBT->heap[j];//否则,将孩子元素移到双亲位置 i = j; //将待调整位置变为其较小的孩子位置 j = 2 * i + 1;//将j变为新的待调整位置的左孩子位置,继续下一次循环 } HBT->heap[i] = x; //把x放到最终位置 return temp; //返回原堆顶元素 } //主函数 void main() { int i, x; int a[8] = {23,56,40,62,38,55,10,16}; struct HeapSq b; InitHeap(&b, 10); for (i = 0; i < 8; i++) InsertHeap(&b, a[i]); while (!EmptyHeap(&b)) //依次删除堆顶元素并显示出来,直到堆空为止 { x = DeleteHeap(&b); printf("%d", x); if (!EmptyHeap(&b)) printf(","); } printf(" "); system("pause"); ClearHeap(&b); }
运行结果:

分析:
(1)讲下堆的插入操作:
向堆中插入一个元素时,首先将该元素写入到堆尾,即堆中最后一个元素后面(下标为 len 的位置上),然后调整为一个新堆。
调整方法:若新元素小于双亲结点的值,就让它们互换位置,新元素换到双亲位置后,使得以该位置为根的子树称为堆;
然后再对该位置与其双亲结点的值比较,做同样的调整,直到以新位置的双亲结点为根仍是一个堆,或者调整到堆顶为止,此时整个树变称为了一个堆。
上面的程序,依次将数组[23,56,40,62,38,55,10,16]的中的元素插入堆,插入过程如下:

我们拿其中一个步骤具体分析,比如插入最后一个元素16时,插入之前的示意图为上图中的倒数第二个图,在此图的基础上,将16插入堆尾,即62的左孩子位置,
此时16比其双亲62小,则使其与62互换位置,而此时16又比它所处的新位置的双亲38小,则再与38互换,最后此时16比它所处的新位置的双亲10大,则调整结束,
最后结果即为上图中的最后一个图所示。
(2)讲下堆的删除操作
删除操作是删除堆顶元素,留下的堆顶位置由堆尾位置填补,然后将其调整为一个新堆,
调整方法:新的堆顶元素值若大于两个孩子结点中的最小值,就将它与具有最小值的孩子结点互换位置,
在被换到孩子结点位置后,再对此位置与其孩子结点最小值比较,进行同样的调整,
直到以调整后的位置为根的子树称为一个堆,或者调整到叶子结点为止。
上面的程序依次删除堆顶元素的过程如下:
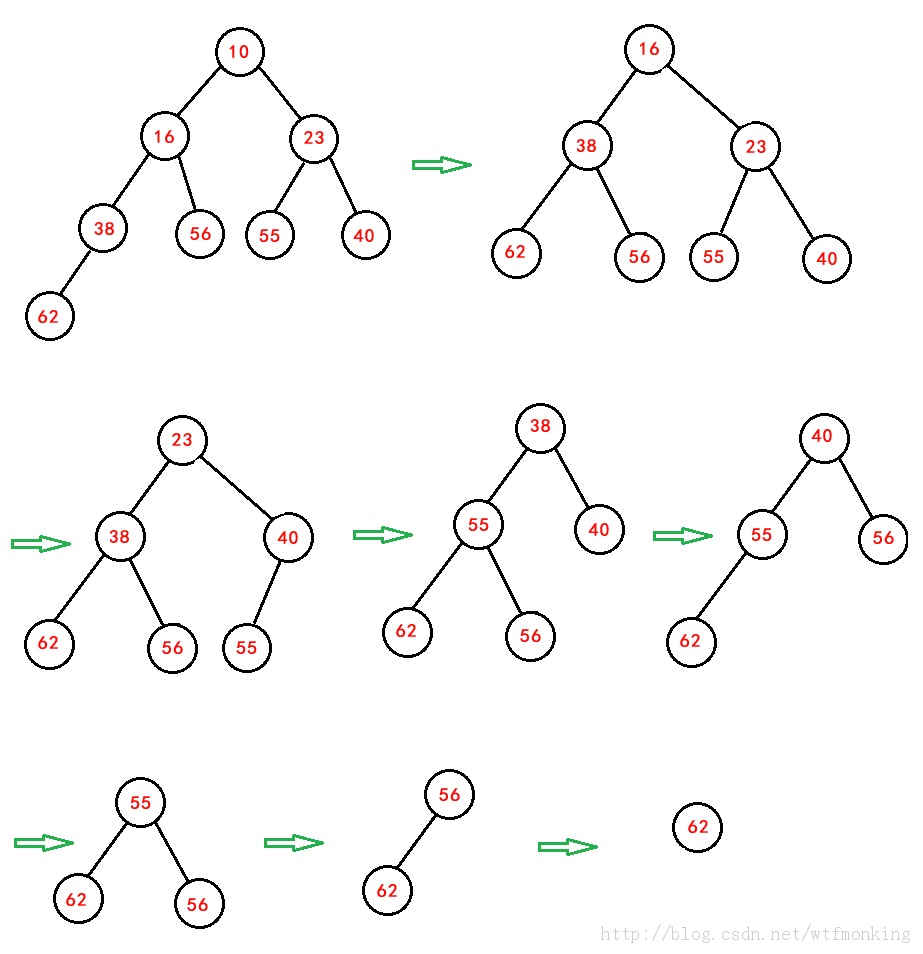
我们拿其中一个具体分析,如删除第一个堆顶元素10时,删除之前的示意图为上图中的第一个图,在此图的基础上,将10删除,然后将堆尾元素62放在堆顶,
此时,62比其所在位置的孩子的最小值16大,则将其与16位置互换,而此时62又比其所在位置的孩子的最小值38大,则将其与38位置互换,此时的62所在的位置是
叶子结点,调整结束,最后的结果为上图中的第二个图所示。