6.1. 问题描述
6174数字黑洞是印度数学家卡普雷卡尔于1949年发现的,又称为卡普雷卡尔黑洞,其规则描述如下。
任意取一个4位的整数(4个数字不能完全相同),把4个数字由大到小排列成一个大的数,又由小到大排列成一个小的数,再把两数相减得到一个差值。之后对这个差值重复前面的变换步骤,经过若干次重复就会得到6174。
例如,对整数8848按规则进行变换操作,其过程如下。
- 重排取大数:将8848的4个数字按从大到小排列组成一个最大数8884。
- 重排取小数:将8848的4个数字按从小到大排列组成一个最小数4888。
- 求取差值:用大数减去小数得到差值3996。
- 重复变换:之后对差值继续按上述步骤进行变换。操作的过程为:
9963-3699=6264
6642-2466=4176
7641-1467=6174。
经过4次变换之后,就将自然数8848变换为6174这个黑洞数字,并且继续变换也会一直是6174。
请编写一个程序,验证卡普雷卡尔黑洞。
6.2. 算法分析
在程序设计中,当解决复杂问题时,通常采用“自顶向下,逐步求精”的模块化设计思想,将一个复杂的任务逐层分解为若干个功能单一的子任务,如果某个子任务仍然复杂,还可以继续分解为更小的子任务,直到每个子任务简单明了。简单地说就是,化整为零,各个击破。
面对编程验证卡普雷卡尔黑洞这个任务,根据其规则描述,可分解为输入数字、检测数字合法性、黑洞变换3个子任务。其中,黑洞变换这个子任务稍显复杂,又可以划分出分解数字、取大数、取小数这3个较小的子任务。分解后的各个子任务呈现为一个树状结构,可以使用功能结构图来表示,如图14-1所示。
经过分解,各个子任务已经足够简单。每个子任务称为一个功能模块,能够单独进行设计、编码和测试。各功能模块的实现步骤描述如下。
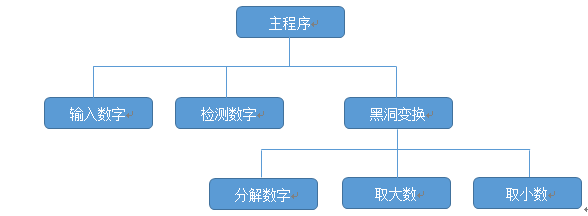
在上图中,主程序之下有三个模块,主程序先调用输入数字模块接收用户通过键盘输入的一个整数,再调用检测数字模块检测这个整数是否合法。如果检测通过,调用黑洞变换模块进行数字变换操作;否则,提示“输入的整数不合法”,并结束程序。
主程序模块流程图如下:
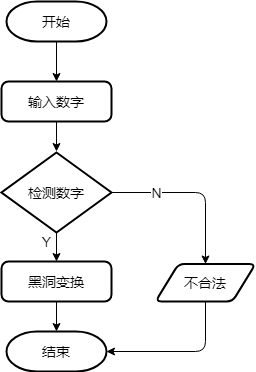
至于其他子模块的流程图,这里不再给出,有兴趣的童鞋可以去原书《Python趣味编程:从入门到人工智能》查看。
6.3. 编程解题
在上述算法分析中,采用“自顶向下,逐步求精”的模块化设计思想,将验证数字黑洞的任务分解为多个小的功能模块,每个模块功能单一,易于编程实现。我们来看看python程序怎么实现:
1 ''' 2 程序:卡普雷卡尔黑洞,6174数字黑洞 3 作者:苏秦@小海豚科学馆公众号 4 来源:图书《Python趣味编程:从入门到人工智能》 5 ''' 6 #主程序 7 def main(): 8 n = input('请输入4位数字不完全相同的整数:') 9 if check(n): 10 blackhole(n) 11 else: 12 print('输入的整数不合法') 13 14 #检测数字 15 def check(n): 16 if not n.isnumeric(): 17 return False 18 elif len(n) != 4: 19 return False 20 elif n == n[0] * 4: 21 return False 22 else: 23 return True 24 25 #黑洞变换 26 def blackhole(n): 27 print('变换过程:') 28 while n != '6174': 29 a = list(n) 30 b = max_number(a) 31 c = min_number(a) 32 n = str(b - c) 33 print('%s - %s = %s' % (b, c, n)) 34 print('变换结束!') 35 36 #取大数 37 def max_number(a): 38 a.sort(reverse=True) 39 num = int(''.join(a)) 40 return num 41 42 #取小数 43 def min_number(a): 44 a.sort() 45 num = int(''.join(a)) 46 return num 47 48 #程序入口 49 if __name__ == '__main__': 50 main()
从上面的代码可以看出,“检测数字”等模块被定义成了独立的代码块,这就是python的自定义函数,通常它是这个样子的:

其中如果不需要参数,函数名后面的括号可以留空,多个参数用逗号(,)隔开。
现在我们把上面的python代码转换成julia代码:
1 #= 2 程序:卡普雷卡尔黑洞,6174数字黑洞 3 作者:苏秦@小海豚科学馆公众号 4 来源:图书《Python趣味编程:从入门到人工智能》 5 =# 6 "主程序" 7 function main() 8 n = input("请输入4位数字不完全相同的整数:") 9 if check(n) 10 blackhole(n) 11 else 12 print("输入的整数不合法") 13 end 14 end 15 16 #检测数字 17 function check(n) 18 #= 19 julia中没有判断字符串是否为数字的内置函数 20 只能用这种方式实现了。(isnumeric,isdigit 21 函数的参数都是字符不是字符串) 22 =# 23 if tryparse(Int, n)===nothing 24 return false 25 elseif length(n) != 4 26 return false 27 elseif n == repeat(n[1],4) 28 return false 29 else 30 return true 31 end 32 end 33 34 #黑洞变换 35 function blackhole(n) 36 println("变换过程:") 37 while n != "6174" 38 a = split(n,"") 39 b = max_number(a) 40 c = min_number(a) 41 n = string(b - c) 42 #julia的参数字符串比python简洁些 43 println("$b - $c = $n") 44 end 45 print("变换结束!") 46 end 47 48 #取大数 49 function max_number(a) 50 a=sort(a,rev=true) 51 #将数组元素组合成字符串 52 num=parse.(Int,join(a,"")) 53 return num 54 end 55 56 #取小数 57 function min_number(a) 58 a=sort(a) 59 num=parse.(Int,join(a,"")) 60 return num 61 end 62 63 """ 64 #这是重写的实现类似Python的input函数 65 参数:string类型,默认值为空 66 返回值:string类型 67 """ 68 function input(prompt::String="")::String 69 print(prompt) 70 return chomp(readline()) 71 end 72 main()
从上面的代码中我们可以看出,julia的自定义函数的格式是这样的:

同样的,如果不需要参数,函数名后面的括号可以留空,多个参数用逗号(,)隔开。另外参数可以定义类型和默认值,函数可以定义返回值类型等。例如:
function input(prompt::String="")::String
另外,大家可能发现上面的python和julia代码中都有一个main函数,而且python还有“if __name__ == '__main__':”这种写法。事实上,与C、C++、java等静态语言强制使用main函数作为程序入口函数不同的是,python其实是没有main函数的,这里使用main函数作为程序的起始,只是一种结构化编程的方式,同理,julia也一样。当然,python中“if __name__ == '__main__':”使得名称为main的函数体中的代码语句,只能在当前文件被单独运行的时候被执行,如果当前python文件被作为外部模块引用的时候,main还是中的代码语句不会被执行,所以,通常会把一些测试类的代码写在main函数里面。当然,作为工程化开发时,不建议这样做,测试代码应该写到单独的文件中去。
这里有必要说一下julia的代码注释,Julia自v0.4版本之后,便提供了内置的文档注释系统,可以很方便地对函数、类型、对象及语句进行描述,直接支持Markdown格式[[1]],能够生成非常实用、方便的说明文档。
最简单的注释是一句话就可说清楚的单行注释方式,以井号#作为注释内容的前缀,一般放于语句的上一行或当前行尾部。请参考上面的代码,此处不再赘述。
对于多行注释,一般在注释内容的上下行使用#=与=#两个标记符进行界定,请参考上面代码的开头的程序、作者声明。
另外,类型声明、函数与宏定义等上一行中单独出现的字符串对象都会被认为是注释内容,上面main函数的注释就是这样的。当然,多行字符串也是支持的,而且遵循Markdown语法格式。请参看上面input函数的注释。