学数数



in
3 5
1 2 3
> 1
< 2
= 3
> 4
< 5
out
5
1
3
0
6

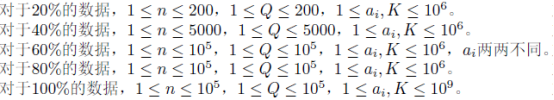
分析:
其实我觉得我最大的问题就是把这题定死了是线段树,虽然说线段树也可以,因为这题只是利用它维护前缀和的功能,但更应该去思考的是如何整合这三种询问,并用一种好的方法解决问题。很显然的,对于三种询问可以只维护<的情况来表示三种情况,其中=为x-(x-1),意会一下;>只要知道题目说的总数为(n+1)*n/2就很好解决了。接着对于答案的求解,我们很显然可以发现一个数对答案的贡献与其左端和右端 第一个比它大(或等于)的数有关,当然为防止重复计数我们要规定一下左端是严格大于,右端是大于等于(可以自己列几个重复数字玩玩),这样贡献就是(左端数个数+本身)*(右端数个数+本身)。至于如何求左右两边比它大的数,可以用单调栈扫一遍。
代码:
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #include<queue> #include<algorithm> #include<vector> using namespace std; #define debug printf("zjyvegetable ") #define int long long #define mid ((l+r)>>1) #define lp (p<<1) #define rp (p<<1|1) inline int read(){ int a=0,b=1;char c=getchar(); while(!isdigit(c)){if(c=='-')b=-1;c=getchar();} while(isdigit(c)){a=a*10+c-'0';c=getchar();} return a*b; } const int N=2e5+50,M=4e6+50; int n,q,m,total,top,a[N],b[N],sta[N],l[N],r[N],sum[N]; int lowbit(int x){ return x&-x; } void putin(int k,int z){ for(;k<=m;k+=lowbit(k)){ sum[k]+=z; } } int query(int k){ int ans=0; for(;k;k-=lowbit(k)) ans+=sum[k]; return ans; } signed main(){ freopen("jxthree.in","r",stdin); freopen("jxthree.out","w",stdout); n=read();q=read(); total=(n+1)*n/2; for(int i=1;i<=n;i++) a[i]=b[i]=read(); sort(b+1,b+n+1); m=unique(b+1,b+n+1)-b-1; for(int i=1;i<=n;i++){ a[i]=lower_bound(b+1,b+m+1,a[i])-b; } for(int i=1;i<=n;i++){ r[i]=i+1; if(!top){ sta[++top]=i; } else{ while(top&&a[sta[top]]<a[i]){ r[sta[top]]=i; top--; } l[i]=sta[top]; sta[++top]=i; } } while(top){ r[sta[top]]=n+1; top--; } for(int i=1;i<=n;i++){ putin(a[i],(i-l[i])*(r[i]-i)); } char op[3];int u,v; for(int i=1;i<=q;i++){ scanf("%s",op);v=read(); u=lower_bound(b+1,b+m+1,v)-b; if(op[0]=='<')printf("%lld ",query(u-1)); else if(op[0]=='='){ if(b[u]!=v)printf("0 "); else printf("%lld ",query(u)-query(u-1)); } else{ if(b[u]!=v)u--; printf("%lld ",total-query(u>m?m:u)); } } return 0; }
最后:
其实对我来说,这题最大的收获是单调栈,主要是因为用的少,打上一遍后发现了很多细节和感受了单调栈的用处,算是收获满满吧。