偶感
偶尔开几个脑洞,别太认真~
你怎样理解序列化和反序列化?
答:我认为这就是广义的I/O,也就是以网络传输作为形式的文件读写操作。
大数据是什么?
答:大数据就是一场炒作,就是人懒得去分析表之间的关系,然后用machine learning,deep learning的各种算法去计算。实际上就是统计学+web程序设计+传感器采集数据,没什么高端的东西。
好吵
504有个人敲键盘,一直敲,好像在玩qq炫舞,烦死了!!!!!傻逼!!!
node.js
以前看node.js,纯粹是因为浮躁跟风,想了解最新的最潮的东西。那时候都不懂网络编程,不理解同步和异步,所以,看了也没啥用。要重新看了。
好吧,其实没看几页又扔了,因为用不到!小公司不要我!!
努力和聪明的区别
就像是在最一道acm题目,努力是什么,是你能够写出模拟程序,能够去遍历;而聪明,则是能理清问题中各种变量之间的关系,能更快解出答案,不用遍历而胜似遍历。如果体力太少,连遍历都做不到,那真的是没救了。所以说,以大多数人的努力程度之低,还轮不到拼天赋。
金融数据挖掘?
2015年8月9日 23:11:41
想到以前实习做金融数据挖掘,说要找模型看paper。我表示,在不了解有监督的分类以及回归的情况下,去看数据挖掘,去研究理财产品和用户数据,真是扯淡。不要上来就说模型,给出具体的几个算法名不好吗?knn,朴素贝叶斯,决策树,svm,然后是无监督的kmeans、EM,各种神经网络......总之以前太不了解行情了,如果那时候先自己看完了这些,再去实习,就真的能做出东西来了...问题是现在还有神经网络没有看!
test data
http://blog.snsgou.com/blog/161.html
http://mp.weixin.qq.com/wiki/12/2108cd7aafff7f388f41f37efa710204.html
卷积和map-reduce
2015年 10月 04日 星期日 00:17:21 CST
卷积操作是什么?在图像处理中,有一个小的矩阵(通常是奇数阶方阵),和图像矩阵中某一个区域,对应元素相乘,然后把所有乘积相加。
这其实就是一种很简单的map-reduce过程。看过SICP后就理解了(其实是看SICP前显然能够理解但是没有刻意去注意去理解:),map就是一个分布式处理操作,对序列中每个元素做同样的一个op操作;而reduce,或者在SICP中叫accumulate,是处理map后的所有结果的一个操作。
在卷积操作中,map操作是元素相乘,reduce操作是乘积累加。
当然,矩阵相乘也可以从map-reduce的角度去理解。其实谁不懂map-reduce呢?只不过现在分布式发展壮大了,map-reduce能真正大规模使用了,所以受到关注。
什么样的公式是好的公式?
以前初中高中物理有不少公式,以及各种变形。当时图省事,我把公式和公式变形都记的很熟,因为各种题目不会傻到直接套用公式,至少是公式变形一下,比如用原公式是用a、b变量计算出c,题目会给出a、c的值,让你求b的值。当时我对于公式的态度,原公式和变形公式几乎同样熟悉。这对于解题当然正确,但是思维上有问题。
什么样的公式是好公式?初中物理老师说过这些公式只要记住一个,会推导出其他公式,就可以了。那么这个用来推导其他公式的公式,就是好公式了。可是这还是没什么感觉。书本给出的公式,应该就是好公式了;而书本上给出的推论或者小字部分给出的公式,就不是好公式了。?
然而生活没有那么多课本给我们用,课本终有用光的一天,无论是职场还是科研,没有具体课本的时候我们怎样自己归纳总结公式?
显然,用已知的东西定义未知的东西,这是必须的,但仍然是不够的;用具体的,去定义抽象的,这才是需要的。这用来定义新概念的具体概念,也通常不会是具体物质形式存在的东西,而是抽象描述的、为你我所熟知的概念,是一种具体的“抽象”;而新定义的概念,是更加抽象一层的概念。同时,还应当保证,这用于定义新概念的概念,要精简而避免冗余;要尽量打包而不是最原始的概念。
好吧,这种想法其实就是欧几里得几何的公理化方法的一种延伸罢了,只不过现在对于所定义的概念,有了层级的区分:它们不是全都处于同级的,总有更加抽象的。
一个具体的例子:频率:单位时间内完成周期性变化的次数。这是一个好的定义。因为有两个抽象层级存在。
排序的本质
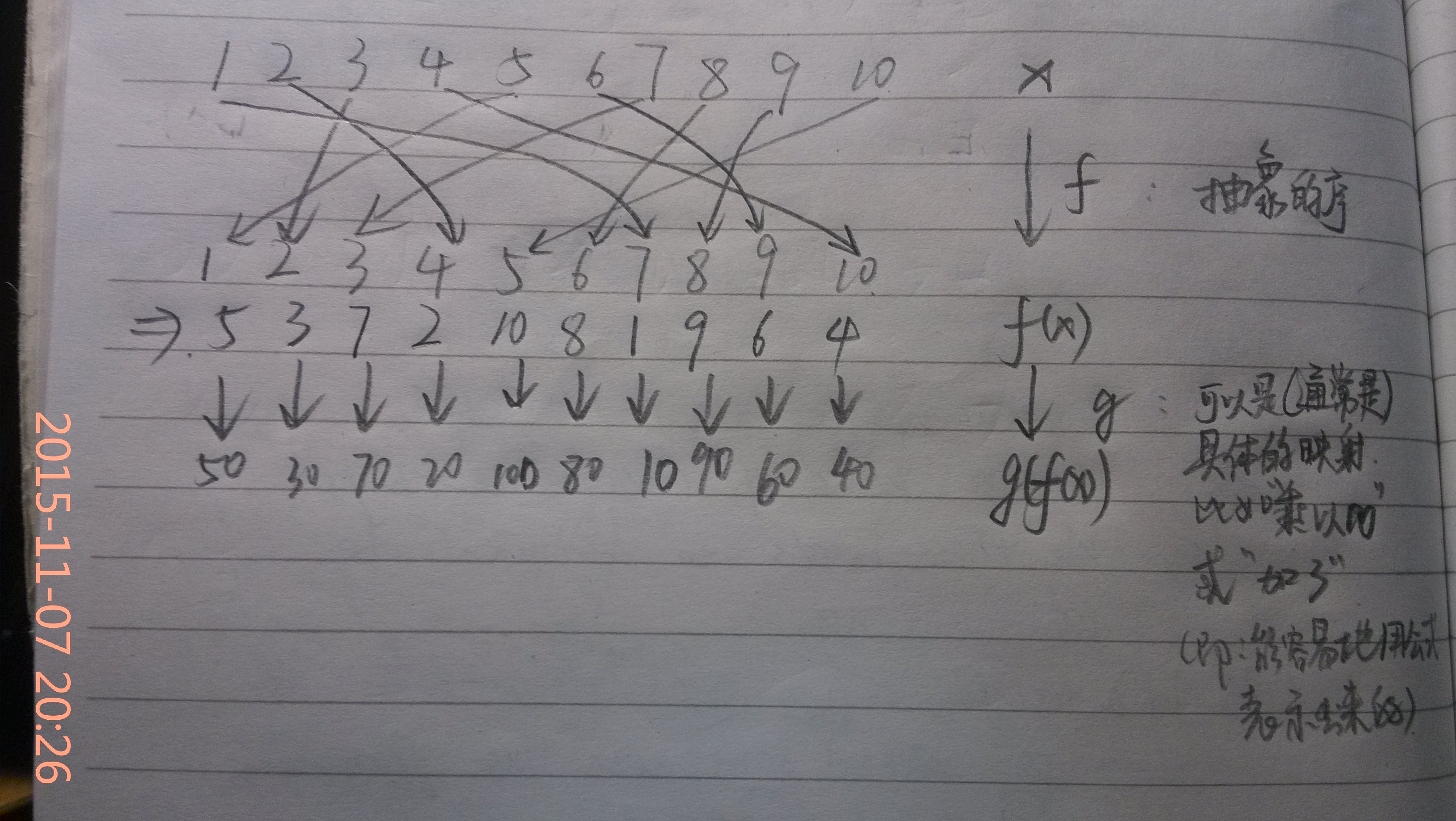
原有的有序元数据,因为某种原因被映射得到无序的数据。所谓排序,就是求从无序数据到有序数据的一个映射。
当然一般情况没这么简单,通常是:x -> f(x) -> g(f(x)) -> f(x) -> x
即:原始数据x被映射为f(x),这时候已经是乱序了;但是通常还需要套一层g映射,g一般是能具体写出函数表达式的映射(例如放大10倍,或者增加10。。貌似这就是尺度变换(缩放)和平移变换。。orz);然后,我们现实中往往是只有观测数据g(f(x)),要求取x的,这就需要先做g^(-1)映射,再做f^(-1)映射。
g^(-1)映射很简单(这里只考虑没有重复元素的排序问题),f^(-1)则很难,是排序的核心问题。因为往往得不到f^(-1)的具体表达式。
顺便说下,g^(-1)映射可以看成是离散化的过程。
直方图:一个map reduce的很容易理解的例子
接触过数字图像处理的人肯定知道直方图。
就算没有接触过数字图像处理,中学里也肯定学过频率分布直方图。
这个直方图的构建过程,就是一个map reduce的过程。
首先,你手头得到数据。这些数据是连续型数据(浮点数)。
然后你把他们离散化:每个数据划归到一个子区间内。比如区间长度为10,那么区间端点之间的数据都算这个区间的。这个就是一个map的过程。
然后你在map好的基础上,统计每个区间内的原始数据数量。这就是reduce过程。
好了,现在你得到每个区间的统计数据了,可以画直方图了。
真实世界的map reduce,无非是类似的任务分配给不同的机器去做(map),做好之后再汇总(reduce)。
额。。这里的reduce的理解有点问题,好像不对。。。挖坑待填。
遗传算法和社会流动性
遗传算法讲究一个基因突变率。突变率不能太高也不能没有。
社会人口结构也是类似的,要保证一定的流动性,不能太高也不能太低。。。。自适应和演化自适应。。。
但是社会的人口流动性不是一个人在控制,而且新的king上任后可能还会变化,远比遗传算法要复杂。。
从毕达哥拉斯想到的
古希腊,毕达哥拉斯学派,他们认为宇宙的everything都可以用数字表示(大概意思)。
其实显然这太偏执了。我的身体,我的手机,我的水杯,你说,哪个是纯数字?
但是里面的思想是有趣的,是有启发意义的。
这个世界上的人,可以认为是由一小撮精英和一大群普通人组成的。这群精英,可以认为是最重要部分。
其实可以考虑用n维向量来描述事物。没错,任何事物都可以用meta-description+特征向量的形式进行描述,而向量的每个元素都是数字。
这个世界,是向量的世界。而现在这个时代,人们都在找各种提取特征向量(提取feature)的方法。无监督方法代表未来。
真实世界可能并不存在太多的“平均值”
比如我在复习《计算理论基础》的13道复习题,我不可能复习完6.5道题目。就算题目是12道,难度也不一定相同;就算难度相同,我的状态也不一样,可能后面的几道题根本没有真的弄懂。。
There's no static mean value. I must surpass it, or I'll lost.
这或许就是“学如逆水行舟,不进则退”的一种表现形式吧。