几种回文算法的比较

前言

这是我的第一篇博文，献给算法。

学习和研究算法可以让人变得更加聪明。

算法的目标是以更好的方法完成任务。

更好的方法的具体指标是:

  1. 花费更少的执行时间。

  2. 花费更少的内存。

在对方法的不断寻找，对规律的不断探索中，个人的思考能力能够被加强。当敏捷的思考能力成为一种固有特征时，人就变得聪明起来。

研究算法其实是研究事物的规律。对事物的变化规律掌握的越准确、越细致、越深入，就能找到更好的算法。

在探索规律的过程当中，一定会经历失败。但是这种失败是值得的，因为它可以为解决其它问题提供基础。

回文算法: 

回文指从左往右和从由往左读到相同内容的文字。比如: aba，abba，level。

回文具有对称性。

回文算法的目标是把最长的回文从任意长度的文本当中寻找出来。比如：从123levelabc中寻找出level。

框架代码

框架代码包含除核心算法代码的所有其他部分代码。

1. main()函数，使用随机数产生10M长度的字符串。然后调用核心算法代码。

2. 时间函数，用于统计并比较不同算法耗时的差别。

#include <vector>
#include <iostream>
#include <string>
#include <minmax.h>
#include <time.h>
#include <Windows.h>
#include <random>
#include <assert.h>

using namespace std;

__int64 get_local_ft_time(){
    SYSTEMTIME st;
    __int64 ft;
    GetLocalTime(&st);
    SystemTimeToFileTime(&st, (LPFILETIME) &ft);
    return ft;
}

int diff_ft_time_ms(__int64 subtracted, __int64 subtraction){
    return (int)((subtracted - subtraction) / 10000);
}

int main() {
    int length = 1024 * 1024 * 10;
    LPSTR s = new char[length + 1];

    srand(time(NULL));
    for (int i = 0; i < length; i++){
        s[i] = (char) ((rand() % 26) + 'a');
    }

    palindrome_raw(s, length);
    Manacher(s, length);
    palindrome_zjs(s, length);

    delete [] s;
    //cin.get();
}

回文算法: 原始算法

原始算法指按照回文的原始定义，利用数据的对称性(s[i - x] = s[i + x])来寻找回文的算法。

void palindrome_raw(LPSTR t, int length) {
    cout << "palindrome_raw" << endl;
    __int64 start = get_local_ft_time();

    int max = 0;                                                  // 最长回文的起点
    int l_max = 1;                                                // 最长回文的长度(l: length, 长度的意思)
    for (int i = 1; i < length; i++) {                            // i为对称点
        int d = 1;                                                // d为回文扩展半径
        while (i - d >= 0 && i + d < length && 
               t[i - d] == t[i + d]){                             // 以i为中心对称。aba
            d++;
        }
        d--;
        if (2 * d + 1 > l_max){
            max   = i - d;
            l_max = 2 * d + 1;
        }
                                                                  // 循环结束时d总不满足判断条件，所以减1
        d = 0;                                                    // d为回文扩展半径
        while (i - d >= 0 && i + 1 + d < length && 
               t[i - d] == t[i + 1 + d]){                         // 以i后面空隙为中心对称。abba
            d++;
        }
        d--;
        if (2 * (d + 1) > l_max){
            max   = i - d;
            l_max = 2 * (d + 1);
        }
    }

    char c = t[max + l_max];
    t[max + l_max] = 0;
    cout << t + max << endl;
    t[max + l_max] = c;
    __int64 end = get_local_ft_time();
    cout << "处理时间: " << diff_ft_time_ms(end, start)  << "ms" << endl;
}

算法说明:

对每个数据位置i, 分别寻找

   1. 以i为对称点的回文。比如文本: aba，以b对称。

   2. 以i与i+1直接的空隙对称的回文。比如文本abba，以bb之间的空隙对称。

所以，对每个点轮询两次。

回文算法: 马拉车(Manacher)算法

马拉车算法使用空间换取时间，把每个点的回文半径存储起来。为了避免轮询两次，算法把原始文本的每个字符让固定字符(比如#)前后包围起来，这样，对于原始文本aba和abba，处理后的文本变成#a#b#a#和#a#b#b#a#，这样，无论对于#a#b#a#和#a#b#b#a#，总有中心对称点m，从而避免了对称点落在字符的间隙中的情况。

算法把回文半径存储起来，在一个已经确定的大的回文当中，右半部分的点的回文与已经确定的左边部分的点回文具有对称性，所以节省掉一部分轮询的时间。这里说的某点的回文，指以该点为中心对称的回文。

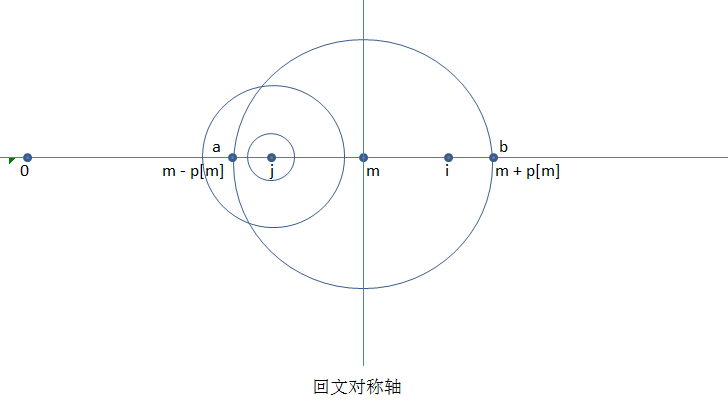
 如上图，以m点对称的回文其半径已经确定是p[m]，那么对于m点右侧的i点，总有一个沿m点对称的j点。由于m点回文的对称性，j点的回文与i点的回文在m回文的区域是一定对称的。这是马拉车算法规律的基础。

代码引用自: https://www.cnblogs.com/grandyang/p/4475985.html。源代码使用string和vector类，调试发现访问类中的数据是耗时的主要原因，所以将类数据改成更接近机器指令的数组，实测发现效率增长有百倍之多。这也是一个教训，评估算法不能通过高级的类去访问数据。

void Manacher(LPSTR s, int length_raw) {
    cout << "Manacher" << endl;
    
    int length = 2 * length_raw + 1;
    LPSTR t = new char[length + 1];
    for (int i = 0; i < length_raw; i ++) {
        t[2 * i] = '#';
        t[2 * i + 1] = s[i];
    }
    t[length - 1] = '#';
    t[length] = 0;

    int * p = new int[length];
    ZeroMemory(p, length * 4);
    __int64 start = get_local_ft_time();
    int mx = 0, id = 0, resLen = 0, resCenter = 0;
    for (int i = 1; i < length; ++i) {
        int p_i = mx > i ? min(p[2 * id - i], mx - i) : 1;
        while (t[i + p_i] == t[i - p_i]) ++p_i;
        if (mx < i + p_i) {
            mx = i + p_i;
            id = i;
        }
        if (resLen < p_i) {
            resLen = p_i;
            resCenter = i;
        }
        p[i] = p_i;
    }

    char c = s[(resCenter - resLen) / 2 + resLen - 1];
    s[(resCenter - resLen) / 2 + resLen - 1] = 0;
    cout << s + (resCenter - resLen) / 2 << endl;
    s[(resCenter - resLen) / 2 + resLen - 1] = c;
    __int64 end = get_local_ft_time();
    cout << "处理时间: " << diff_ft_time_ms(end, start)  << "ms" << endl;

    delete [] t;
    delete [] p;
}

回文算法: 自己尝试的算法

把文本数据看做函数曲线，则有下面的规律：

1. 递增或者递减的区间内，一定没有对称性。

    

2. 恒值区间，一定有对称性。

   

3. 递增、递减的属性变化时，在最高点或最低点(拐点)，可能存在对称性。

   

4. 递增或者递减变化成恒值时，一定没有对称性。

   

根据以上的规律，写出相应的代码：

void palindrome_zjs(LPSTR t, int length) {
    cout << "palindrome_zjs" << endl;
    __int64 start = get_local_ft_time();

    int l = 0;                                                    // 起点l(left，左边的意思)
    int s = 0;                                                    // 符号s(sign, 符号的意思)，代表上升，下降或者平坦 (1, -1, 0)
    int max = 0;                                                // 最长回文的起点
    int l_max = 1;                                                // 最长回文的长度(l: length, 长度的意思)
    for (int r = 1; r < length; r++) {                            // 终点r(right, 右边的意思)
        int s_n = t[r] == t[r - 1] ? 0 : t[r] > t[r - 1] ? 1 : -1;// 上升、下降或者不变?
        
        if (s_n == s) {                                            // 处在递增、递减或者恒值的阶段中，此时不作处理
            ;
        }
        else if(s_n == 0){                                        // 由递增、递减变成不变
            l = r - 1;                                            // 新线段的起点
            s = s_n;                                            // 增减属性
        }
        else if (s == 0) {                                        // 不变的区域结束。恒值区总是自对称，比如aa, aaa
            int i = 1;
            int right = r - 1;                                    // right指向最后一个恒值区的位置
            while (l - i >= 0 && right + i < length && 
                   t[l - i] == t[right + i]){                    // 沿恒值区向左右扩展即可。
                i++;
            }
            i--;                                                // 循环结束时i总不满足判断条件，所以减1
            if (right + i - (l - i) + 1 >  l_max){
                max   = l - i;
                l_max = right + i - max + 1;
            }
            l = r;                                                // 新线段的起点
            s = s_n;                                            // 增减属性
        }
        else if (s_n != 0) {                                    // 递增变成递减，或者递减变成递增
            int i = 1;
            int c = r - 1;                                        // c是拐点(最低或者最高点)。
            while (c - i >= 0 && c + i < length && t[c - i] == t[c + i]){        // 拐点为对称点。
                i++;
            }
            i--;                                                // i总不满足条件，所以减1
            if (2 * i + 1 > l_max){
                max   = c - i;
                l_max = 2 * i + 1;                                // + 1是加拐点本身
            }
            l = r;                                                // 新线段的起点
            s = s_n;                                            // 增减属性
        }
        assert(1);
    }

    char c = t[max + l_max];
    t[max + l_max] = 0;
    cout << t + max << endl;
    t[max + l_max] = c;
    __int64 end = get_local_ft_time();
    cout << "处理时间: " << diff_ft_time_ms(end, start)  << "ms" << endl;
}

几种算法的比较

算法　　　　　　格外的内存　　　运算时间(10M字节的随机文本)

原始算法　　　　不需要　　　　　30ms

马拉车算法　　　2倍的文本　　　 110ms

自己的代码　　　不需要　　　　　60ms

10M个数据，耗时在100ms左右(100M条指令)，算法的时间级数似乎都是O(n)。

结果颇让人费解，为什么马拉车算法和自己尝试的算法跑不过原始的算法?

我所能理解到的原因是这样的:

由于文本随机产生，产生长回文的可能性非常小，所以试图捕捉规律减少重复判断的那些代码的功效没有发挥出来。另一方面，由于考虑的更多，代码变复杂了，每个循环执行的指令条数就增加了，故而产生复杂算法跑不过原始算法的结果。

这里也验证了一个常识：代码越精简，执行指令条数越少，程序运行就越快。