什么是半平面交
- 一条有向直线会把平面分为两部分,若规定逆时针方向为正方向,则该有向直线逆时针方向的那一平面就是这条直线的半平面。
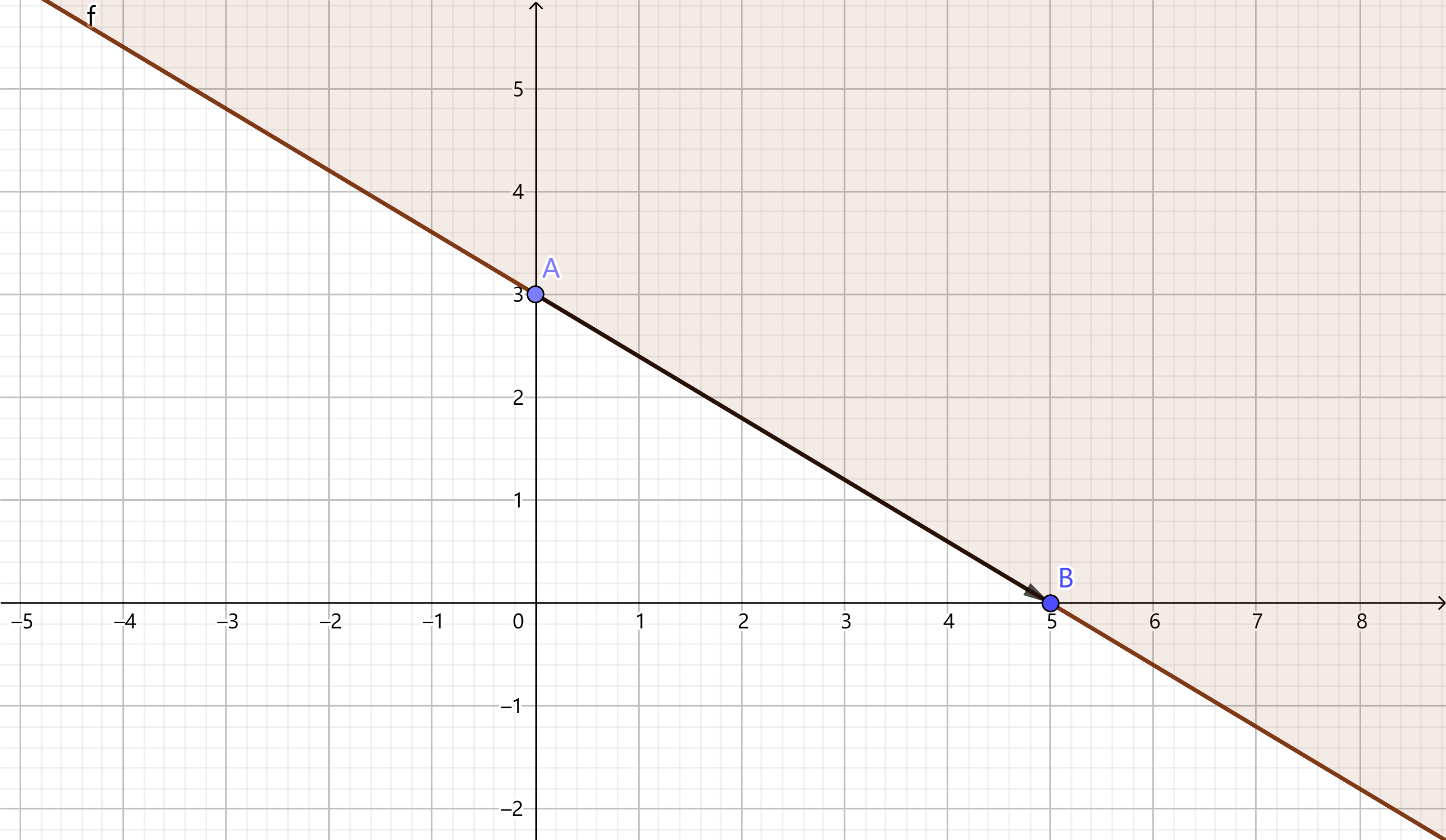
阴影部分就是这条直线的半平面。
- 而给出若干条有向直线并规定正方向以后,这些直线的半平面的交集就是这些直线的半平面交。
半平面交用来做什么
- 给出一个多边形,求它的核。核是该多边形内的一个凸多边形,核内的每个点都能看到多边形的每个角落。相当于核内任意一点与多边形上一点的连线都在多边形内。
形象的理解,多边形是一个房间,核是里面的一片区域,在这片区域里装摄像头,能监控到整个多边形。
半平面交的求法
只会S&I算法,当然这个算法也是最好的半平面交算法,好写,效率也很高。
计算几何基础
由于本人太菜了,需要总结一下计算几何基础。
直线表示
由于半平面交中直线是有向的,为了表示这样的直线,需要两个有序点对(s=(x1,y1), t=(x2,y2)),表示直线由(s)到(t)。此外半平面交中还需按极角排序,因此还需记录极角(一般规定极角为该直线正方向对应的射线与x轴正方向对应的射线的夹角)。
浮点比较
const eps = 1e-6;
int dcmp(double a, double b) { return fabs(a - b) < eps; }
直线交点
按照上面这种表示法,求两条直线的交点应该是这样的(cross是向量叉积):
POINT inter(LINE a, LINE b) { return a.s + (a.t - a.s) * (cross(b.t - b.s, a.s - b.s) / cross(a.t - a.s, b.t - b.s)); }
这个方法画图出来就很容易理解了。
在直线左or右
判断一个点是否在直线右边:
int onright(POINT a, LINE b) { return cross(b.t - b.s, a - b.s) < 0; }
利用了有向面积的正负性判断。
进入正题
S&I算法的大体步骤
- 将输入直线按照极角从小到大排序
Tips: 有些直线的极角大小是相等的,如果逆时针为正方向,那么显然位置较右的直线是没有用的,这时我们只保留最左边的直线。 - 开两个双端队列q1,q2,q1用来存半平面交上的直线,q2用来存半平面交上的点。
- 将第一条直线加入q1。
- 依次加入每条直线l[i],若q1中直线个数>1,则比较q2末尾的点是否在l[i]右边,是则弹出q1队尾的直线以及q2队尾的点,如此循环,直到不能删为止。
- 若q1中直线个数>1,则比较q2队头的点是否在l[i]右边,是则弹出q1队头的直线以及q2队头的点,如此循环,直到不能删为止。
- 将l[i]入队,算出l[i]与q1队尾直线的交点,将该交点加入q2队尾。
- 做完所有直线以后,检查q2队尾的点是否在q1队头直线右边,是则弹出q1队尾的直线以及q2队尾的点,如此循环,直到不能删为止。
- 检查q2队头的点是否在q1队尾直线右边,是则弹出q1队头的直线以及q2队头的点,如此循环,直到不能删为止。
- 此时q1中的直线即为半平面交的每条边,q2即为半平面交上的点(还要加上最后加入的直线与最早加入的直线的交点)。
流程解释
- 为什么要排序?
排序后我们就是在逆时针地加入每条直线,这样直线间关系就存在了单调性,保证了后面过程的正确性。 - 为什么要用双端队列?
因为求半平面交的过程实际上是环形的,新加入的直线不仅会影响到最后加入的直线,也会影响到最早加入的直线。
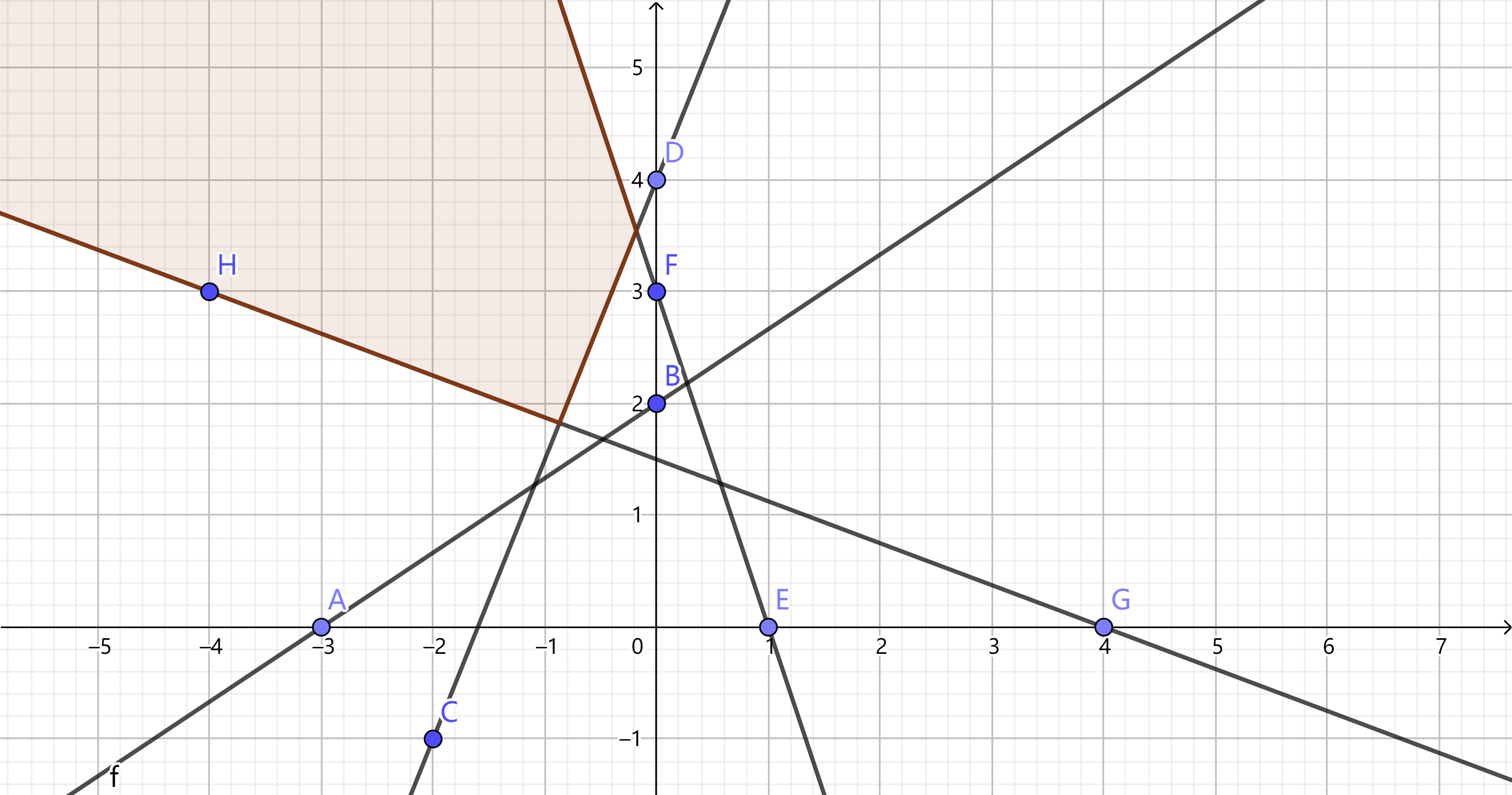
依次加入直线AB,直线CD,直线EF,直线HG
AB,CD的交点在HG右侧,那么此时最早加入的直线AB已无用处,将它出队。
代码
poj3130 判断多边形是否有核
#include <cmath>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef double db;
const int N = 57;
const db eps = 1e-6;
int dcmp(db a, db b) { return fabs(a - b) < eps; } //浮点数比较相等
struct VECTOR
{
db x, y;
VECTOR(db X = 0, db Y = 0) { x = X, y = Y; }
db getang() { return atan2(y, x); } //求极角
};
db cross(VECTOR a, VECTOR b) { return a.x * b.y - a.y * b.x; } //叉积
VECTOR operator+(VECTOR a, VECTOR b) { return VECTOR(a.x + b.x, a.y + b.y); } //基本向量运算
VECTOR operator-(VECTOR a, VECTOR b) { return VECTOR(a.x - b.x, a.y - b.y); }
VECTOR operator*(VECTOR a, db b) { return VECTOR(a.x * b, a.y * b); }
typedef VECTOR POINT;
struct LINE
{
POINT s, t;
db ang;
LINE() {}
LINE(POINT S, POINT T) { s = S, t = T, ang = (t - s).getang(); } //根据起点终点构造直线
};
int operator<(LINE a, LINE b) { return dcmp(a.ang, b.ang) ? cross(b.t - a.s, a.t - a.s) + eps > 0 : a.ang < b.ang; } //比较极角,极角相等时保证最左边的直线排的最前
POINT inter(LINE a, LINE b) { return a.s + (a.t - a.s) * (cross(b.t - b.s, a.s - b.s) / cross(a.t - a.s, b.t - b.s)); } //计算两直线的交点
int onright(POINT a, LINE b) { return cross(b.t - b.s, a - b.s) < 0; } //判断一个点是否在某直线右边
int n;
POINT p[N];
LINE l[N];
int h, t;
LINE q1[N];
POINT q2[N];
int SI()
{
sort(l + 1, l + n + 1); //排序
h = 1, q1[t = 1] = l[1];
for (int i = 2; i <= n; i++)
{
if (dcmp(l[i].ang, l[i - 1].ang)) continue; //多条极角相同的直线,取最左边的一条
while (h < t && onright(q2[t - 1], l[i])) t--; //删掉队尾无用直线
while (h < t && onright(q2[h], l[i])) h++; //删掉队头无用直线
q1[++t] = l[i];
if (h < t) q2[t - 1] = inter(q1[t], q1[t - 1]); //加入交点
}
while (h < t && onright(q2[t - 1], q1[h])) t--; //最后检查
while (h < t && onright(q2[h], q1[t])) h++;
if (t - h <= 1) return 0; //半平面交上的点少于3个,无法构成多边形,该多边形的核不存在
return 1;
}
int main()
{
while (1)
{
scanf("%d", &n);
if (!n) break;
for (int i = 1; i <= n; i++) scanf("%lf%lf", &p[i].x, &p[i].y);
l[1] = LINE(p[n], p[1]); //输入保证该线段左侧是多边形的内部,直接连线即可
for (int i = 2; i <= n; i++) l[i] = LINE(p[i - 1], p[i]);
printf(SI() ? "1
" : "0
");
}
return 0;
}